专栏文章

题解：P3006 [USACO11JAN] Bottleneck G

__lqs_
P3006题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mio7eo65
此快照首次捕获于
2025/12/02 14:35
3 个月前
此快照最后确认于
2025/12/02 14:35
3 个月前
查看原文
比较容易使人思维弄混的一个题。
贪心策略肯定对于任意一个点，只要能往上跑就往上跑，也就是尽量让每一条边都满流。这样直接模拟的话是 O(n2qt)O(n^2qt) 或者 O(nqt)O(nqt)。
但复杂度肯定不可能带 tt，考虑怎么先把 tt 去掉。可以设计一个简单的树形 dp：设 fuf_{u} 表示 tt 秒内经过点 uu 流向父亲的最大数量。那么显然有 fu=min⁡(t×mu,(∑v∈sonufv)+cu)f_{u}=\min(t \times m_u,(\sum\limits_{v \in son_u} f_v)+c_u)。这样可以做到 O(nq)O(nq)。
由于这个树形 dp 依赖于 tt 的具体值，因此这个做法无法优化。但得到的一个启示是可以往流入流出的方向想。对于一个点 uu，如果 mu>∑mvm_u > \sum\limits m_v，那么总有一个时刻 tt 使得原来在 uu 处的牛都流出了，t+1t+1 之后的时刻一定是 vv 流向 uu 再流向 faufa_u，因为点 uu 入不敷出，根据一开始的贪心策略肯定会再往上流，相当于这个 uu 没有用了。那么我们设 gug_{u} 表示这个出入关系，则 gu=mu−∑mvg_u=m_u-\sum\limits m_v。那么若 gug_u 为正，则当 t>cugut > \dfrac{c_u}{g_u} 时 uu 就相当于一个中转点要将儿子的流量流向父亲。
然后我们考虑一个这样的树：
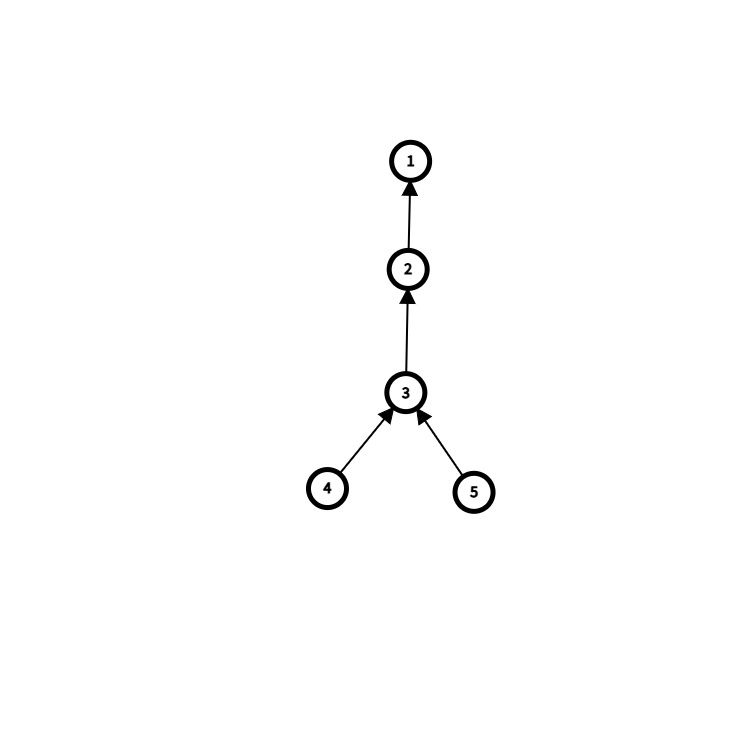
很明显在二号点出现“入不敷出”的情况之前，11 号点最终的数量只和 m2m_2 有关，因为一直是满流。但实际情况可能是来自 345 的流向了 1。但这并不重要，因为我们只关心流了多少而不是来自哪里。当 2 号点不够了之后，实际就是全部的流入都来自 345，相对应的单位时间的流入大小也有改变。那么怎么维护这个信息呢？可以直接把 345 直接连向 1 号点，然后把他们的流量信息合并到 1 号点，这一过程可以并查集维护。
更一般地，若 t>cugut > \dfrac{c_u}{g_u}，我们把点 uu 并到父亲所在集合的根那里去，然后令 cfau←cfau+cu,gfau←gfau+guc_{fa_u} \leftarrow c_{fa_u}+c_u,g_{fa_u} \leftarrow g_{fa_u}+g_u。等价于所有儿子直接流向 uu 的父亲，且之前流到 uu 的都流走了。然后我们需要重新计算新合并的点再次“入不敷出”的时间 t′t'。需要注意的是，这里的 faufa_u 并非是 uu 的父亲节点，而是并查集 find 函数找 uu 父亲所在的根节点。
通过干这样一件事情，我们保证了当前所有节点都会进行下一次流出（除非已经全部流到 11 号点）。然后小根堆维护一下时间，将询问离线后排序，把经过的时间点依次合并。这样就实时地维护了每个时间点流向 11 号点的流量。因此答案为 c1−g1×tc_1-g_1 \times t，其中 tt 是当前询问的时间，g1g_1 是负的所以要减。
复杂度是 O((n+q)log⁡n)O((n+q) \log n)，感觉这个题理解起来还是挺抽象的。
代码：
CPP
#include<bits/stdc++.h>
using namespace std;
#define N 200005
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
int n,i,j,ans,k,Q,t,s,m[N],c[N],p[N],g[N],res[N];
std::priority_queue<pii>q;
struct ren{
	int t,w;
	bool operator < (const ren &A) const{
		return t < A.t; 
	}
}d[N];
struct DSU{
	int f[N];
	void init(){
		for(int i=1;i<=n;i++) f[i]=i; 
		return;
	}
	int find(int x){
		if(x==f[x]) return x;
		return f[x]=find(f[x]);
	}
}dsu;
signed main(){
	scanf("%lld%lld",&n,&Q);
	for(i=2;i<=n;i++){
		scanf("%lld%lld%lld",&p[i],&c[i],&m[i]);
		g[p[i]]-=m[i],g[i]+=m[i],s+=c[i];
	}
	for(i=1;i<=n;i++){
		if(g[i]>0) q.push({-c[i]/g[i],i});
	}
	for(i=1;i<=Q;i++) scanf("%lld",&d[i].t),d[i].w=i;
	sort(d+1,d+1+Q);
	dsu.init();
	for(i=1;i<=Q;i++){
		while(!q.empty() && -q.top().fi<d[i].t){//只能< 
			int x=q.top().se;
			q.pop();		
			if(dsu.f[x]!=x) continue;
			int k=dsu.find(p[x]);
			g[k]+=g[x],c[k]+=c[x],dsu.f[x]=k;
			if(g[k]>0) q.push({-c[k]/g[k],k});
		}
		res[d[i].w]=min(s,c[1]-g[1]*d[i].t);
	}
	for(i=1;i<=Q;i++) printf("%lld\n",res[i]);
	return 0;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...