专栏文章
Lomost gelral的另类解法
CF600E题解参与者 2已保存评论 2
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 2 条
- 当前快照
- 1 份
- 快照标识符
- @mintjyxo
- 此快照首次捕获于
- 2025/12/02 08:07 3 个月前
- 此快照最后确认于
- 2025/12/02 08:07 3 个月前
Lomsat gelral
题意:
- 求以 为根时,每个子树中出现次数最多的颜色编号之和。
方法:
一些与其他人完全不一样的实现思路:
因为编号之和及其难以维护(或者有大佬用分治写???)并且查询离线,考虑使用 dsu on tree,即树上启发式合并。
如何想到 dsu on tree 其实是其他题解都已经讲烂了的东西,但本文的重点不是这个。本文主要想介绍一种 dsu on tree 的实现思路:
先对这棵树重链剖分,仅对链顶建立 map 储存颜色个数。对于每一个节点,继承它的重儿子统计的答案,再对轻儿子暴力统计答案。由于一个节点的轻儿子一定是一个重链的链顶,所以在递归处理完轻儿子时,它的答案一定存储在它本身的位置上。
这样用文字讲解可能有一些抽象,所以我们可以再次用图片与例子讲解一下。
有树如下:
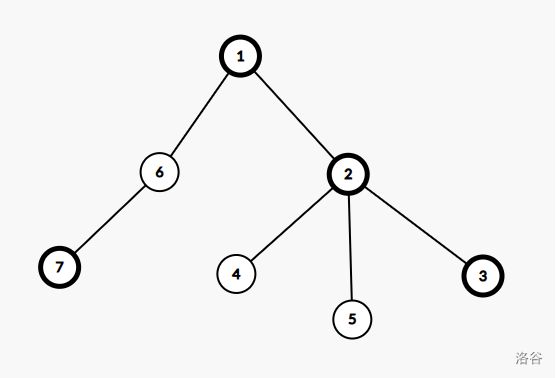
则标黑的节点便是为他父亲的重儿子(图的标注节点 不是重儿子,因为它是根节点)。
在这棵树中,我们仅在 节点建立 map,其余节点与他所在链的链顶节点共享一个 map。
又对于每一个节点,用 统计当前 节点子树中个数最多的颜色的编号和, 统计出现个数最多颜色的出现次数。
在递归处理中,先递归重儿子,将重儿子所对应的答案储存在链顶的 map 中,如下图(以 节点为例):
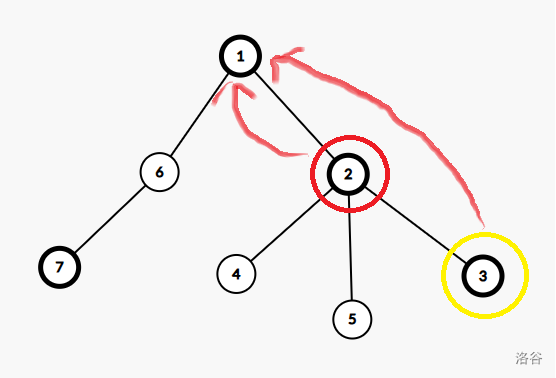
因为 节点与 节点共用位子在 的 map,继承这步操作便只需要将 ,。
在暴力合并 4,5 节点时,直接在存储 2 子树答案的 map 中查找每一个在 4 中的答案,直接修改。
代码实现长这样:
CPPfor( map< int , int >::iterator it = a[ son[ i ] ].begin() ; it != a[ son[ i ] ].end( ) ; it ++ )
{
insert( it->first , id , it -> second ) ;
judge( now_data , a[ id ][ it -> first ] , it -> first ) ;
}
在大佬的帮助下,空间复杂度的证明也是成功的写出来了:


总体代码:
CPP#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 1e5 + 10 ;
int title[ N ] , tot = 0 ;
int siz[ N ] , max_son[ N ] ;
map< int , int > a[ N ] ;
pair< int , int > ans[ N ] ;
int input[ N ] , n , m ;
struct node
{
int data ;
int next;
}edge[ N << 1 ] ;
void add( int x , int y )
{
edge[ ++ tot ].data = y ;
edge[ tot ].next = title[ x ] ;
title[ x ] = tot ;
}
void judge( int now_data , int sum , int color )
{
if( ans[ now_data ].second == sum )
{
ans[ now_data ].first += color ;
}
else if( ans[ now_data ].second > sum ) return ;
else
{
ans[ now_data ].first = color , ans[ now_data ].second = sum ;
}
}
void insert( int color , int id , int siz )
{
auto it = a[ id ].find( color ) ;
if( it != a[ id ].end() )
it->second = a[ id ][ color ] + siz ;
else a[ id ][ color ] = siz ;
}
void dfs( int now_data , int from_data )
{
siz[ now_data ] = 1 ;
for( int i = title[ now_data ] ; i != -1 ; i = edge[ i ].next )
{
if( edge[ i ].data == from_data ) continue ;
dfs( edge[ i ].data , now_data ) ;
siz[ now_data ] += siz[ edge[ i ].data ] ;
if( siz[ edge[ i ].data ] > siz[ max_son[ now_data ] ] ) max_son[ now_data ] = edge[ i ].data ;
}
}
void dfs1( int now_data , int from_data , int id )
{
vector< int > son ;
if( max_son[ now_data ] == 0 )
{
insert( input[ now_data ] , id , 1 ) ;
judge( now_data , a[ id ][ input[ now_data ] ] , input[ now_data ] ) ;
return ;
}
dfs1( max_son[ now_data ] , now_data , id ) ;
ans[ now_data ] = ans[ max_son[ now_data ] ] ;
for( int i = title[ now_data ] ; i != -1 ; i = edge[ i ].next )
{
if( edge[ i ].data == from_data || edge[ i ].data == max_son[ now_data ] ) continue ;
dfs1( edge[ i ].data , now_data , edge[ i ].data ) ;
son.push_back( edge[ i ].data ) ;
}
insert( input[ now_data ] , id , 1 ) ;
judge( now_data , a[ id ][ input[ now_data ] ] , input[ now_data ] ) ;
for( int i = 0 ; i < ( int ) son.size( ) ; i ++ )
{
for( map< int , int >::iterator it = a[ son[ i ] ].begin() ; it != a[ son[ i ] ].end( ) ; it ++ )
{
insert( it->first , id , it -> second ) ;
judge( now_data , a[ id ][ it -> first ] , it -> first ) ;
}
}
}
signed main()
{
memset( title , -1 , sizeof title ) ;
cin >> n ;
for( int i = 1 ; i <= n ; i ++ ) cin >> input[ i ] ;
for( int i = 2 ; i <= n ; i ++ )
{
int x , y ;
cin >> x >> y ;
add( x , y ) ;
add( y , x ) ;
}
dfs( 1 , 1 ) ;
dfs1( 1 , 1 , 1 ) ;
for( int i = 1 ; i <= n ; i ++ ) cout << ans[ i ].first << " " ;
return 0 ;
}
再此,致谢大佬 wing_heart!!!
相关推荐
评论
共 2 条评论,欢迎与作者交流。
正在加载评论...