专栏文章

题解：P14376 [JOISC 2018] 野猪 / Wild Boar

cchenbs
P14376题解参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@min4y7y4
此快照首次捕获于
2025/12/01 20:38
3 个月前
此快照最后确认于
2025/12/01 20:38
3 个月前
查看原文

暴力

直接贪心显然是假的，因为不能往回走。考虑 DP，设 fi,jf_{i,j} 表示走到了第 XiX_i，上一条边是 jj 的最优解。
考虑怎么从 fi−1,jf_{i-1,j} 转移到 fi,kf_{i,k}，可以枚举 Xi−1X_{i-1} 的出边 e≠je \neq j，然后删掉 XiX_i 周围除了 kk 以外的边，从 ee 的另一端开始跑最短路，最短路的时候记录上一条边防止往回走。
时间复杂度应该是 O(TLM3log⁡M)O(TL M^3 \log M)。

改进的暴力

考虑怎么优化，注意到两个点之间的很多路径都没用，我们可以先找出每个点对 (a,b)(a,b) 之间的少量关键路径，然后转移的时候直接枚举关键路径即可。
找出的关键路径需要满足以下条件：
  • 在与 aa 连接的边中任意规定一条不能作为路径开头、在与 bb 连接的边中任意规定一条不能作为路径末尾，(a,b)(a,b) 间的最短路径都是关键路径。
下面分析怎么找出这样的路径，方法可能不唯一。
首先容易找出 (a,b)(a,b) 点对之间的最短路和次短路作为前两条关键路径。这里的次短路要求开头或者结尾与最短路不同。然后根据这两条路径的形态分类讨论：
若两条路径在开头重合，如下图：
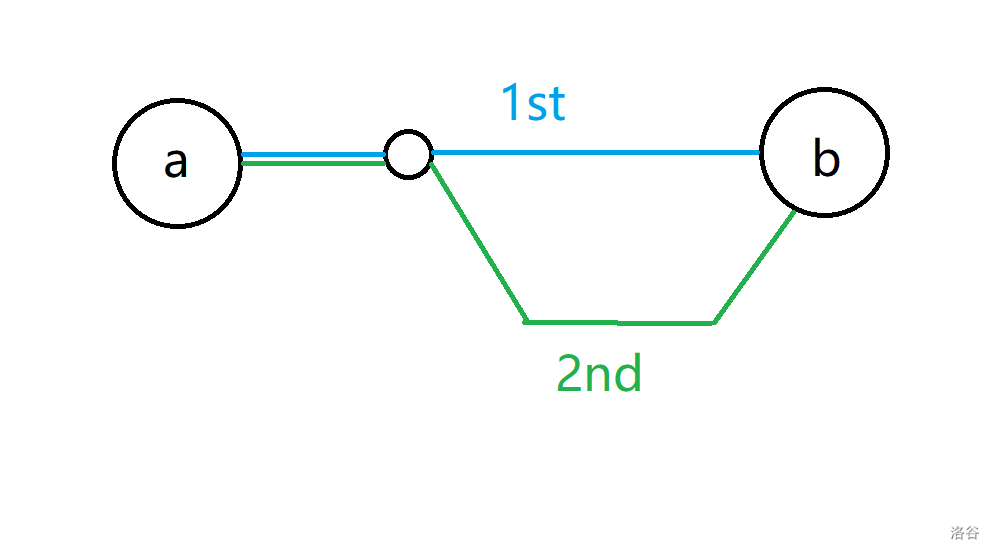
记重合的这条边为 ee，则需要再补充两条开头不为 ee、结尾不同的路径，就可以满足上述的条件：
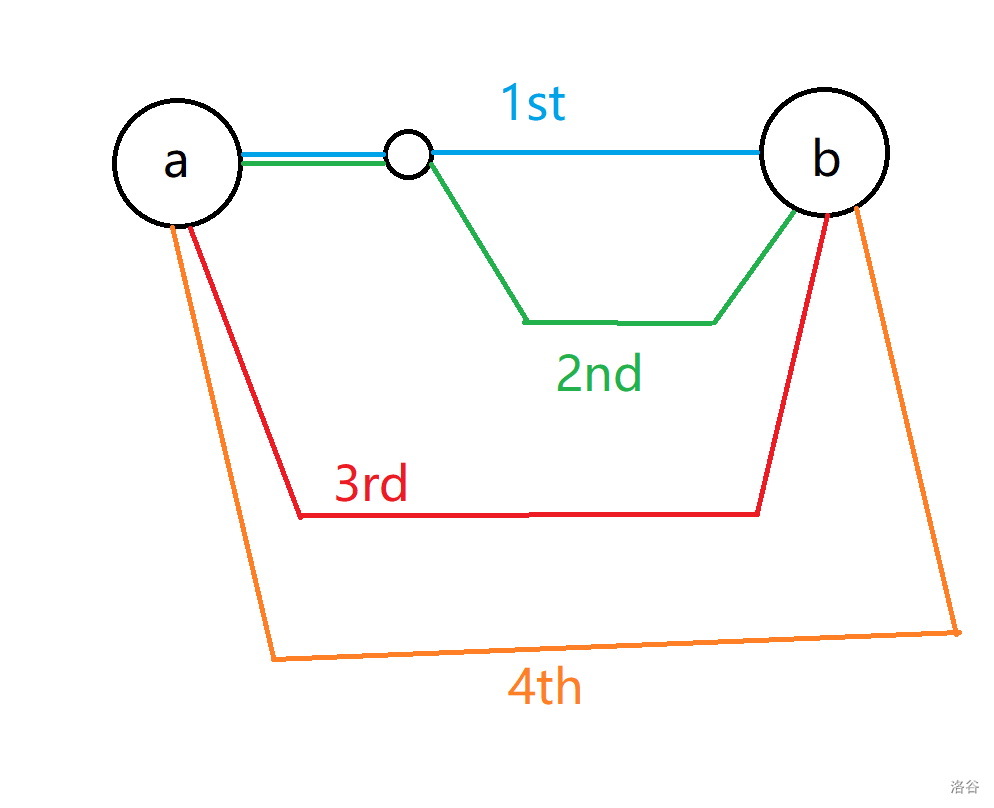
注意，上图中，33、44 两条路径的开头重合也没关系，结尾必须不同。
若两条路径在结尾重合也是同理的。
若两条路径不重合，就再补充一条开头与路径 11 不同，结尾与路径 22 不同的路径，和一条开头与路径 22 不同，结尾与路径 11 不同的路径，从而覆盖各种情况。
时间复杂度 O(M2log⁡M+TL)O(M^2 \log M + TL) 带上超级大常数。

正解

注意到两组关键路径可以合并，用线段树维护即可（线段树每个节点记录四条路径）。
时间复杂度变成了 O(M2log⁡M+Tlog⁡L)O(M^2 \log M + T \log L) 带上超级大常数，1010 秒时限可以轻松通过。
注：我记录前驱时，存的是边的序号，因为我没仔细看条件，以为有重边。
CPP
#include<bits/stdc++.h>
using namespace std;
int n,m,t,l,x[100005];
struct eg {
	int u,v,w;
} e[2005];
vector<int> G[2005];
typedef pair<long long,int> pli;
int vis[2005];
long long f[100005][505];
const long long inf=5e17;
pli dis[2005][2005][2]; // 从第 i 条出边出去，到 j 的最短路/次短路
priority_queue<pli,vector<pli>,greater<pli> > pq;
struct path {
	int st, ed; // 边的序号
	long long len=inf;
};
inline void cmin(path &x, path y) {
	if(y.len<x.len) x=y;
}
array<path,4> rem[2005][2005];
class SGT {
		array<path,4> merge(array<path,4> x, array<path,4> y) {
			path tmp[16];
			int tot=0;
			for(int i=0; i<4; i++)
				for(int j=0; j<4; j++)
					if(x[i].ed!=y[j].st)
						tmp[tot++]= {x[i].st,y[j].ed,x[i].len+y[j].len};
			array<path,4> z;
			for(int i=0; i<tot; i++) cmin(z[0],tmp[i]);
			for(int i=0; i<tot; i++)
				if(tmp[i].st!=z[0].st || tmp[i].ed!=z[0].ed)
					cmin(z[1],tmp[i]);
			if(z[0].st==z[1].st) {
				for(int i=0; i<tot; i++) if(tmp[i].st!=z[0].st) cmin(z[2],tmp[i]);
				for(int i=0; i<tot; i++)
					if(tmp[i].st!=z[0].st && tmp[i].ed!=z[2].ed) cmin(z[3],tmp[i]);
			} else if(z[0].ed==z[1].ed) {
				for(int i=0; i<tot; i++) if(tmp[i].ed!=z[0].ed) cmin(z[2],tmp[i]);
				for(int i=0; i<tot; i++)
					if(tmp[i].st!=z[2].st && tmp[i].ed!=z[0].ed) cmin(z[3],tmp[i]);
			} else {
				for(int i=0; i<tot; i++) if(tmp[i].st!=z[0].st && tmp[i].ed!=z[1].ed) cmin(z[2],tmp[i]);
				for(int i=0; i<tot; i++) if(tmp[i].st!=z[1].st && tmp[i].ed!=z[0].ed) cmin(z[3],tmp[i]);
			}
			return z;
		}
	public:
		array<path,4> t[400005];
		void build(int u, int l, int r) {
			if(l==r) {
				t[u]=rem[x[l]][x[l+1]];
				return;
			}
			int mid=l+r>>1;
			build(u<<1,l,mid);
			build(u<<1|1,mid+1,r);
			t[u]=merge(t[u<<1],t[u<<1|1]);
		}
		void modify(int u, int l, int r, int x, array<path,4> y) {
			if(l==r) {
				t[u]=y;
				return;
			}
			int mid=l+r>>1;
			if(x<=mid) modify(u<<1,l,mid,x,y);
			else modify(u<<1|1,mid+1,r,x,y);
			t[u]=merge(t[u<<1],t[u<<1|1]);
		}
		long long query() {
			return t[1][0].len>=inf ? -1 : t[1][0].len;
		}
} sgt;
void findpath(int a, int b, int ban1, int ban2, path &out) {
	for(int i=0; i<G[a].size(); i++) {
		if(G[a][i]==ban1) continue;
		for(int j=0; j<=1; j++) {
			if(dis[i][b][j].second==ban2) continue;
			cmin(out, {G[a][i], dis[i][b][j].second, dis[i][b][j].first});
		}
	}
}
int main() {
	cin>>n>>m>>t>>l;
	for(int i=1; i<=m; i++) {
		cin>>e[i].u>>e[i].v>>e[i].w;
		G[e[i].u].push_back(i);
		G[e[i].v].push_back(i);
//		assert(e[i].u!=e[i].v);
	}
	for(int i=1; i<=n; i++) {
		for(int j=0; j<G[i].size(); j++) {
			for(int p=1; p<=n; p++) dis[j][p][0].first=dis[j][p][1].first=inf;
			int x=G[i][j], k=e[x].u^e[x].v^i;
			// 最短路
			memset(vis,0,sizeof vis);
			pq.push({e[x].w, k}), dis[j][k][0] = {e[x].w,x};
			while(!pq.empty()) {
				int cur=pq.top().second;
				pq.pop();
				if(vis[cur]) continue;
				vis[cur]=1;
				for(auto p:G[cur]) {
					int to=e[p].u^e[p].v^cur;
					if(p==dis[j][cur][0].second) continue;
					if(dis[j][to][0].first > dis[j][cur][0].first+e[p].w) {
						dis[j][to][0] = {dis[j][cur][0].first+e[p].w, p};
						pq.push({dis[j][to][0].first, to});
					}
				}
			}
			// 次短路
			for(int p=1; p<=n; p++) {
				for(auto q:G[p]) {
					int to=e[q].u^e[q].v^p;
					if(q==dis[j][to][0].second) continue; // 不能留在最短路上
					if(q==dis[j][p][0].second) continue; // 不能往回走
					if(dis[j][to][1].first > dis[j][p][0].first+e[q].w) {
						dis[j][to][1] = {dis[j][p][0].first+e[q].w,q};
					}
				}
			}
			memset(vis,0,sizeof vis);
			for(int p=1; p<=n; p++) pq.push({dis[j][p][1].first, p});
//			printf("i=%d j=%d:\n",i,j);
//			for(int p=1; p<=n; p++)
//				printf("(%lld,%d) (%lld,%d)\n",dis[j][p][0].first,dis[j][p][0].second,dis[j][p][1].first,dis[j][p][1].second);

			while(!pq.empty()) {
				int cur=pq.top().second;
				pq.pop();
				if(vis[cur]) continue;
				vis[cur]=1;
				for(auto p:G[cur]) {
					int to=e[p].u^e[p].v^cur;
					if(p==dis[j][to][0].second) continue; // 不能回到最短路上
					if(p==dis[j][cur][1].second) continue;
					if(dis[j][to][1].first > dis[j][cur][1].first+e[p].w) {
						dis[j][to][1] = {dis[j][cur][1].first+e[p].w, p};
						pq.push({dis[j][to][1].first, to});
					}
				}
			}
//			printf("i=%d j=%d:\n",i,j);
//			for(int p=1; p<=n; p++)
//				printf("(%lld,%d) (%lld,%d)\n",dis[j][p][0].first,dis[j][p][0].second,dis[j][p][1].first,dis[j][p][1].second);
		}
		for(int j=1; j<=n; j++) {
			for(int k=0; k<G[i].size(); k++)
				cmin(rem[i][j][0], {G[i][k], dis[k][j][0].second, dis[k][j][0].first});
			for(int k=0; k<G[i].size(); k++)
				for(int p=0; p<=1; p++)
					if(G[i][k]!=rem[i][j][0].st || dis[k][j][p].second!=rem[i][j][0].ed)
						cmin(rem[i][j][1], {G[i][k], dis[k][j][p].second, dis[k][j][p].first});
			if(rem[i][j][0].st==rem[i][j][1].st) {
				findpath(i,j,rem[i][j][0].st,-1,rem[i][j][2]);
				findpath(i,j,rem[i][j][0].st,rem[i][j][2].ed,rem[i][j][3]);
			} else if(rem[i][j][0].ed==rem[i][j][1].ed) {
				findpath(i,j,-1,rem[i][j][0].ed,rem[i][j][2]);
				findpath(i,j,rem[i][j][2].st,rem[i][j][0].ed,rem[i][j][3]);
			} else {
				findpath(i,j,rem[i][j][0].st,rem[i][j][1].ed,rem[i][j][2]);
				findpath(i,j,rem[i][j][1].st,rem[i][j][0].ed,rem[i][j][3]);
			}
		}
	}
	for(int i=1; i<=l; i++) cin>>x[i];
	sgt.build(1,1,l-1);
	for(int i=1; i<=t; i++) {
		int p,q;
		cin>>p>>q;
		x[p]=q;
		if(p!=l) sgt.modify(1,1,l-1,p,rem[x[p]][x[p+1]]);
		if(p!=1) sgt.modify(1,1,l-1,p-1,rem[x[p-1]][x[p]]);
		cout<<sgt.query()<<'\n';
	}
	return 0;
}

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...