专栏文章

线段树

DDJ_Liu
算法·理论参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@min9ufbh
此快照首次捕获于
2025/12/01 22:55
3 个月前
此快照最后确认于
2025/12/01 22:55
3 个月前
查看原文
线段树一个接一个的向我们走来了...
目标：一天补充一个知识点（

普通线段树

线段树本质上并非维护线段的树，而是一个将大区间连向它的两个小子区间的树，每个节点都是一个区间，可以高效的解决一类维护区间信息的问题
先来看看基本结构：
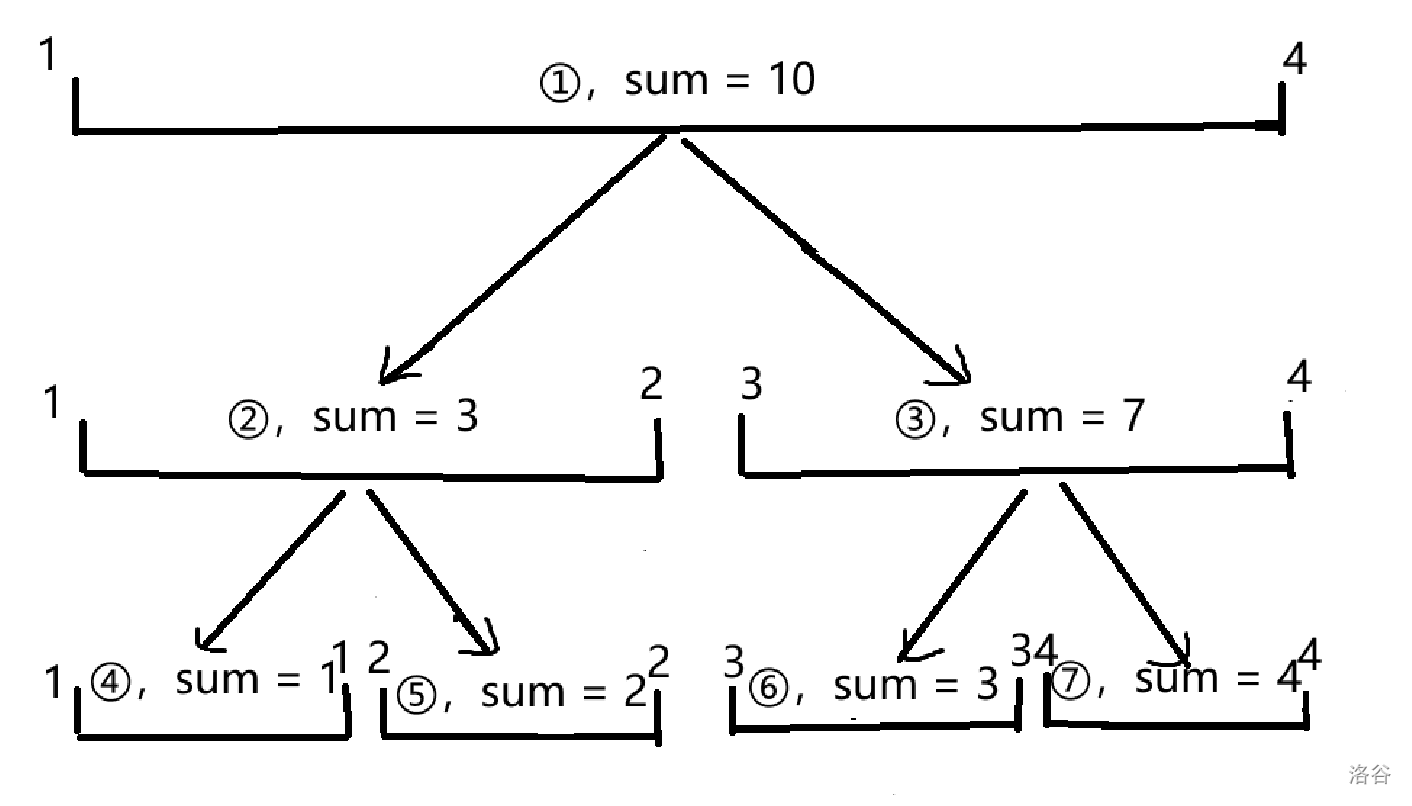
所以线段树算是一个二叉搜索树（？
我们注意到每一层的区间答案都可以由它下面一层的两个询问合并得到，编号正好是自身的两倍和两倍加一，这就是线段树的关键思想
怎么建这棵线段树呢
从满区间出发，依次分成左右两个区间递归，直到长度为 1 时就是数组的那一位，随后再由左右两个区间合并得到这个区间的答案，很明显它最多只有 O(log⁡n)O(\log n) 次递归
code（以求和为例）:
CPP
#define ls (x << 1) // 左区间编号
#define rs (ls + 1) // 右区间编号
#define mid ((l + r) >> 1) // 区间中点
void pushup(int x) { t[x] = t[ls] + t[rs]; } // 本区间 = 左区间 + 右区间
// t数组是每个节点对应的区间的答案
void build(int x, int l, int r) {
    // 当前访问到 x 节点，对应的区间是 [l, r]
    if (l == r) t[x] = a[l];
    else {
        build(ls, l, mid);
        build(rs, mid + 1, r);
        pushup(x);
    }
}

单修区查

单点修改是比较容易的，每次递归判断一下它在mid左边还是右边，递归到最底层修改即可，注意最后还是要pushup算上面每个区间的贡献，每次都是 O(log⁡n)O(\log n) 的
code（单点加）:
CPP
// 在位置 p 加上 k
void upd(int x, int l, int r, int p, int k) {
    if (l == r) t[p] += k;
    else {
        if (p <= mid) upd(ls, l, mid, q, k);
        else upd(rs, mid + 1, r, q, k);
        pushup(x);
    }   
}
区间查询一样，比如你要查询 [1,3][1, 3]，从上往下递归，首先发现 [1,3][1, 3] 跨过了 [1,4][1, 4] 的中点，所以同时计算两边，即 [1,2][1, 2] 和 [3,4][3, 4]。而这时 [1,2][1, 2] 刚好在 [1,3][1, 3] 内部，直接算入贡献，[3,4][3, 4] 继续递归分成 [3,3][3, 3] 和 [4,4][4, 4]，这时 [3,3][3, 3] 也完全被 [1,3][1, 3] 包含了，算入贡献，结束。可以发现最多需要访问 O(log⁡n)O(\log n) 个区间。
code（区间求和）:
CPP
// 查询 [ml, mr] 的总和
int qry(int x, int l, int r, int ml, int mr) {
    // 判断是否包含
    if (ml <= l && r <= mr) return t[x];
    else {
        int ans = 0;
        if (ml <= mid) (ans += qry(ls, l, mid, ml, mr)) %= mod;
        if (mr > mid) (ans += qry(rs, mid + 1, r, ml, mr)) %= mod;
        return ans;
    }  
}
这里的 ml,mrml, mr 是询问的区间

区修区查

上面的做法在区间修改上会炸成 O(n)O(n)，于是便诞生了懒标记的神奇玩意
懒标记就是在每个节点受到修改的时候不直接往下递归子区间的修改，而是先保留下来，直到要访问子区间的时候再下传标记，从而在保证正确的情况下减少复杂度
看代码吧：
CPP
void upd(int x, int l, int r, int ml, int mr, int k) {
    // 判断是否包含
    if (ml <= l && r <= mr) t[x] += (r - l + 1) * k, lz[x] += k; // lz 就是懒标记数组
    else {
        pushdown(x, l, r); // 懒标记下传
        // 因为要递归子区间所以要下传
        if (ml <= mid) upd(ls, l, mid, ml, mr, k);
        if (mr > mid) upd(rs, mid + 1, r, ml, mr, k);
        pushup(x);
    }   
}
int qry(int x, int l, int r, int ml, int mr) {
    if (ml <= l && r <= mr) return t[x];
    else {
        pushdown(x, l, r);
        // 同理，下面要递归子区间了
        int ans = 0;
        if (ml <= mid) (ans += qry(ls, l, mid, ml, mr)) %= mod;
        if (mr > mid) (ans += qry(rs, mid + 1, r, ml, mr)) %= mod;
        return ans;
    }  
}
下传标记是一个很重要的点，不过也不难，让大区间的左右区间加上大区间的懒标记，同时在左右区间的懒标记也要加上大区间的，这样大区间的懒标记结束了它的使命，可以清零了
code:
CPP
void pushdown(int x, int l, int r) {
    t[ls] += lz[x] * (mid - l + 1);
    t[rs] += lz[x] * (r - mid); // 子区间答案修改
    lz[ls] += lz[x], lz[rs] += lz[x]; // 子区间懒标记修改
    lz[x] = 0; // 本区间懒标记清零
}
哦对，线段树要开 4 倍空间，具体为什么你不用管
放一个完整的区修区查代码：
CPP
struct seg {
    int t[maxn << 2], lz[maxn << 2];
    #define ls (x << 1)
    #define rs (ls + 1)
    #define mid ((l + r) >> 1)
    void pushup(int x) { t[x] = (t[ls] + t[rs]) % mod; }
    void pushdown(int x, int l, int r) {
        (t[ls] += lz[x] * (mid - l + 1)) %= mod;
        (t[rs] += lz[x] * (r - mid)) %= mod;
        (lz[ls] += lz[x]) %= mod, (lz[rs] += lz[x]) %= mod;
        lz[x] = 0;
    }
    void build(int x, int l, int r) {
        if (l == r) t[x] = a[l];
        else {
            build(ls, l, mid);
            build(rs, mid + 1, r);
            pushup(x);
        }
    }
    void upd(int x, int l, int r, int ml, int mr, int k) {
        if (ml <= l && r <= mr) (t[x] += (r - l + 1) * k) %= mod, (lz[x] += k) %= mod;
        else {
            pushdown(x, l, r);
            if (ml <= mid) upd(ls, l, mid, ml, mr, k);
            if (mr > mid) upd(rs, mid + 1, r, ml, mr, k);
            pushup(x);
        }   
    }
    int qry(int x, int l, int r, int ml, int mr) {
        if (ml <= l && r <= mr) return t[x];
        else {
            pushdown(x, l, r);
            int ans = 0;
            if (ml <= mid) (ans += qry(ls, l, mid, ml, mr)) %= mod;
            if (mr > mid) (ans += qry(rs, mid + 1, r, ml, mr)) %= mod;
            return ans;
        }  
    }
} t;
模板：P3372 【模板】线段树 1
代码上面给了

动态开点

如果总长度特别大的话，普通线段树肯定会炸空间，这时候就要用到动态开点线段树了
具体来说就是在访问到这个节点的时候在新建这个节点，所以这样最多只会有 O(mlog⁡n)O(m\log n) 个点，mm 是操作数
因为每个节点都是单开的，我们不能直接得到左右区间的编号，应该用两个数组存储
模板：P13825 【模板】线段树 1.5
code:
CPP
#include <bits/stdc++.h>
#define int unsigned long long
#define endl '\n'
using namespace std; 

const int maxn = 1e5 + 10;
struct seg {
    int t[maxn * 120], lz[maxn * 120], ls[maxn * 120], rs[maxn * 120], tot = 1;
    #define ls ls[x]
    #define rs rs[x]
    #define mid ((l + r) >> 1)
    void pushup(int x) { t[x] = t[ls] + t[rs]; }
    void pushdown(int x, int l, int r) {
        if (!lz[x]) return; 
        if (!ls) ls = ++tot;
        if (!rs) rs = ++tot;
        t[ls] += lz[x] * (mid - l + 1);
        t[rs] += lz[x] * (r - mid);
        lz[ls] += lz[x], lz[rs] += lz[x];
        lz[x] = 0;
    }
    void upd(int x, int l, int r, int ml, int mr, int k) {
        if (ml <= l && r <= mr) t[x] += (r - l + 1) * k, lz[x] += k;
        else {
            pushdown(x, l, r);
            if (ml <= mid) {
                if (!ls) ls = ++tot;
                upd(ls, l, mid, ml, mr, k);
            }
            if (mr > mid) {
                if (!rs) rs = ++tot;
                upd(rs, mid + 1, r, ml, mr, k);
            }
            pushup(x);
        }   
    }
    int qry(int x, int l, int r, int ml, int mr) {
        if (!x) return 0;
        if (ml <= l && r <= mr) return t[x];
        else {
            pushdown(x, l, r);
            int ans = 0;
            if (ml <= mid) ans += qry(ls, l, mid, ml, mr);
            if (mr > mid) ans += qry(rs, mid + 1, r, ml, mr);
            return ans;
        }  
    }
} t;
signed main() {
    ios::sync_with_stdio(0); 
    cin.tie(0), cout.tie(0); 
    int n, m;
    cin >> n >> m;
    while (m--) {
        int op, l, r;
        cin >> op >> l >> r;
        if (op == 1) {
            int x;
            cin >> x;
            t.upd(1, 1, n, l, r, x);
        }
        else cout << t.qry(1, 1, n, l, r) + (r - l + 1) * (r + l) / 2 << endl;
    }
    return 0; 
}
（还卡long long坏题）

权值线段树

权值线段树的节点维护的是权值在一段区间内的信息，一般是出现次数之类的信息
形态：
这上面每个节点维护的是权值在 l∼rl\sim r 的数出现过多少次，那么自然，我们就能想到线段树的维护方式，因为它可以合并
所以权值线段树的基本框架相当于是一个单修区查的线段树，单修是每次加入一个数时，修改那个权值对应的出现次数，区查就是查询 l∼rl\sim r 内的数出现了多少次
模板没多少，就拿 P3369 【模板】普通平衡树 当板子吧
code:
CPP

线段树上二分

势能线段树

吉司机线段树

可持久化线段树

李超线段树

线段树合并

线段树分裂

线段树分治

猫树

zkw线段树

优化建图

维护复杂信息

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...