专栏文章

题解：P12480 [集训队互测 2024] Classical Counting Problem

LLehe
P12480题解参与者 5已保存评论 4

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
4 条
当前快照
1 份
快照标识符
@miouzdmw
此快照首次捕获于
2025/12/03 01:35
3 个月前
此快照最后确认于
2025/12/03 01:35
3 个月前
查看原文
比较考验基本功的题，需要一步步慢慢转化。
首先考虑刻画合法连通块具有哪些性质。注意到合法性只跟块内的最小值 mnmn 和最大值 mxmx 有关。由于删除过程不好直接考虑，所以转化为倒着加点。
显然，每次加入的点必须不在 [mn,mx][mn,mx] 范围内。也就是说我们得到了必要条件：与连通块相邻的点必须 <mn\lt mn 或 >mx\gt mx。我们发现这个条件也是充分的。具体地，在满足条件的情况下，与当前的连通块相邻的任何一个点 vv 都能被加入（不妨设 v<mnv \lt mn），这时候值域更新为 [v,mx][v,mx]。同时我们以 vv 为中心往外扩展，把包含 vv 的值域在 [v,mx][v,mx] 的整个连通块都加入，我们发现这样操作后构成的新连通块仍然满足条件，因此可以一直这样扩展下去，直到成为原树。
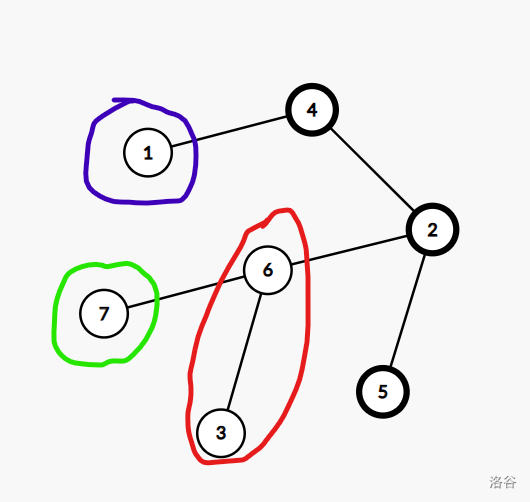
例如上图 4−2−54-2-5 就是一个合法连通块，依次加入 11、3−63-6、77 可以扩展成原树，对应的删除操作就是依次删除 77、66 和 11。
回到原问题。由于我们刚才刻画的条件唯一的限制与 mnmn 和 mxmx 有关，因此我们先考虑固定这两个值计算贡献。显然这两个点 mn↔mxmn \leftrightarrow mx 路径上的所有点必须被包含。如果之间有不在 [mn,mx][mn,mx] 的点则肯定不合法。否则的话考虑我们刚才得出的条件，我们发现可以类似地进行扩展，把所有相邻的值域内的点扩展入连通块，直到形成一个极大连通块为止。也就是说，[mn,mx][mn,mx] 能确定的最后的连通块形态是唯一的。
这时候容易实现 O(n3)O(n^3) 暴力。同时不难想到优化，固定 mnmn 并从小到大枚举 mxmx，用并查集等维护连通块即可做到约 O(n2)O(n^2)。
考虑优化。直接枚举 mnmn 或 mxmx 任何一个都难以直接计算。联想到 mnmn 到 mxmx 的路径必选这一条件，可以想到使用点分治来处理路径信息。
但是答案乘上 sizesize 还是难以维护。联想到经典套路：可以把 sizesize 拆开，多加入一维 vv，三元组 (mn,mx,v)(mn,mx,v) 表示 vv 能够在 mnmn 和 mxmx 确定的连通块内，即求所有三元组 mn×mxmn \times mx 的和。
现在的条件要好刻画多了。发现 vv 只需要满足到 mn↔mxmn \leftrightarrow mx 路径上经过的所有点都在 [mn,mx][mn,mx] 之间，就一定能被扩展到。
回到点分治过程。我们现在确定了一个分治中心 rtrt 作为 mnmn、mxmx 和 vv 的 lca\text{lca}，重新描述一下我们的限制：首先 mn↔mxmn \leftrightarrow mx 路径上的点都要在 [mn,mx][mn,mx] 之间，其次 vv 到这条路径经过的点也要在 [mn,mx][mn,mx] 之间。注意到这两段能被 mn→rtmn \to rt、mx→rtmx \to rt 与 v→rtv \to rt 三段恰好覆盖。所以只需要转而考虑这三段即可。
所有限制现在都跟每个点到 rtrt 路径上的点有关了。更进一步地，对于每个点 uu 计算 lul_u 和 rur_u 表示 u→rtu \to rt 路径上的点的最小值和最大值。我们的限制可以被重新表述为：
{rmn≤mxlmx≥mnmn≤lv≤rv≤mx\begin{cases} r_{mn} \le mx \\ l_{mx} \ge mn \\ mn \le l_v \le r_v \le mx\\ \end{cases}
现在问题简化为：给定若干 (u,lu,ru)(u,l_u,r_u) 三元组，求满足上述不等式的 (mn,mx,v)(mn,mx,v) 的 mn×mxmn \times mx 之和。考虑枚举 mxmx，即按照所有点的 rxr_x 排序后扫描线。
开一颗线段树，维护 mnmn 在每个区间内时的答案 ss。同时每个区间还要维护区间内已经被加入（即 rmn≤mxr_{mn} \le mx）的 mnmn 的和 valval，以及区间内每个 mnmn 对应的恰好满足 lv=mnl_v=mn 的 vv 的数量 cc，作为辅助。
每次加入一个点，有三种情况：
  • uu 作为 vv。这时候 uu 应在扫描线到 rur_u 处被加入。加入时产生贡献为让 ≤lu\le l_u 的 mnmn 答案加上已经被加进来的 mnmn 的和，即对于 [1,lu][1,l_u] 执行 s←s+vals \leftarrow s+val，同时 lul_u 处合法 vv 数量增加，即在 lul_u 处执行 c←c+1c \leftarrow c+1。
  • uu 作为 mnmn。需满足 lu=ul_u=u。这时候 uu 应在扫描线到 rur_u 处被加入。加入时这个点第一次合法，因此对于 uu 点处执行 val←uval \leftarrow u。同时 uu 作为 mnmn 能对答案产生的贡献也要计算，与它能产生的贡献的 vv 有 ∑i=unci\sum\limits_{i=u}^nc_i 个（可以线段树区间查询求出，记作 CC），故在 uu 点处执行 s←C×us \leftarrow C \times u。
  • uu 作为 mxmx。需满足 ru=ur_u=u。这时候 uu 应在扫描线恰好到 uu 处时进行查询。即求 [lu,u][l_u,u] 区间内所有 ss 的和，乘上 uu 并加入答案。
总结一下，我们要用线段树维护三个数组 ss、valval 与 cc，支持单点修改、区间 s←s+vals \leftarrow s+val 与区间求和三种操作。
这样已经基本解决了。注意当 vv 跟 mnmn 和 mxmx 均在同一子树内时贡献会算重，对每棵子树再跑一遍扫描线算出贡献减掉即可。
每层分治总共需要对 O(n)O(n) 个点跑扫描线，每一层的复杂度为 O(nlog⁡n)O(n \log n)。总的时间复杂度为 O(nlog⁡2n)O(n \log^2 n)，可以通过。
代码虽然稍长但并不难写，细节与边界情况也不是很多。
以下是本人实现，代码较丑，人傻常数大，仅供参考。
CPP
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ull unsigned long long
#define pii pair<int,int>
#define fir first
#define sec second
#define chmin(a,b) a=min(a,b)
#define chmax(a,b) a=max(a,b)
#define pb push_back
const int inf=0x3f3f3f3f3f3f3f3f;
constexpr int mod=(1LL<<32)-1;

int ans;

int n,sz[100010],vis[100010],mx[100010],l[100010],r[100010],msz;
vector<int>g[100010];
vector<int>tmp;
void dfs1(int u,int f){sz[u]=1;for(auto v:g[u])if(v!=f&&!vis[v])dfs1(v,u),sz[u]+=sz[v];}
void dfs2(int u,int f,int &rt){mx[u]=msz-sz[u];for(auto v:g[u]){if(v!=f&&!vis[v])dfs2(v,u,rt),chmax(mx[u],sz[v]);}if(mx[u]<=mx[rt])rt=u;}
 
void dfs3(int u,int f)
{
	l[u]=min(l[f],u),r[u]=max(r[f],u),tmp.pb(u);
	for(auto v:g[u])if(!vis[v]&&v!=f)dfs3(v,u);
}

/*
--------------------- 
*/

struct tnode
{
	int l,r,s,v,c,tag;
	tnode(){}
	tnode(int _l,int _r,int _s,int _v,int _c,int _tag)
	{l=_l,r=_r,s=_s,v=_v,c=_c,tag=_tag;}
	//s: 区间内所有 mn 对答案的贡献
	//v: 区间内所有合法的 mn 的和
	//c: 区间内合法 v 的数量 
}t[400010];
#define ls rt<<1
#define rs rt<<1|1
void pushup(int rt)
{
	t[rt].s=(t[ls].s+t[rs].s)&mod;
	t[rt].v=(t[ls].v+t[rs].v)&mod;
	t[rt].c=(t[ls].c+t[rs].c)&mod;
}
void change(int rt,int tag){(t[rt].s+=t[rt].v*tag)&=mod,(t[rt].tag+=tag)&=mod;}
void pushdown(int rt){if(t[rt].tag)change(ls,t[rt].tag),change(rs,t[rt].tag),t[rt].tag=0;}
void build(int rt,int l,int r)
{
	t[rt]={l,r,0,0,0,0};
	if(l==r)return;
	int mid=l+r>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
}
void update(int rt,int x,int v,int op)
{
	if(t[rt].l==t[rt].r)
	{
		if(op==0)(t[rt].s+=v)&=mod;
		else if(op==1)(t[rt].v+=v)&=mod;
		else (t[rt].c+=v)&=mod;
		return;
	}
	pushdown(rt);
	if(x<=t[ls].r)update(ls,x,v,op);
	else update(rs,x,v,op);
	pushup(rt);
}
void add(int rt,int l,int r,int v)
{
	if(l<=t[rt].l&&r>=t[rt].r){change(rt,v);return;}
	pushdown(rt);
	if(l<=t[ls].r)add(ls,l,r,v);
	if(r>=t[rs].l)add(rs,l,r,v);
	pushup(rt);
}
int query(int rt,int l,int r,int op)
{
	if(l<=t[rt].l&&r>=t[rt].r)return op?(op==1?t[rt].v:t[rt].c):t[rt].s;
	pushdown(rt);
	int ans=0;
	if(l<=t[ls].r)ans+=query(ls,l,r,op);
	if(r>=t[rs].l)ans+=query(rs,l,r,op);
	return ans&mod;
}

/*
--------------------- 
*/

int m,b[300010];
vector<int>q[300010];
int calc()
{
	int ans=0;
	m=0;
	for(auto u:tmp)b[++m]=u,b[++m]=l[u],b[++m]=r[u];
	sort(b+1,b+m+1);
	m=unique(b+1,b+m+1)-b-1;
	build(1,1,m);
	for(int i=1;i<=m;i++)q[i].clear();
	for(auto u:tmp)
	{
		int p=lower_bound(b+1,b+m+1,u)-b;
		q[p].pb(u);
		int rp=lower_bound(b+1,b+m+1,r[u])-b;
		q[rp].pb(-u);
	}
	for(int i=1;i<=m;i++)
	{
		sort(q[i].begin(),q[i].end());
		for(auto u:q[i])
		{
			
			if(u<0)
			{
				u=-u;
				int p=lower_bound(b+1,b+m+1,u)-b;
				int lp=lower_bound(b+1,b+m+1,l[u])-b;
				
				//u 为 v 
				add(1,1,lp,1);
				update(1,lp,1,2);
				
				//u 为 mn 
				if(u==l[u])
				{
					int q=query(1,p,p,1);
					update(1,p,u,1);
					int t=query(1,p,m,2);
					update(1,p,(u*t)&mod,0);
				}
			}
			else if(u==r[u])
			{
				//u 为 mx 
				int p=lower_bound(b+1,b+m+1,u)-b;
				int lp=lower_bound(b+1,b+m+1,l[u])-b;
				(ans+=query(1,1,lp,0)*u)&=mod;
			}
		}
	}
	return ans;
}

void dfs(int u)
{
	dfs1(u,0);
	msz=sz[u],mx[0]=inf;
	int rt=0;
	dfs2(u,0,rt);
	
	l[rt]=r[rt]=rt;
	vector<int>tr; 
	tr.pb(rt);
	int pans=0;
	for(auto v:g[rt])if(!vis[v])
	{
		tmp.clear();
		if(!vis[v])dfs3(v,rt);
		int q=calc();
		(pans+=mod+1-q)&=mod;
		for(auto x:tmp)tr.pb(x);
	}
	tmp=tr;
	int q=calc();
	pans+=q;
	(ans+=pans)&=mod;
	
	vis[rt]=1;
	for(auto v:g[rt])if(!vis[v])dfs(v);
}
void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)g[i].clear(),vis[i]=0;
	for(int i=1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		g[u].pb(v);
		g[v].pb(u);
	}
	ans=0;
	dfs(1);
	cout<<ans<<endl;
	return;
}
signed main()
{
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

评论

共 4 条评论，欢迎与作者交流。

正在加载评论...