专栏文章

2025国庆集训的可爱题目

___CrossBow_EXE__
个人记录参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@minqmxzh
此快照首次捕获于
2025/12/02 06:45
3 个月前
此快照最后确认于
2025/12/02 06:45
3 个月前
查看原文

10.1 模拟赛

T1

pro

给出两个二进制数 a,ba,b，问 a mod ba\bmod b 是否为 00。
a≤2105,b≤2200a \le 2^{10^5},b \le 2^{200}

sol

考虑除法竖式，显然除数在一直向右平移。那么对于被除数上一位 11，只能在当前位置解决。否则后面就够不到这一位了。
所以，从左到右遍历被除数，如果当前除数对应的那一块小于除数则无解，否则就减去，继续扫。扫到最后，如果什么都不剩就输出 Yes。

T2

pro

CEXE 在数轴上扫垃圾，每个垃圾在 aia_i。最初 CEXE 在 ss 的位置。CEXE 想清理总共 mm 个垃圾，求最小移动距离。
n≤106n \le 10^6

sol

显然有性质：
  • 扫 >m>m 个不如扫 mm 个
  • 扫间断的不如扫连续的
所以，对于所有垃圾排序，扫描每个连续的长度为 mm 的区间。对每个区间答案取最小即可。

T3

pro

给出 nn 个点对，求满足下列条件的三元组个数：
  • y1=y3y_1=y_3
  • x1<x2<x3x_1<x_2<x_3
  • x3−x1≤y1−y2x_3-x_1 \le y_1-y_2
n≤3×103n \le 3 \times 10^3

sol

B 点什么性质都没有，考虑枚举 AC 点。
当我们知道 AC 点时，我们相当于知道了 B 点的范围。对整个星空做一个前缀和，找出有多少点在范围内即可。

T4

pro

nn 个 lyx 排成一排，每个 lyx 有重量 aia_i。对于两个相邻的 lyx，如果一个 lyx 的重量严格大于另一个，那这个重量大的 lyx 就会吃掉重量小的 lyx。被吃掉的将会消失，它的两边将会相邻。而重量大的 lyx 重量将变为 ai∣aja_i|a_j。求每个 lyx 最后可能的最大重量。

sol

显然，让 aia_i 的某一位发生变化（零变一）的有效操作个数最多只有 log⁡ai\log a_i 个。而除了有效操作的无效操作一定都可以做，而有效操作则不一定。
这样，我们从 ii 想两边拓展，快速找到第一个 ai+k∣ai≠aia_{i+k}|a_i \ne a_i 的 kk。（以向右为例）
这可以用线段树上二分快速查找。但还有简单的办法：ST 表上倍增。对 ST 表的定义稍加修改：sti,jst_{i,j} 表示从 ii 开始的 2j2^j 长度区间能否拓展。这两种方法的复杂度都是 log⁡\log 级别。

10.1 数据结构专题

扫描线

扫描线不是矩阵面积并！

P1908 逆序对

给出序列，求满足 i<ji<j 且 ai>aja_i>a_j 的数对 (i,j)(i,j) 的个数。
把每个数当作坐标系上坐标为 (i,ai)(i,a_i) 的点，则问题就变为一个点左边有多少比他高的点。在纵坐标（值域）上用树状数组维护即可。

P5677 配对统计

给出序列，对于 (x,y)(x,y)，如果对于所有 ii 满足 ∣ax−ay∣≤∣ax−ai∣(i≠x)|a_x-a_y|\le|a_x-a_i|(i \ne x)，则称 (x,y)(x,y) 为一组好的配对。每次询问区间 [l,r][l,r] 中含有多少组好的配对。
显然对于一个 xx，满足条件的 yy 最多只有两个：坐标系上 axa_x 左边和右边两个点。那么，给出 xx，我们能迅速找到满足条件的 yy。可以预处理所有的好配对。
重点在如何统计答案。显然要离线询问，把询问排序后动态插入好配对。维护一个树状数组，对于一个询问 [l,r][l,r]，答案为 ask(r)-ask(l-1)。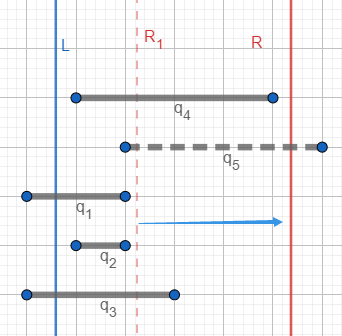
如图，对于每次 rr 向右移动，都把右端点进入 [l,r][l,r] 区间内的好配对加入树状数组，ask(x) 询问左端点在 [1,x][1,x] 范围内的好配对数量。对于每个询问统计答案即可。

P1972 HH的项链

区间数颜色。
对于一个询问 [l,r][l,r] 离线下来，在一个 vector<pii> 数组中，按右端点分类（p[r].push_back(mkp(l,i))），并对每个值记一个 lstailst_{a_i} 表示上一个 aia_i 的位置。维护树状数组，ask(i) 表示 [1∼i][1 \sim i] 的颜色个数。
遍历 aa 序列，记变量 cntcnt 表示 1∼i1 \sim i 有多少颜色。如果 aia_i 已经出现过，就在树状数组上 add(lst[a[i]],-1)，以及 add(i,1)。表示在 [lstai,i][lst_{a_i},i] 之间的询问多了一种颜色。
最后，遍历右端点为 ii 的所有询问，询问 [l,i][l,i] 的答案即为 cnt−ask(l−1)cnt-ask(l-1)。

10.2 模拟赛

T1

pro

Alex866 有一家公司，手下有 nn 个 lyx，每个 lyx 一天可以完成一个任务。后面 mm 天每天有 aia_i 个任务，如果一个 lyx 连续工作两天或以上，就会产生天数少一的疲劳值。求最小劳累值。
1≤n≤1061 \le n \le 10^6

sol

每天对答案的贡献为 max⁡{0,ai−(n−ai−1)}\max\{0,a_i-(n-a_{i-1})\}。
这式子推了一个小时

T2

pro

一个序列，我们要删掉若干元素，把剩余元素排列，使得新的序列包含 1∼m1 \sim m 的排列。无法出现排列输出 -1。
1≤n,m,ai≤1061 \le n,m,a_i \le 10^6

sol

首先有：当我们找到一个区间包含 1∼m1\sim m 的排列后，区间两边的序列都不用考虑。mm 是定值，为了删去的数最少，找到的区间长度需要最短。
那么，问题就变为找到一个最短区间，包含 1∼m1\sim m 的排列。二分答案或双指针即可。
找到区间后，把区间内多余的数统计进答案即可。
记得判 -1，否则挂 10pts（悲

T3

pro

两个字符串 S,TS,T，其中 SS 由小写字母组成，TT 由小写字母和问号组成。打乱 SS 后，原本第 ii 个位置上的字符到了 pip_i。一定有 ∣i−pi∣≤k|i-p_i| \le k。问有多少 pp 满足条件，答案对 998244353998244353 取模。

sol

注意到 0≤k≤30 \le k \le 3，想到状压 dp。
对于 SS 一个字符，它只能填到 i−k∼i+ki-k \sim i+k 的位置，只有 77 个。所以定义状态 dpi,sdp_{i,s} 表示 S[1…i]S[1 \dots i] 已经填上，且 i−k∼i+ki-k \sim i+k 状态为 ss 的方案数。ss 中 11 表示 ii 能填到这里，00 表示不能填。
转移如下：首先 ss 首位必须是 00，否则后面无法填到 i−ki-k 位置；接着考虑从 [i−k,i+k][i-k,i+k] 转移到 [i−k+1,i+k+1][i-k+1,i+k+1]，如果新的一位是 ? 则末位为 11，如果新的一个字符和 ii 的字符一样也为 11，否则为 00。采用刷表法。答案即 dpn,0dp_{n,0}。时间复杂度 O(nk22k+1)O(nk2^{2k+1})。

T4

pro

一棵树根为 11，给出 mm 个询问，每次砍断 kk 条边（不是真的砍断），求砍断后的所有联通点对的距离和。

sol

放个老师题解。
题解源代码

椴树

算法零

按题意模拟, 每次从一个点出发遍历整个连通块, 计算到达每个点的距离, 求和. 单次询问 O(n2)O(n^2), 总复杂度 O(n2m)O(n^2m), 期望 15′15'.

算法一

每一场梦进行一次树上 DP, 统计所有联通块的答案, 最后求和.
考虑每条边的贡献而不是路径的贡献. 对于一条边, 两侧的点数假如是 aa, bb, 那么这条边就会被 abab 条路径统计.
所以只需要统计连通块上每个子树的大小, 连通块的大小即可.
CPP
struct Node {
  vector<Node*> Sons;
  Node* Fa, * Rot;//父亲, 连通块的根
  bool Rt;//是否是连通块的根
  unsigned Size;
  void DFS() {//计算连通块内的 Size
    Size = 1;
    if (Rt) Rot = this;
    for (Node* i : Sons) if (i != Fa) {
      i->Fa = this;
      if (!(i->Rt))  i->Rot = Rot;
      else i->Rot = i;
      i->DFS();
      if (!(i->Rt)) Size += i->Size;
    }
  }
}N[200005];
每次回答询问:
CPP
for (unsigned j(0); j < A; ++j) N[Ban[j]].Rt = 1; //设置连通块的根
N[1].Rt = 1, N[1].DFS();
for (unsigned j(1); j <= n; ++j) if (!N[j].Rt) //非根点和父亲相连的边
  Ans += (unsigned long long)N[j].Size * (N[j].Rot->Size - N[j].Size);
for (unsigned j(0); j < A; ++j) N[Ban[j]].Rt = 0; //撤回设置
printf("%llu\n", Ans);
复杂度 O(nm)O(nm), 期望得分 30′30'.

算法二

算法一求的是:
∑i=1nSizei∗(SizeRoti−Sizei)\sum_{i = 1}^n Size_i * (Size_{Rot_i} - Size_i)
记对整棵树来说, 子树大小为 TotiTot_i, 一个点 ii 下方 (不含 ii) 可以直达的根构成集合 SubiSub_i. (直达即为存在简单路径连接两点, 且不经过其他根) 那么应当有:
Sizei=Toti−∑j∈SubiTotjSize_i = Tot_i - \sum_{j \in Sub_i} Tot_j
为了让每次询问的复杂度低于 O(n)O(n), 我们应该把计算集中到连通块的根上. 这样就可以在只访问 kk 个点的情况下, 回答一次询问. 为了能够快速定位每个根节点的直达根节点, 我们遍历根的方法, 是将所有根按 DFS 序从小到大枚举. 这相当于 DFS 整棵树, 但是跳过非根节点. 这样遍历所有根的时候, 用一个栈就可以维护当前点上方所有的根节点, 栈顶也就是上方的直达根节点 VirFa.
下面是遍历过程 (不含计算):
CPP
k = RD();
vector<pair<unsigned, unsigned>> Lst;
for (unsigned j(1); j <= k; ++j) {
  B = RD();
  if (B == 1) continue;
  Lst.push_back({ N[B].DFN, B });
}
Lst.push_back({ 1, 1 });//1号点也是一个根
sort(Lst.begin(), Lst.end());//按 DFN 排序所有根
stack<Node*> Stk; //栈, 从栈底到栈顶是当前节点上方, 深度从浅到深的根节点
for (auto j : Lst) {
  Node* Cur(N + j.second);
  while (Stk.size() && (!(Stk.top()->InTree(j.first)))) Stk.pop();
  Cur->VirFa = Stk.size() ? Stk.top() : NULL;//上方直达根节点
  Stk.push(N + j.second);
}
由于存在排序, 所以遍历的复杂度是 O(klog⁡k)O(k \log k) 的.
由于无法每次重新计算每个点的 SizeSize, 而每个点的 TotTot 是常数, 可以直接利用. 也就是说, 我们要避免显式地计算出 SizeiSize_i, 而是带入 TotTot, 答案可以表达为:
∑i=1nSizei∗(SizeRoti−Sizei)=∑i=1n(Toti−∑j∈SubiTotj)(SizeRoti−Toti+∑j∈SubiTotj)=∑i=1nTotiSizeRoti−SizeRoti∑j∈SubiTotj−Toti2+2Toti∑j∈SubiTotj−(∑j∈SubiTotj)2\sum_{i = 1}^n Size_i * (Size_{Rot_i} - Size_i)\\ = \sum_{i = 1}^n (Tot_i - \sum_{j \in Sub_i} Tot_j)(Size_{Rot_i} - Tot_i + \sum_{j \in Sub_i} Tot_j)\\ = \sum_{i = 1}^n Tot_iSize_{Rot_i} - Size_{Rot_i}\sum_{j \in Sub_i} Tot_j - Tot_i^2 + 2Tot_i\sum_{j \in Sub_i} Tot_j - (\sum_{j \in Sub_i} Tot_j)^2\\
发现答案的表达共有五项, 第三项 −Toti2-Tot_i^2 是常数, O(n)O(n) 预处理即可. 剩下的项分别计算.
第一项 TotiSizeRotiTot_iSize_{Rot_i}. 考虑对一个连通块统一计算, 即为连通块 TotTot 总和乘以根的 SizeSize. 其中连通块 TotTot 总和可以预处理整棵树意义上 (不断边) 的 TotTot 子树和 SumTot, 用 RotRot 的 SumTot 减去所有 SubRotSub_{Rot} 中元素的 SumTot 即为连通块 TotTot 总和. 而根的 SizeSize 也是相似的计算方式, 即 RotRot 的 SizeSize 减去所有 SubRotSub_{Rot} 中元素的 SizeSize. 预处理 O(n)O(n), 单次询问复杂度 O(k)O(k).
第二项 −SizeRoti∑j∈SubiTotj- Size_{Rot_i}\sum_{j \in Sub_i} Tot_j 考虑计算每个根 jj 对于它的 VirFa 的贡献. 发现 SizeVirFajTotjSize_{VirFa_j}Tot_j 一共会被统计 Depj−DepVirFajDep_j - Dep_{VirFa_j} 次. 这是因为符合条件的全部 ii 即为 jj 到 VirFa 的上闭下开路径上的所有点, 而这些点的数量即为 Depj−DepVirFajDep_j - Dep_{VirFa_j}. 预处理 O(n)O(n), 单次询问 O(k)O(k).
我们先看第五项, −(∑j∈SubiTotj)2- (\sum_{j \in Sub_i} Tot_j)^2, 考虑 jj 对每个 ii 的贡献. 和第二项相似, jj 会向 jj 到 VirFa 上闭下开路径上所有 ii 的 ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 产生 TotjTot_j 的贡献. 维护这些贡献需要一个数据结构, 支持路径加法, 全局求平方和. 用线段树配合树链剖分可以处理, 预处理 O(n)O(n), 单次询问 O(klog⁡2n)O(k \log^2 n).
第四项 2Toti∑j∈SubiTotj2Tot_i\sum_{j \in Sub_i} Tot_j, 仍然是计算根 jj 的贡献, 仍然是对 ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 贡献, 需要询问的值是全局加权和. 每个点的权值 2Toti2Tot_i 是常数, 同样可以用树链剖分维护, 预处理 O(n)O(n), 单次询问 O(klog⁡2n)O(k \log^2 n).
四五项所需要的线段树需要维护: 区间 ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 和 Sum, 区间 ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 平方和 SumSq, ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 加权和 Mul (权值为 2Toti2 Tot_i), LazyTag Tag (未下传的, ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j 累加的值).
由于权值 TotiTot_i 是常数, 所以预处理前缀和 PreSum 备用, 可以快速求区间和, 用于维护 Mul.
CPP
unsigned long long PreSum[200005];
struct Seg {
  Seg* LS, * RS;
  unsigned L, R;
  unsigned long long Sum, SumSq, Mul, Tag;
  void Udt(unsigned long long x) {
    Mul += (PreSum[R] - PreSum[L - 1]) * x;
    SumSq += Sum * x * 2;
    SumSq += x * x * (R - L + 1);
    Sum += (R - L + 1) * x;
    Tag += x;
  }
  inline void PsDw() {
    if (!Tag) return;
    LS->Udt(Tag), RS->Udt(Tag), Tag = 0;
  }
  inline void PsUp() {
    Mul = LS->Mul + RS->Mul;
    Sum = LS->Sum + RS->Sum;
    SumSq = LS->SumSq + RS->SumSq;
  }
  void Add() {
    if (QL <= L && R <= QR) {
      Udt(Val); return;
    }
    unsigned Mid((L + R) >> 1);
    PsDw();
    if (QL <= LS->R) LS->Add();
    if (QR > Mid) RS->Add();
    PsUp();
  }
}S[400005], * CntS(S);
树链剖分的实现上, 有几个细节: 一个是由于需要多次询问, 但是不能每次清空线段树, 所以需要记录每一次区间加, 在询问结束后减去这些操作, 将线段树维护的值复原:
CPP
vector<pair<pair<unsigned, unsigned>, unsigned long long>> Added;
void Rewind() {
  for (auto i : Added) {
    Val = -i.second, QL = i.first.first, QR = i.first.second;
    S[1].Add();
  }
  Added.clear();
}
另一个是我们操作的所有路径都是祖先和后代的路径 (不拐弯), 所以只需要跳一个节点即可, 无需两个节点交替跳:
CPP
void Add(Node* x, Node* y) {
  while (y->Top != x->Top) {
    QL = y->Top->DFN, QR = y->DFN;
    Added.push_back({ { QL, QR }, Val });
    S[1].Add();
    y = y->Top->Fa;
  }
  QL = x->DFN, QR= y->DFN;
  Added.push_back({ { QL, QR }, Val });
  S[1].Add();
}
这样我们就可以通过 O(k)O(k) 次操作, 以 O(k(log⁡2n+log⁡k))O(k (\log^2 n + \log k)) 的复杂度完成一次询问. 总复杂度 O(n+∑klog⁡2n)O(n + \sum k \log^2 n).
计算过程中可能会出现数字超过 unsigned long long 的范围的情况, 但是可以证明答案一定不会超过 n3n^3, 在 unsigned long long 范围内. 所以即使中间过程爆 unsigned long long, 自然溢出取模可以保证最后结果是正确的.
这个算法在常数好的情况下, 已经可以通过本题了.

算法三

仍然审视在计算中很关键的值 ∑j∈SubiTotj\sum_{j \in Sub_i} Tot_j, 记为 SubTotiSubTot_i. 我们发现, 不同的 SubiSub_i 集合的数量就是对 kk 个点建虚树的点数, 也就是不超过 2k2k. 我们将 SubSub 集合相同的点集称为 SubSub 等价类.
这里建虚树的关键点其实是每个根的父亲, 因为每个根对从父亲开始到上方直达根路径上的 SubSub 集合产生贡献. 对于 SubSub 集合相同的路径, 路径最下方的实点对应虚树上的一个虚点, 路径最上方点的父亲也对应一个虚点, 这两个虚点在虚树上是父子关系. (为了处理边界情况, 我们给原来的 11 号点加一个父亲 00 号点, 00 号点不是本题意义中的连通块根, 也不属于任何连通块)
CPP
struct VirTree {
  vector<VirTree*> Sons;
  VirTree* Fa;
  Node* Real, * Rot;//分别表示: 虚点对应的实点, 实点所在的连通块根
  unsigned long long SubTot;// Real 下方直达根的 Tot 总和
}V[200005], * CntV(V);
unordered_map<Node*, VirTree*> VirMap;//实点到虚点的映射
vector<pair<unsigned, VirTree*>> VirLst;//按实点的 DFN 排列虚点
void Udt(Node* x, unsigned long long y, Node* Rot) {// x 是根, 对父亲对应的虚点产生贡献
  if (VirMap.find(x) == VirMap.end()) {
    VirMap[x] = ++CntV;
    CntV->Real = x, CntV->Sons.clear(), CntV->Fa = NULL;
    CntV->SubTot = y, CntV->Rot = Rot;
    VirLst.push_back({ x->DFN, CntV });
    return;
  }
  VirMap[x]->SubTot += y;
}
void NewDot(Node* x, Node* Rot) {//x 不存在根作为儿子, 但是是两个虚点的 LCA
  VirMap[x] = ++CntV;
  CntV->Real = x, CntV->Sons.clear(), CntV->Fa = NULL;
  CntV->SubTot = 0, CntV->Rot = Rot;
}
前三项和算法二相同, 不再赘述. 建出虚树后, 用一次 DFS 同时计算第四项和第五项:
CPP
void VirTree::DFS() {//DFS 之前, SubTot 的值为对应实点的满足是根的儿子的 Tot 总和
  for (auto i : Sons) {
    i->DFS();
    if (i->Rot == Rot) SubTot += i->SubTot;//Rot 不同, 下方的根不直达, 不能传递
  }
  if (Fa) {
    Ans += SubTot * 2 * (Real->TotDep - Fa->Real->TotDep); //第四项
    Ans -= SubTot * SubTot * (Real->Dep - Fa->Real->Dep); //第五项
  }
}
提前处理的 TotDep 是从 00 号点累加到 ii 点的 TotTot, 这里的作用是用树上前缀和快速求区间 TotTot 和. 在 DFS 的过程中, 计算每个点的 SubTot, 然后一次性计算整个 SubSub 等价类的所有贡献.
单次询问复杂度 O(klog⁡k+log⁡n)O(k \log k + \log n). 也就是 O(klog⁡n)O(k \log n), 总复杂度 O(n+∑klog⁡n)O(n + \sum k \log n).
本题细节较多, 下面放出主函数:
CPP
signed main() {
  n = RD(), m = RD();
  for (unsigned i(1); i < n; ++i) {
    A = RD(), B = RD();
    N[A].Sons.push_back(N + B);
    N[B].Sons.push_back(N + A);
  }
  N->Sons.push_back(N + 1);
  N->Fa = NULL, N->Dep = 0, N->DFS1();
  N->Top = N, N->DFS2();
  for (unsigned i(1); i <= m; ++i) {
    Ans = -N[1].SumSqTot;
    A = RD();
    vector<pair<unsigned, unsigned>> Lst;
    for (unsigned j(1); j <= A; ++j) {
      B = RD();
      if (B == 1) continue;
      N[B].IsRot = 1;
      Lst.push_back({ N[B].DFN, B });
    }
    sort(Lst.begin(), Lst.end());
    stack<Node*> Stk;
    N[1].IsRot = 1, Stk.push(N + 1);
    N[1].Size = N[1].Tot, N[1].BlcTot = N[1].SumTot, N[1].VirTot = 0;
    N[1].VirFa = NULL;
    /*第一项*/
    for (auto j : Lst) {
      Node* Cur(N + j.second);
      Cur->Size = Cur->Tot;
      Cur->BlcTot = Cur->SumTot;
      Cur->VirTot = 0;
      while (Stk.size() && (!(Stk.top()->InTree(j.first)))) {
        Node* Out = Stk.top();
        Ans += Out->BlcTot * Out->Size;
        Stk.pop();
      }
      Cur->VirFa = Stk.size() ? Stk.top() : NULL;
      Stk.push(Cur);
      Cur->VirFa->VirTot += Cur->Tot;
      Cur->VirFa->BlcTot -= Cur->SumTot;
      Cur->VirFa->Size -= Cur->Tot;
    }
    while (Stk.size()) {
      Node* Out = Stk.top();
      Ans += Out->BlcTot * Out->Size;
      Stk.pop();
    }
    /*第二项*/
    for (auto j : Lst) {
      Node* Cur(N + j.second);
      Ans -= Cur->VirFa->Size * Cur->Tot * (Cur->Dep - Cur->VirFa->Dep);
    }
    /*第四五项*/
    VirMap.clear(), VirLst.clear(), CntV = V;
    for (auto j : Lst) Udt(N[j.second].Fa, N[j.second].Tot, N[j.second].VirFa);
    Udt(N, N[1].Tot, N);
    sort(VirLst.begin(), VirLst.end());
    stack <VirTree*> VirStk;
    VirStk.push(VirMap[N]);
    VirTree* Out;
    for (auto j : VirLst) {
      if (j.first == 1) continue;
      Node* Cur((j.second)->Real), * Lca(LCA(Cur, VirStk.top()->Real));
      Out = NULL;
      while (VirStk.size() && (VirStk.top()->Real->Dep > Lca->Dep)) {
        if (Out) Link(VirStk.top(), Out);
        Out = VirStk.top();
        VirStk.pop();
      }
      if (VirStk.top()->Real != Lca) NewDot(Lca, VirMap[Cur]->Rot), VirStk.push(VirMap[Lca]);
      if (Out) Link(VirStk.top(), Out);
      VirStk.push(VirMap[Cur]);
    }
    Out = NULL;
    while (VirStk.size()) {
      if (Out) Link(VirStk.top(), Out);
      Out = VirStk.top();
      VirStk.pop();
    }
    VirMap[N]->DFS();
    N[1].IsRot = 0;
    for (auto j : Lst) N[j.second].IsRot = 0;
    printf("%llu\n", Ans);
  }
  return Wild_Donkey;
}
后记: 由于算法三的 log⁡n\log n 出自 LCA, log⁡k\log k 出自排序, 所以理论上, 结合 O(n)−O(1)O(n)-O(1) RMQ, 还有基数排序, 复杂度可以做到线性, 但是由于树链剖分和 sort 的高效率, 大概率线性是反向优化, 所以实用意义不高.

10.2 大炮专题

P4310

给出序列，求满足如下条件的最长子序列长度：
  • 子序列 bb 满足 bi&bi−1≠0b_i \& b_{i-1} \ne 0
n≤105n \le 10^5
朴素 dp 转移显然是 dpi=max⁡ai&aj≠0dpj+1dp_i=\max_{a_i \& a_j \ne 0} dp_j+1。复杂度 O(n2)O(n^2)。
注意到在二进制下，ii 可以从一个 jj 转移过来当且仅当 aia_i 和 aja_j 有至少一位同时为 11。那么，开一个桶 tkt_k 记录 a1a_1 到 ai−1a_{i-1} 中哪些第 kk 为是 11，在一个 vector 中记录下标。对于新的 ii，枚举 aia_i 是 11 的二进制位，再从桶上对应的区域转移即可。复杂度 O(nlog⁡n)O(n \log n)。
妙啊！

P1941

太长了，看原。
先考虑没有管道的情况。横坐标每次增加 11，可以从列考虑。
额啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊等会补 打个标记

补这里！！！

dpc_e

01 背包。
1≤n≤100,1≤W,wi≤109,1≤vi≤1031 \le n \le 100,1 \le W,w_i \le 10^9,1 \le v_i \le 10^3
发现 WW 好大一坨，不能放到维度，只能把它放到值，而把价值放到维度里。
什么时候才能交换值域定义域呢？
  • 最优性 dp（哪名神人在计数 dp 的时候交换？）
  • 单调性。
定义 dpi,jdp_{i,j} 表示前 ii 个物品，价值达到 jj 的最小体积。显然随着价值增大，体积一定是不降的。这就满足了单调性。
转移很简单：
dpi,j=min⁡(dpi−1,j,dpi−1,j−vi+wi)dp_{i,j}=\min(dp_{i-1,j},dp_{i-1,j-v_i}+w_i)
想得到答案可以枚举价值 jj，找到最小的 dpn,j≤mdp_{n,j}\le m 即可。

P9197

给出序列，将其排列后成为序列 ff，需要满足 ∣f1−f2∣+∣f2−f3∣+⋯+∣fN−1−fN∣≤L| f_1 - f_2| + | f_2 - f_3| + \cdots + | f_{N-1} - f_N| \leq L，求方案数对 109+710^9+7 取模的值。
照着课件写的，不完整
这是连续段 dp。考虑从小到大填入每个数，我们只需要考虑与它连续两个数的大小关系，也就是说只需要考虑已经被填完的连续段的左右端点。
而我们只关心大小，所以每个连续段都是等价的，后来的数一定比连续段内所有数大。
不会……

P5654

pro

P5664 [CSP-S2019] Emiya 家今天的饭

题目描述

Emiya 是个擅长做菜的高中生，他共掌握 nn 种烹饪方法，且会使用 mm 种主要食材做菜。为了方便叙述，我们对烹饪方法从 1∼n1 \sim n 编号，对主要食材从 1∼m1 \sim m 编号。
Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地，Emiya 会做 ai,ja_{i,j} 道不同的使用烹饪方法 ii 和主要食材 jj 的菜（1≤i≤n1 \leq i \leq n、1≤j≤m1 \leq j \leq m），这也意味着 Emiya 总共会做 ∑i=1n∑j=1mai,j\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} a_{i,j} 道不同的菜。
Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友，然而三个人对菜的搭配有不同的要求，更具体地，对于一种包含 kk 道菜的搭配方案而言：
  • Emiya 不会让大家饿肚子，所以将做至少一道菜，即 k≥1k \geq 1
  • Rin 希望品尝不同烹饪方法做出的菜，因此她要求每道菜的烹饪方法互不相同
  • Yazid 不希望品尝太多同一食材做出的菜，因此他要求每种主要食材至多在一半的菜（即 ⌊k2⌋\lfloor \frac{k}{2} \rfloor 道菜）中被使用
这里的 ⌊x⌋\lfloor x \rfloor 为下取整函数，表示不超过 xx 的最大整数。
这些要求难不倒 Emiya，但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同，当且仅当存在至少一道菜在一种方案中出现，而不在另一种方案中出现。
Emiya 找到了你，请你帮他计算，你只需要告诉他符合所有要求的搭配方案数对质数 998,244,353998,244,353 取模的结果。
把两个 sigma 看作行和列，那问题就变成了二维平面选点。
首先考虑列的限制，显然最多一列不合法，可以容斥：用总方案减去不合法方案数。
想要求出总方案数，定义 gi,jg_{i,j} 表示 1∼i1 \sim i 行选了 jj 个点的方案数。转移略。
再看第 cc 列不合法的方案数。令 fi,j,kf_{i,j,k} 表示前 ii 行第 cc 列选了 jj 个，其他列选了 kk 个的方案数。转移略。复杂度 O(n3m)O(n^3m)
考虑优化。注意到统计方案时只关心 j−k>0j-k>0 的 ff 值，可以把 [j][k][j][k] 压缩为 [j−k][j-k]，在 j,kj,k 变化时 +1/−1+1/{-1} 即可。复杂度 O(n2m)O(n^2m)。

10.3 模拟赛

T1

pro

两个等腰三角形，给出它们的三边长，问一个三角形能不能包含另一个。（两个三角形底边必须平行）

sol

简单题，场切了。
根据三边长能算出高（勾股定理），为了防止卡精度可以用平方比较。如果底长的一个更高，那显然可以包含，否则不行。
记得开 long long。

T2

pro

给出由小括号组成的字符串 SS，求把 SS 变成括号串最少要改变多少字符。
n≤106n \le 10^6

sol

看似需要二分（有单调性），实则可以直接计算。
从左到右扫一遍，如果到一个右括号位置时，前缀左括号个数小于右括号个数，则这个位置必须改成左括号。
处理完所有非法右括号后，再找到多余的左括号。这些多余的左括号一定能两两配对，把多余的左括号个数砍一半加上非法右括号的答案即可。

T3

pro

一个无向图，每条边有一个括号边权。给出 mm 组询问，每次给出 u,vu,v，求从 uu 到 vv 的路径中，边权连接后为括号串的最短路径。无法到达输出 −1-1。

sol

最短路问题。
考虑以每个节点为起点跑 dij。用 disx,ydis_{x,y} 表示从起点到 xx，未匹配的左括号数量为 yy 的最短括号串长度。考虑转移，disx,ydis_{x,y} 可以转移到 disp,y±1dis_{p,y \pm 1}。在跑 dij 时转移即可。
注意在跑的时候 y≥0y \ge 0，否则就会出现 )( 这种情况。
判无解显然是对于所有 ii 都有 disv,i=inf⁡dis_{v,i}=\inf。

T4

pro

一个 n×nn \times n 方格，有 mm 次操作，每次操作给出一个子矩形，在子矩形每个位置放上一个颜色为 cc 的物品。求全部操作后，有多少格子包含所有颜色的物品。
1≤n,m≤105,1≤c≤51 \le n,m \le 10^5,1 \le c \le 5

sol

扫描线。当 c=1c=1 时，问题就相当于矩形面积并。
解决 c>1c>1 的方法有两种：
  • 线段树加状压（注意到 c≤5c \le 5）
  • 线段树加容斥
先说第一种。在扫描线的线段树的节点上存一个状压过的集合 xx。当一个节点被操作时，这个节点的 xx 就可以与操作的集合按位或。
具体地，一个节点如果想从左右两个子节点转移，可以枚举左右儿子染色集合 ii。假设每个线段树节点都有一个 cnt[S]cnt[S] 表示当前节点染色情况为 SS 的节点个数，那么 pushup 的式子就为
t.cnti∣S=l.cnti+r.cntit.cnt_{i|S}=l.cnt_i+r.cnt_i
其中 SS 为当前节点的懒标记，| 为按位或。
线段树加容斥比较简单，就是两个颜色加起来再减去重合的。但是五阶容斥的式子又臭又长，不想推了（逃

10.3 树上问题

CF2065F

给定一个 nn 个节点的树，每个节点权值为 aia_i。
定义一个序列的绝对众数为出现次数过半的数。对于所有 1≤x≤n1 \le x \le n，判断有没有一条路径，满足这个路径的绝对众数为 xx。
1≤n≤5×1051 \le n \le 5\times 10^5
结论题。先说一个小结论：只需要考虑长度不超过 33 的路径即可。证明简单，反证法，如果一个 xx 不是长度为 33 的路径的连续众数，那么在一个包含这个小路径的长路径中最多只有 len3\frac{len}{3} 个 xx，远小于 n2+1\frac{n}{2}+1。
知道了结论，分类讨论长度为 22 或 33 即可。如果是 22，那两个节点一定存在父子关系；否则，可以枚举路径的中间点，判断这个中间点的临界点有没有和它权值一样的点。

CF2006A

一棵树，部分节点有权值（0/10/1）。对于每个叶子节点，它的价值计算方法如下：
  • 把根节点到这个节点的路径列出
  • 把权值按深度从小到大排成一排
  • 用序列中 01 的个数减去 10 的个数，结果就是价值
Alex866 和 lyx 在树上玩游戏，它们轮流将一个不确定权值的节点的权值设为 00 或 11。先手的 Alex866 希望最大化总分数，lyx 希望最小化总分数。两个人都因为 CEXE 的指导而绝顶聪明，求最终总分数。
首先有性质：一个叶子节点价值非 00，当且仅当叶子的权值与根不同。
如果根节点权值确定了，先操作叶子节点，就能将答案拉高或降低 11。
否则，先手就设定根节点权值为叶子节点出现次数少的那个权值，转化为上一种情况。
最后，如果叶子节点两种权值的数量相同，两人都要避免操作根（否则就相当于白白浪费一个回合），而是优先操作非根非叶子节点。
放个课件

CF1975D

题面太长了，看图
依旧是结论：最优方案是 A 和 B 先走到一起，然后一起走。证明比较显然，Alex866 都秒了。
所以，一开始 A 和 B 应该走到它们路径的中点。接着，以会合点 xx 为根跑 dp。
定义 fuf_u 表示把 uu 的子树全部染色后回到 uu 的最短时间，gug_u 表示子树全部染色后不必回到 uu 的最短时间。答案为 gxg_x。转移过于简单。
原课件

CF2062D

CF2018C

一个有根树，可以进行若干次操作：删掉一个叶子节点以及与之相连的边。我们最少需要进行多少次操作，才能使所有叶子节点的深度相同？
n≤5×105n \le 5\times 10^5
枚举最终的深度，对于每个深度，都删掉比他深的叶子，再把比他浅的子树连根拔起。比它深的节点用后缀和计算，如何计算比它浅的节点呢？记录一个子树中深度最大值，对深度开一个桶记个数，对这个最大值数组算前缀和即可。
看图：

CF516D

给出一棵树，边有边权。每个点的权值为树上离该点最远的点的距离，询问 qq 次，每次给出 LL，求最大连通块，使得连通块中权值的极差小于等于 LL。
n≤105,q≤50n\le 10^5,q \le 50
考虑以权值最小的节点为根。这样，权值随着深度的增大而增大。
在 dfs 时，如果一个点的儿子们的权值 fv≤fu+Lf_v \le f_u+L，那么 vv 就可以加入连通块。显然连通块一定不会中断。
这样是 O(n2)O(n^2) 的。对于每个 vv，我们预处理出离它最近的祖先 pp，满足 fv>fp+Lf_v>f_p+L。这可以用倍增实现。对于每个节点维护一个桶，跳到一个祖先后就把桶上对应位置的值增加。我们自底向上枚举节点，对于一个节点合并子节点的连通块，直接减去桶上的值即可。

CF734E

给出一棵树，每个点要么是黑色要么是白色。一次操作可以改变一个相同颜色的连通块，求使整棵树颜色相同的最小操作数。
n≤2×105n \le 2\times 10^5
先将同颜色连通块缩点，这样整棵树就是黑白相间的；对这棵树求直径，答案即为直径长度除以二向下取整。

QOJ14304

给出一棵树，点有点权。我们可以删除若干边，删除后会形成若干连通块，连通块的价值为点权极差，总价值为所有连通块价值和。求最大总价值。
n≤106n \le 10^6

10.4 模拟赛

T1

pro

给出三角形两条边，求第三条边的取值个数。

sol

简单题，找较短一边的长度，乘二减一就是答案。

T2

pro

有一些不同颜色的星星（三种颜色），每个星星有一个坐标，找出一个面积最小的矩形，使得这个矩形范围内包含三种颜色的星星各至少一个。

sol

也是简单题，把星星按颜色分类，每次枚举每种颜色的一个星星，根据枚举的三个星星求矩形面积输出即可。

T3

pro

一个由 11 和 −1-1 组成的序列，给出 mm 次操作，一次操作是修改或查询。
  • 修改：给出区间，把区间内的所有 11 变成 −1-1，−1-1 变成 11。
  • 查询：每次查询都定义三个变量 x,y,zx,y,z，x,yx,y 给出，zz 初始为 00。遍历序列，根据值分类：
    • 值为 11：如果 y≠0y \ne 0 则 y--，否则 x++,z++；
    • 值为 −1-1：如果 x≠0x \ne 0 则 x--，否则 y++,z++。
对于每次询问，输出最终的 zz。

sol

先考虑 1 -1 和 -1 1 的情况，会发现这两个序列的结果相同。也就是说，交换两个序列元素结果不会变。那么我们根据冒泡排序的思想，可以得出重要结论：序列的结果与元素顺序无关！\color{white}{\text{序列的结果与元素顺序无关！}}
那么，我们不妨将所有 11 往前放、−1-1 往后放，这样一定是 yy 先减，xx 再减。而 zz 就根据它们减完后的结果算贡献即可。
但是还有区间修。我们注意到结果只与 11 和 −1-1 的数量有关，所以开线段树维护区间 11 和 −1-1 的数量即可。
Alex866orz

T4

pro

NOI2024 D1T1 严格加强版
就是把题面中的判断改成了计数

sol

不会

10.4 基础算法（贪心，二分，倍增）

P11453

数轴上有 nn 个点，给出 kk 个限制：区间 [li,ri][l_i,r_i] 中至少剩余 tit_i 个点。求最多能删除多少点。
简单题。正难则反，求最少能保留多少点。显然保留靠后的点。问题转化为：快速求出最靠后的一个。大根堆维护即可。

P2949

P2949 [USACO09OPEN] Work Scheduling G
按时间排序任务，从小到大枚举任务，如果可以做这个任务就马上做。如果无法做，就在前面找到一个价值最低的任务并把它抛弃。当然前提是最新任务比那个价值最低的价值高。

P11457

P11457 [USACO24DEC] Job Completion G

QOJ14303

Gym105158C

如果序列中出现了 a?????a，那么这个字段必须变成相同的数字。
如果序列中出现 a???b???a???b，那么这个字段也必须相同。
所以我们把序列划分成若干个字段，每个字段内部的数字相同。

10.5 模拟赛

最难的一场比赛

T1

pro

sol

时间具有单调性：晚走一定不会比早走到得早。所以可以二分。
但还不够优，我们从后往前走红绿灯，只要能走就往前走，否则就等灯。显然走到起点的时刻就是最优的。

T2

pro

m≤20,k≤106m \le 20,k \le 10^6

sol

众所周知，求方案数要么是数学要么是计数 dp。这题是计数 dp。
注意到 mm 很小，考虑把一行状压起来。这样复杂度是 O(3mk)O(3^mk)。
定义 dpi,jdp_{i,j} 为一共放了 ii 个黑点，上一行放了 jj 个的方案数，有转移方程
dpi,j=∑j+k≤mdpi−j,kCm−kjdp_{i,j}=\sum_{j+k\le m} dp_{i-j,k}C^{j}_{m-k}
此外，计算 dpi,1∼mdp_{i,1\sim m} 只会用到 dpi−1,1∼m,dpi−2,1∼m,…,dpi−m,1∼mdp_{i-1,1\sim m},dp_{i-2,1 \sim m},\dots,dp_{i-m,1 \sim m}，考虑矩阵快速幂优化 dp。复杂度 O(m3log⁡k)O(m^3\log k)。
这题就是蓝了

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...