专栏文章

题解：P3369 【模板】普通平衡树

IIGA_Indigo
P3369题解参与者 3已保存评论 2

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
2 条
当前快照
1 份
快照标识符
@mipo45r9
此快照首次捕获于
2025/12/03 15:10
3 个月前
此快照最后确认于
2025/12/03 15:10
3 个月前
查看原文
（内容很长，请大家耐心观看，如果是有基础的选手，可以从具体操作开始看。）
（本文有图有详解，有朴素易懂不加修饰的裸板子代码，适合新手食用）

题目大意

要求研究出一个在线的数据结构 MM，要求可以在 MM 中维护下列操作。
  • 插入一个数 xx。
  • 删除一个数 xx（有多个的话仅删除一个）。
  • 查询一个数 xx 的排名（比 xx 小的数的个数 +1+1）。
  • 查询将 MM 中排名为 xx 的数。
  • 查询比 xx 小的最大的数（前驱）。
  • 查询比 xx 大的最小的数（后继）。
暴力不行，我们的数据范围要求在 1≤n≤1051\le n \le 10^5 下解决问题。

大体思路

数据结构题，平衡树模板题，至于具体是哪种平衡树，只能说都可以，自己擅长哪个就在考试时用哪个。

前置知识

二叉搜索树和堆。
我们起码要知道，平衡树基于二叉搜索树，一个节点的左子树全都比当前节点小，一个节点的右子树全都比当前节点大。

写在前面，推荐原因

我在这里主要写 fhq Treap，这是一种无需旋转的 Treap 平衡树，而且支持可持久化，代码很短，明显好想。
不过在动态树实现时略差于 splay（其他时候基本都优于），在这里我们只用做普通平衡树。
在查找速度上弱于 AVL 这种严格平衡树，但只是常数上的问题，AVL 弱点也明显，就是在插入删除上十分缓慢，因为要经常旋转，而无旋的 fhq Treap 就会快上不少。
关于随机键值有小概率依旧退化成链的可能，可能性不大，在大数据下用随机数抽到链？我估计可以转博彩行业了... ...

较优的随机数生成算法

梅森旋转算法，虽然质量只是较高，但是效率很快，况且在算法竞赛上好写。
CPP
mt19937 randd(random_device{}());
其用线性反馈移位寄存器产生随机数，并且周期为 219937−12^{19937}−1（是一个梅森素数，因此而得名），说明这个寄存器是 1993719937 级的，他生成随机数的方式就是用这个寄存器一直移位旋转，以保证他的均匀分布。其代码很玄学，这里就不再放出来，有兴趣的可以自行学习。

具体操作

  • 定义
首先定义一棵树。
CPP
struct node{
	int l,r;
	int v;
	int rnd;
	int siz;
}t[100005];
  • 下放
再定义好一个下放函数。
修改时要随时下放哦~
一定注意不要写错，别忘了 +1+1，不然很难调的。
CPP
void push_up(int x){//size 的下传
	t[x].siz=t[t[x].l].siz+t[t[x].r].siz+1;
}

- 定义新节点
如果我们需要定义节点，我们需要这样操作。
```cpp
int newnode(int x){
	t[++tot].v=x;
	t[tot].rnd=rand();
	t[tot].siz=1;
	return tot;
}
很简单，因为要在插入函数中快速使用赋值，我们才 return tot; 的，事实上 void 也可以，后面 insertinsert 的时候我们要把当前点赋值为 tottot。
正片开始！
注意，我在讲解中省略了分裂操作的 int& l,int& r 两个参数，这个按照具体代码实现很好填，但是讲解时加上显得冗余。

插入

我们首先知道，一棵 fhq treap 是基于分裂和合并的，所以我们在插入的时候，需要先将整棵树分裂，插入后再合并，粗暴地说，就是把这棵树扒成两半，塞进去节点，再安起来。
就像下图这样。
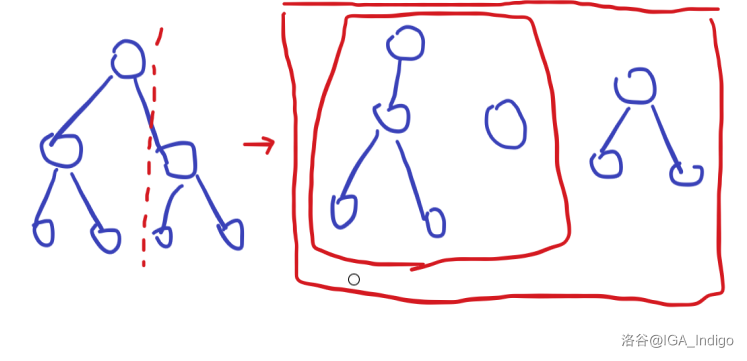（纯手绘，有点丑，凑合看）
先分裂成两棵树，然后将这个新节点先与切出来的左树合并，再把这颗混合树和右树合并。
下面我们具体讲讲分裂操作和合并操作。
  • 分裂
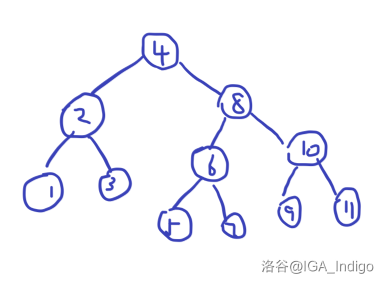
这是一颗普通的树，现在他要开始裂开了，我们要按照 66 这个值来分裂，也就是大于 66 的都在左边，小于等于 66 的都在右边。
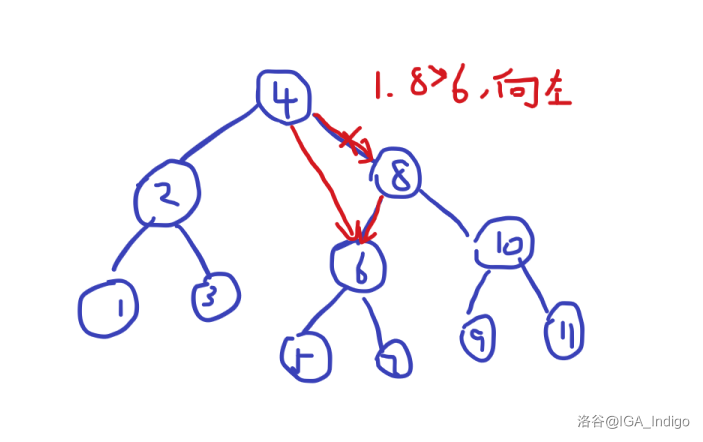
代表第一步：8>68 > 6，不是 1.8>61.8>6 啦！
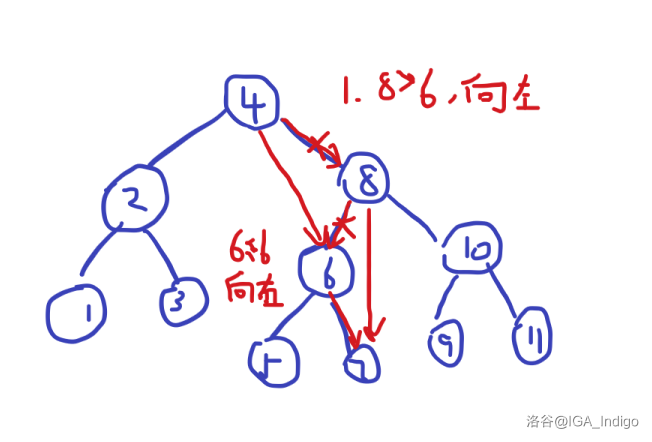
这样一步一步的向下找，然后最后建立一个新结点。将走过的边删掉，用遍历到的当前根节点连接当前节点。
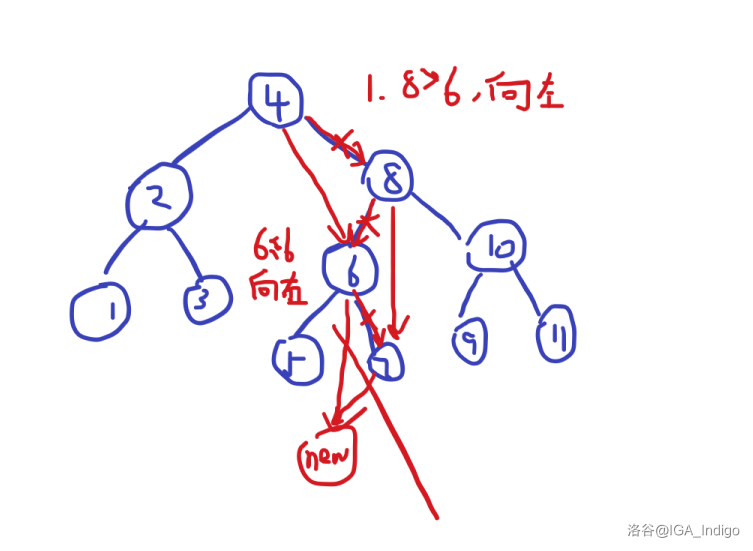
这里就忽略 7>67 > 6 吧（才不是忘写了）。
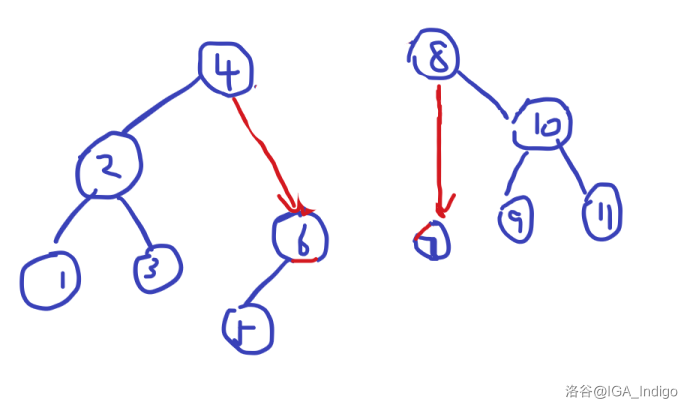
最后把所有连向新加节点的边全部删除，删掉所有无用的笔画，我们得到最终的图。
总结一下，我们实际是要找符合二叉搜索树的左子树和右子树给当前要求处理的这个点的 vv，把点传进来（从根节点开始往后查的子树结点）之后，先查一下这个点是否是空树，是的话直接返回走，不是的话按照 t[x].vt[x].v 的大小找他需要的子树，最后下放一下更新 lenlen 即可。
CPP
void split(int x,int v,int& l,int& r){
	if(!x){
		l=0;r=0;
		return ;
	}
	if(v>=t[x].v){
		l=x;
		split(t[x].r,v,t[x].r,r);
	}
	else{
		r=x;
		split(t[x].l,v,l,t[x].l);
	}
	push_up(x);
}
补充说明一点，分裂是整棵树分成两半，后期有大作用。
  • 合并
我们按照按照给的随机值来排序，小的那个成为合并后新树的树根，大的那个成为他的左/右子树，若其小的那个本身就有左/右子树，大的那个把他抢过来即可。
就像下图那样（我又要展示我的美术功力了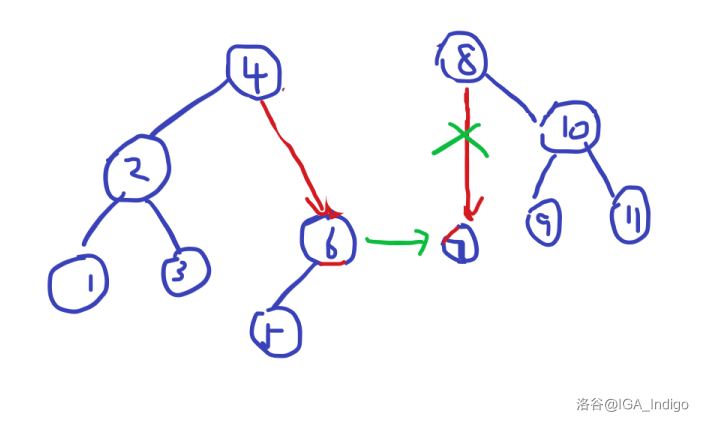）。 对于当前根节点，抢夺左儿子。 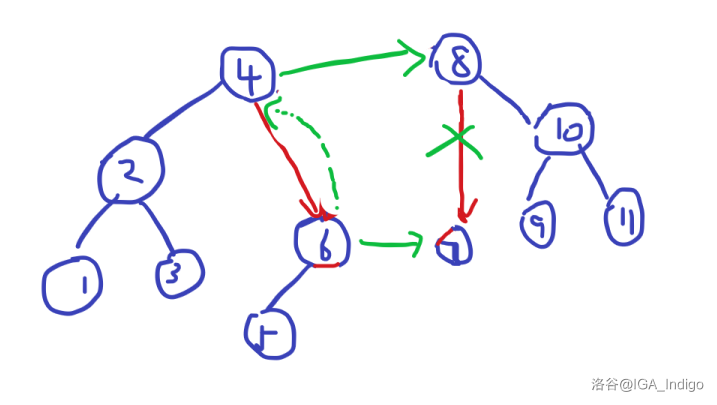然后回到自己父亲，连到右树的根节点。
不要忘记删除 44 和 66 之间的边。
配合代码食用一下吧。
CPP
int merge(int x,int y){
	if(!x||!y){
		return x+y;
	}
	if(t[x].rnd<t[y].rnd){
		t[x].r=merge(y,t[x].r);
		push_up(x);
		return x;
	}
	else{
		t[y].l=merge(x,t[y].l);
		push_up(y);
		return y ;
	}
注意一点，merge(x,y) 中我们能够满足左边全部节点的权值不大于 yy 的要求。为什么呢？我们可以看到，我们在函数中的判断要么是 xx 为根，yy 为他的右子树（if 语句里），要么是 yy 为根，xx 为他的左子树，递归实现，根据二叉排序树的性质，xx 的权值定然必须要比 yy 小的。
这时候我们可以学习插入了，插入讲究一个先分后合。
CPP
void insert(int v){
	int x,y;
	split(root,v,x,y);
	int xx=newnode(v);
	root=merge(merge(x,xx),y);
}
解释一点，rootroot 更新那里，不要以为分裂下去了之后就是在子树里面改了，分裂是整棵树分成两半，我们这里修改只是怕最上面的根节点 rndrnd 大被换下去。

删除

还是基于分裂和删除，我们直接看操作方式。
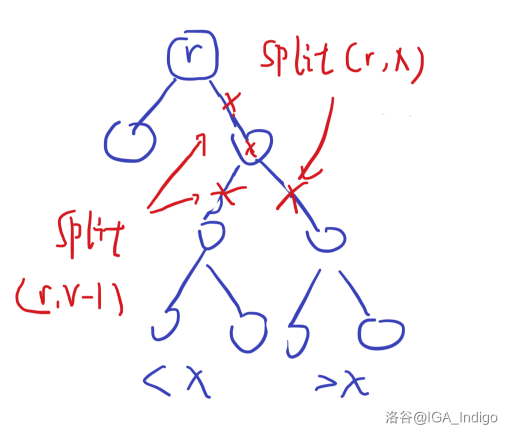
先从根节点按照 xx 分裂成三棵树，一颗大于 xx，一颗小于 xx，一颗等于 xx。
不管那颗等于 xx 的，将大于的和小于的合并。
代码有详解。
CPP
void delet(int v){
	int x,y,z;
	split(root,v,x,z);//先把最左边和最右边的子树找出来
	split(x,v-1,x,y);//然后查中间那个，split求的是第一个小于等于v-1的子树
	y=merge(t[y].l,t[y].r);//光删他一个点，子树留着
	root=merge(merge(x,y),z);//他仨重新合并，找到根节点 
}

求点 xx 的排名

点 xx 的排名就是分裂后小于 xx 的子树 size+1size+1。
我们这里直接调用 split(r,v-1) 即可。
千万记得求完答案要合并。
CPP
void qrank(int v){
	int x,y;
	split(root,v-1,x,y);
	cout<<t[x].siz+1<<endl;
	merge(x,y);
}

求排名为 kk 的点

按二叉搜索树的性质来搜。
  • 若当前节点左子树的 siz+1siz+1 恰好是 kk，那当前节点就是排名为 kk 的点，直接输出。
  • 若 k<siz+1k<siz+1，从左子树里面找排名为 kk 的点。
  • 若 k>siz+1k>siz+1，从右子树里面找排名为 k−siz−1k-siz-1 的点。
知道为什么有 +1+1 和 −1-1 吗？因为当前节点也是节点（这像话吗）。
CPP
void whorank(int x,int k){
	int siz=t[t[x].l].siz;
	if(k==siz+1){
		cout<<t[x].v<<endl;
		return ;
	}
	else if(k<=siz){
		whorank(t[x].l,k);
		return ;
	}
	else{
		whorank(t[x].r,k-siz-1);
		return ;
	}
}

前驱与后继

整个看下来，前驱与后继就 so easy 了。
  • 前驱
我们按照 v−1v-1 来分裂，输出比他小的树里最大值即可。
在找最大值的时候，我们可以在这棵树里面找排名为这棵树 sizsiz 的数是几。
最后别忘了把他们合并起来。
CPP
void qqq(int v){
	int x,y;
	split(root,v-1,x,y);
	whorank(x,t[x].siz);
	root=merge(x,y);
}
  • 后继
和前驱相反，按照 vv 来分裂，输出比他大的树里最小值。
这时候我们就要找大的那棵树里面排名第 11 的了。
CPP
void qhj(int v){
	int x,y;
	split(root,v,x,y);
	whorank(y,1);
	root=merge(x,y);
}

总结

写了这么多，总得有点总结。
是不是感觉平衡树也不是这么难？主要是要感谢 fhq，写下的平衡树简单快捷。
一定要注意，Treap 是对权值形成二叉搜索树，不要跟文艺平衡树搞混了。

Code

CPP
#include<bits/stdc++.h>
using namespace std;
mt19937 rnd(random_device{}());
struct node{
	int l,r;
	int v;
	int rnd;
	int siz;
}t[100005];
int tot=0,root=0;//现在结点的数量和根节点
void push_up(int x){//size 的下传
	t[x].siz=t[t[x].l].siz+t[t[x].r].siz+1;
}
int newnode(int x){
	t[++tot].v=x;
	t[tot].rnd=rnd();
	t[tot].siz=1;
	return tot;
}
void split(int x,int v,int& l,int& r){
	if(!x){
		l=0;
		r=0;
		return ;
	}
	if(v>=t[x].v){
		l=x;
		split(t[x].r,v,t[x].r,r);
	}
	else{
		r=x;
		split(t[x].l,v,l,t[x].l);
	}
	push_up(x);
}
int merge(int x,int y){
	if(!x||!y){
		return x+y;
	}
	if(t[x].rnd<t[y].rnd){
		t[x].r=merge(t[x].r,y);
		push_up(x);
		return x;
	}
	else{
		t[y].l=merge(x,t[y].l);
		push_up(y);
		return y;
	}
}
void insert(int v){
	int x,y;
	split(root,v,x,y);
	int xx=newnode(v);
	root=merge(merge(x,xx),y);
}
void delet(int v){
	int x,y,z;
	split(root,v,x,z);//先把最左边和最右边的子树找出来
	split(x,v-1,x,y);//然后查中间那个，split求的是第一个小于等于v-1的子树
	y=merge(t[y].l,t[y].r);//光删他一个点，子树留着
	root=merge(merge(x,y),z);//他仨重新合并，找到根节点 
}
void qrank(int v){
	int x,y;
	split(root,v-1,x,y);
	cout<<t[x].siz+1<<endl;
	merge(x,y);
}
void whorank(int x,int k){
	int siz=t[t[x].l].siz;
	if(k==siz+1){
		cout<<t[x].v<<endl;
		return ;
	}
	else if(k<=siz){
		whorank(t[x].l,k);
		return ;
	}
	else{
		whorank(t[x].r,k-siz-1);
		return ;
	}
}
void qqq(int v){
	int x,y;
	split(root,v-1,x,y);
	whorank(x,t[x].siz);
	root=merge(x,y);
}
void qhj(int v){
	int x,y;
	split(root,v,x,y);
	whorank(y,1);
	root=merge(x,y);
}
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		int op,x;
		cin>>op>>x;
		if(op==1){
			insert(x);
		}
		else if(op==2){
			delet(x);
		}
		else if(op==3){
			qrank(x);
		}
		else if(op==4){
			whorank(root,x);
		}
		else if(op==5){
			qqq(x);
		}
		else{
			qhj(x);
		}
	}
	return 0;
}

评论

共 2 条评论，欢迎与作者交流。

正在加载评论...