题解：CF2097B Baggage Claim

某梦姓机构在模拟赛中出过几乎一模一样的，怎么现在还是不会做呢？

首先如果存在相邻两个点（$p_{2i-1},p_{2i+1}$）的曼哈顿距离不是 $2$，直接输出 $0$ 结束了。然后我们考察这两个点中间的点是啥。

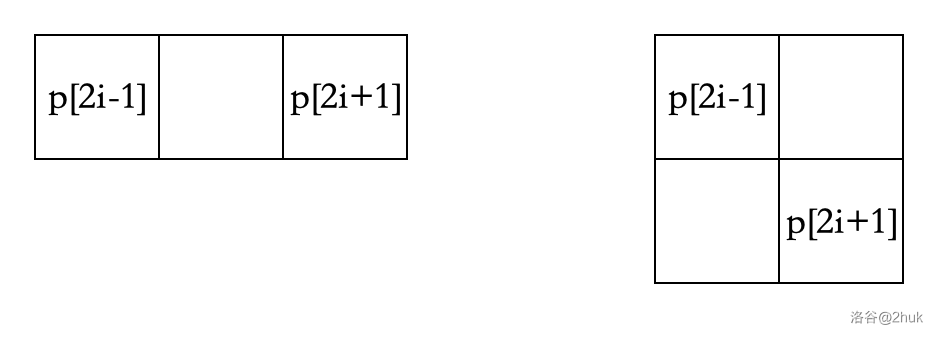
我们给所有可能成为中间的点编号（就是离散化）。得到两个数组 $a_i,b_i$，表示 $p_{2i-1},p_{2i+1}$ 这两个点中间的点编号一定是 $a_i$ 或 $b_i$。当然如果是左图的情况则 $a_i=b_i$。

现在问题变成了，对于每个 $i$，选择 $a_i,b_i$ 中的恰好一个数，使得选出的 $n$ 个数互不相同，求方案数。这样的答案再除以 $2$ 的第一种情况数次幂就是真正答案。

这个咋做呢？

既然是两个点，我们考虑建无向图 $a_i - b_i$。那么怎么体现两个点只能选一个，且这个点在全局只能选一次呢？

考虑转化成一个给无向图的边定向的问题。具体的，如果我们给这条边定向为 $a_i \to b_i$，则表示这个位置选 $b_i$。同理，如果是 $a_i \gets b_i$，表示这个位置选 $a_i$。那么一个点至多被选一次，等价于一个点的入度 $\le 1$。

我们考虑对图中每个连痛块单独计数。最后乘起来即可。

我们考虑这个连通块中的点数 $n$ 和边数 $m$。注意可能有自环。显然因为联通所以 $m \ge n - 1$。

那你不就做完了。