题解：AT_abc280_f [ABC280F] Pay or Receive

题目大意

有一张有向图，其中

\text{n}

个顶点，

\text{2m}

条边。第

\text{i}

条边连接

a_{i}

和

b_{i}

，其中从

a_{i}

到

b_{i}

的权值为

c_{i}

，从

b_{i}

到

a_{i}

的权值为

-c_{i}

。给出

Q

个问题：

从 $X_{i}$ 到 $Y_{i}$ 时的最大得分。
如果 $X_{i}$ 与 $Y_{i}$ 不在一个子图里，输出 nan。
如果 $X_{i}$ 到 $Y_{i}$ 的分数可以是无限，输出 inf。

注：本题解的子图可以理解为强连通分量。

思路

分析

这是‌最长路‌问题，根据题意，输出有

3

种情况。

‌第一种情况‌：需 $a_i$ 与 $b_i$ 在同一子图中。
‌第二种情况‌： $a_i$ 与 $b_i$ 不在同一子图，输出 nan。
‌第三种情况‌：子图存在正环，输出 inf。

解法

首先我们需要了解图的两个知识。

如下图，我们举个例子，我们问从 $1$ 号点到 $6$ 号点的最大距离是多少？很容易看出 $1$ 号点到 $6$ 号有两条路径，通过观察，我们易得，只要到终点的其中两条路径不相等，则这个子图是正环，也就是子图内的所有点的到图内任意点的距离都是可以无限刷分的。

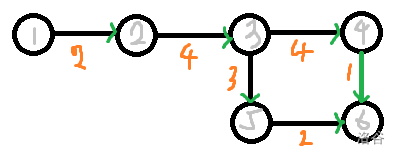
直接暴力搜图的肯定是不行的，所以我想到的一个类似前缀和的方法。还是那个图，如果我们问 $4$ 号点到 $5$ 号点的最长路，我们就可以用 $1$ 到 $5$ 号点的最长路减 $1$ 到 $4$ 号点的最长路，即 $l[y] - l[x]$ 其中 $l[]$ 为 $1$ 到 $x$ 点的最长路。

按上述枚举一遍边，最后输出答案。

代码

CPP

#include<bits/stdc++.h>
using namespace std;
// 表示从一个节点到另一个节点的有向边
struct node 
{	
    long long to, z;	 // to: 目标节点, z: 边的权值 
};

vector<node> v[1000009];
long long n, m, q, x, y, t;
long long l[1000009];  // l[]: 节点 i 在当前子图中的基准得分
long long j[1000009];  // j[]: 节点 i 所属的子图编号
long long cnt;         // cnt: 当前子图的编号
long long p[1000009];  // p[]: 标记子图 i 是否存在正环（可获得无限分数）
bool f[1000009];  

void dfs(long long dis)
{
    j[dis] = cnt;  
    f[dis] = true;  
    long long len = v[dis].size();  
    for(long long i = 0; i < len; i++)  // 遍历所有边
    {
        long long u = v[dis][i].to;  
        if(f[u] == false)  // 如果目标节点未被访问
        {
            l[u] = l[dis] + v[dis][i].z;  
            dfs(u);  
        }
        else if(l[u] != l[dis] + v[dis][i].z)  // 说明存在正环
            p[cnt] = 1;  // 标记当前子图存在正环
    }
    return ;
}

int main()
{
    scanf("%lld%lld%lld", &n, &m, &q); 
    for(long long i = 1; i <= m; i++) 
    {
        scanf("%lld%lld%lld", &x, &y, &t);
        node p; 
        p.to = y, p.z = t;  // 设置正向边（x->y，得分为 t）
        v[x].push_back(p); 
        p.to = x, p.z = -t;  // 设置反向边（y->x，得分为 -t）
        v[y].push_back(p); 
    }
    
    for(long long i = 1; i <= n; i++)  // 遍历所有节点，处理各个子图
        if(f[i] == false)  // 如果节点 i 未被访问（属于新的子图）
        {    
            cnt++;  // 子图编号加 1
            dfs(i);  // 从节点 i 开始深度优先搜索
        }
    
    while(q--)
    {
        scanf("%lld%lld", &x, &y); 
        if(j[x] != j[y])  // 如果两个节点不在同一个子图中
            printf("nan\n");
        else if(p[j[x]])  // 存在正环
            printf("inf\n");
        else printf("%lld\n", l[y] - l[x]); 
    }
    return 0;
}

题解：AT_abc280_f [ABC280F] Pay or Receive

文章操作

题目大意

思路

分析

解法

代码

相关推荐

评论

题解：AT_abc280_f [ABC280F] Pay or Receive