CF207B3 Military Trainings 题解

首先容易想到把序列复制一遍，破环为链，每个询问即查询子段答案。

设 $f_i$ 能从 $j=x$ 或 $j=y$ 转移而来，考虑一个贪心。

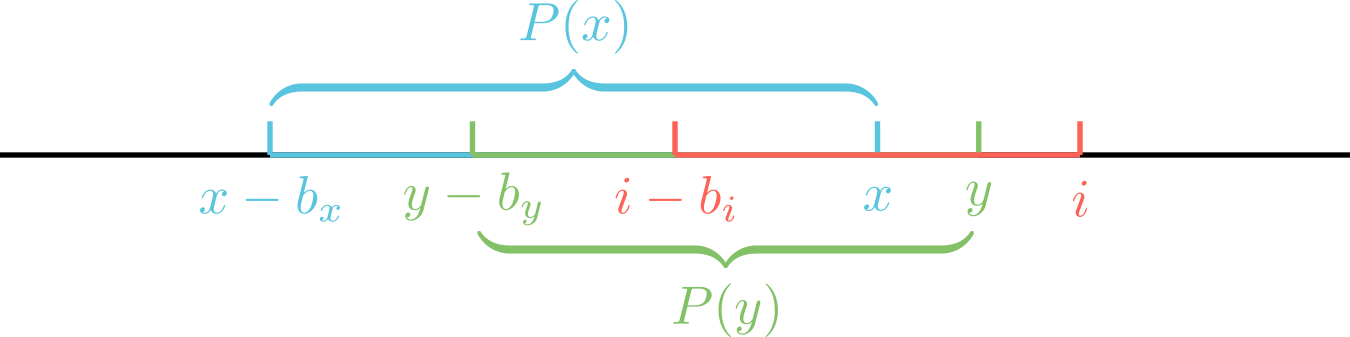
其中 $P(k)$ 表示 $f_k$ 能从哪些点转移而来，即 $P(k)=[k-p_k,k-1]$。

由于 $k-1\in P(k)$ 恒成立，我们无需考虑 $[i-p_i,k-1]$ 这段区间的贡献。而 $[y-p_y,i-p_i]\subseteq[x-p_x,i-p_i]$，即所有能转移到 $y$ 的点都能转移到 $x$，因此选择从 $x$ 转移而来即可。这也就是说，从 $k-p_k$ 较小的 $k$ 转移来是不劣的。用 ST 表维护之，复杂度 $\mathcal{O}(n\log n+\text{ans})$。

你交了一发，并发现这个东西在模拟赛过了。可以使用倍增预处理出跳 $2^n$ 步能跳到哪，优化成 $\mathcal{O}(n\log n)$。