注 :为便于理解,笔者对概念和结论进行了简化和不严谨概括。关于抽象代数之群论,见
抽象代数学习笔记 ,其中轨道-稳定子定理是结论 4.2。
什么是群 简单地说,群可以理解为一族描述操作的元素
{ g 1 , g 2 , ⋯ , g n } \{g_1, g_2, \cdots, g_n\} { g 1 , g 2 , ⋯ , g n } 构成的集合
G G G ,满足三个条件:
操作之间可以进行复合,且依然得到 G G G
存在什么都不做的操作。
操作可逆。
群
二元组
( G , ⋆ ) (G, \star) ( G , ⋆ ) 称为
群 ,若集合
G G G 在二元运算
⋆ : G × G → G \star: G\times G\to G ⋆ : G × G → G 下:
满足结合律 a ⋆ ( b ⋆ c ) = ( a ⋆ b ) ⋆ c a\star (b \star c) = (a\star b)\star c a ⋆ ( b ⋆ c ) = ( a ⋆ b ) ⋆ c
存在单位元 e e e a ∈ G a\in G a ∈ G e ⋆ a = a ⋆ e = a e\star a = a\star e = a e ⋆ a = a ⋆ e = a
任意 a ∈ G a\in G a ∈ G a − 1 a ^ {-1} a − 1 a ⋆ a − 1 = a − 1 ⋆ a = e a\star a ^ {-1} = a ^ {-1}\star a = e a ⋆ a − 1 = a − 1 ⋆ a = e
可以证明 逆元唯一 。
一般
e e e 记为
1 1 1 且省略
⋆ \star ⋆ 不写。
因为逆元存在且唯一,所以群是具有
消去律 的。即若
g h = g ′ h gh = g'h g h = g ′ h ,则
g = g ′ g = g' g = g ′ 。
群作用 “操作” 体现为
G G G 的每个元素可以作用在满足条件的集合
A A A 的每个元素上,依然得到
A A A 中的元素,称为
G G G 作用在
A A A 上。例如,
A A A 是所有长度为
4 4 4 且值域为
[ 1 , 3 ] [1, 3] [ 1 , 3 ] 的整数序列,
g i g_i g i 表示向右循环移位
i i i 个下标。设
a = ( 1 , 2 , 3 , 3 ) a = (1, 2, 3, 3) a = ( 1 , 2 , 3 , 3 ) ,则
g 1 a = ( 3 , 1 , 2 , 3 ) g_1a = (3, 1, 2, 3) g 1 a = ( 3 , 1 , 2 , 3 ) 。
群作用
映射
⋅ : G × A → A \cdot : G\times A\to A ⋅ : G × A → A 是群
G G G 在集合
A A A 上的
群作用 ,若:
对任意 g 1 , g 2 ∈ G g_1, g_2\in G g 1 , g 2 ∈ G a ∈ A a\in A a ∈ A g 1 ⋅ ( g 2 ⋅ a ) = ( g 1 g 2 ) ⋅ a g_1\cdot (g_2 \cdot a) = (g_1g_2) \cdot a g 1 ⋅ ( g 2 ⋅ a ) = ( g 1 g 2 ) ⋅ a
对任意 a ∈ A a\in A a ∈ A 1 ⋅ a = a 1\cdot a = a 1 ⋅ a = a
可以证明
g g g 作用在不同的元素上,得到的元素也是不同的。将
g : a ↦ g ⋅ a g : a\mapsto g\cdot a g : a ↦ g ⋅ a 看成
A → A A\to A A → A 的映射,那么
g g g 有逆映射
g − 1 g ^ {-1} g − 1 ,因为
( g g − 1 ) ⋅ a = 1 ⋅ a = a (gg ^ {-1}) \cdot a = 1\cdot a = a ( g g − 1 ) ⋅ a = 1 ⋅ a = a 。因此,
g g g 一定是双射。
群其实是把 “变换“ 这个概念抽象成符号之后得到的具有一些基本性质的一族变换。一个变换的性质体现于它作用在集合上产生的效果,而群的性质体现于变换之间满足的特定关系。例如,在上例中,
g i = g 1 i g_i = g_1 ^ i g i = g 1 i ,
g 0 = 1 g_0 = 1 g 0 = 1 。
为什么要学习群 我们常说的 “群描述对称性” 是指一些常见的群可以由作用对象的对称性得出。例如,保持正方形及其定向不变(即不允许翻转)的群是四阶循环群
Z 4 = { g 0 , g 1 , g 2 , g 3 } Z_4 = \{g_0, g_1, g_2, g_3\} Z 4 = { g 0 , g 1 , g 2 , g 3 } ,其中
g k g_k g k 表示沿中心顺时针旋转
k π 2 \frac {k\pi} 2 2 kπ (如果允许翻转,则是八阶二面体群
D 8 D_8 D 8 )。将正方形的四个角用任意排列标号,那么一个标号和它的循环移位所对应的正方形相等,我们认为这些正方形处于相同的 “等价类”,称为
轨道 。
轨道 orbit
考虑
G G G 作用在
A A A 上(作用不一定唯一)。对
a ∈ A a\in A a ∈ A ,
{ g ⋅ a ∣ g ∈ G } \{g\cdot a\mid g\in G\} { g ⋅ a ∣ g ∈ G } 称为
a a a 的
轨道 。
群公理所保证的良好性质使得群作用的轨道是等价关系。简单地说,如果
b = g ⋅ a b = g\cdot a b = g ⋅ a 在
a a a 的轨道内,那么
a = g − 1 ⋅ b a = g ^ {-1}\cdot b a = g − 1 ⋅ b 也在
b b b 的轨道内。所以
A A A 中两个元素的轨道要么不交,要么相等。又因为每个元素属于它自己的轨道,所以在给定作用下,
G G G 将
A A A 划分(每个元素恰属于一个集合)为了若干轨道
O 1 , O 2 , ⋯ , O k \mathcal O_1, \mathcal O_2, \cdots, \mathcal O_k O 1 , O 2 , ⋯ , O k ,满足轨道内的每个元素的轨道等于该轨道。
所以,对称性的说法是先有等价类才有了群,群描述了等价类,也就是对象的对称性。
OI 中的群论问题一般是反过来的,形如
给定 G , A G, A G , A G G G A A A 。例如,计算长为
n n n 且值域为
[ 1 , m ] [1, m] [ 1 , m ] 的整数序列的数量,其中序列循环同构,即如果
a a a 可以通过循环移位得到
b b b ,则认为
a , b a, b a , b 相等。这里,
G G G 是所有可能的循环移位,
A A A 是所有长为
n n n 且值域为
[ 1 , m ] [1, m] [ 1 , m ] 的整数序列。两个序列在相同等价类当且仅当它们可以通过循环移位相互得到,因此等价类数量就是题目所求的答案。
轨道数量怎么求呢?
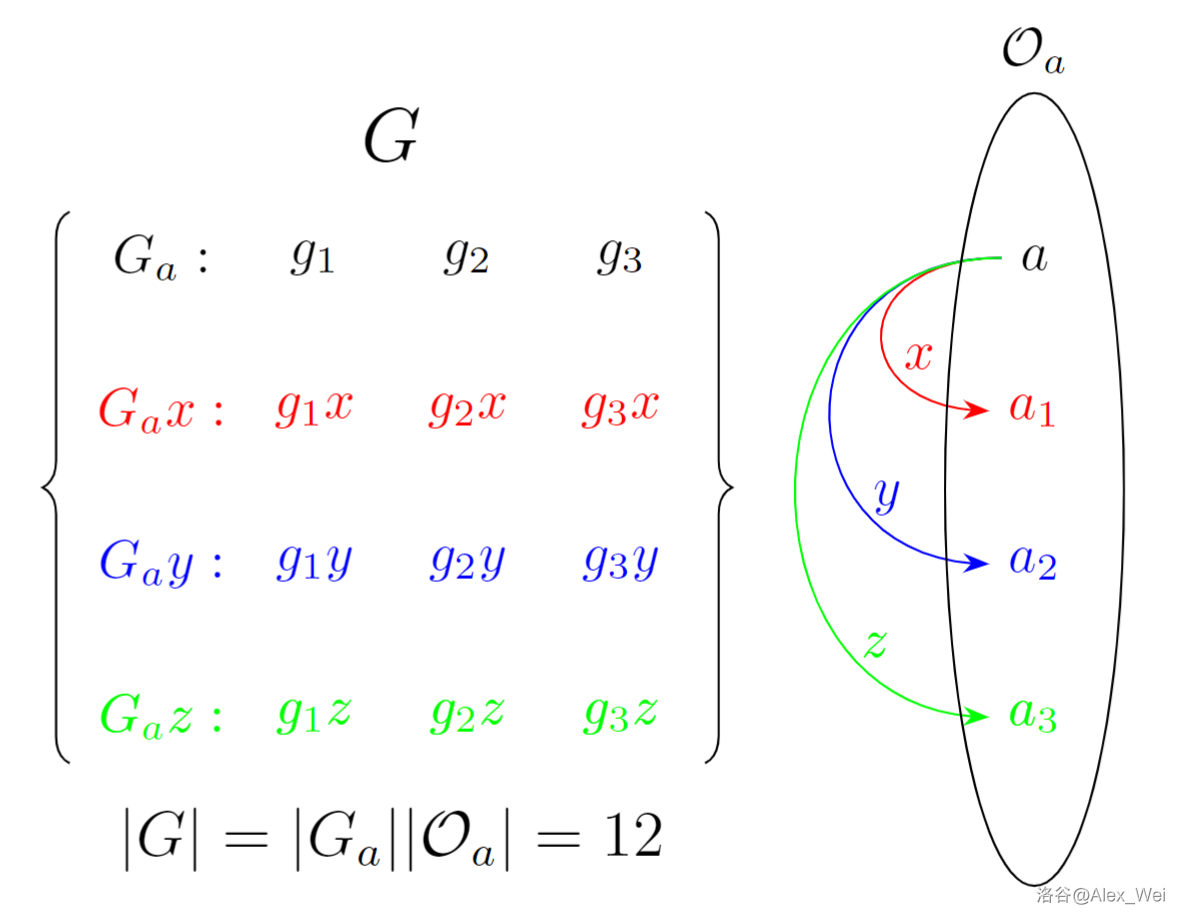
轨道-稳定子定理 考虑
G G G 作用在
A A A 上,每个
a ∈ A a\in A a ∈ A 有轨道
O a \mathcal O_a O a 。设
G a = { g ∣ g ⋅ a = a } G_a = \{g\mid g\cdot a = a\} G a = { g ∣ g ⋅ a = a } 表示所有保持
a a a 不变的
G G G 的变换(称为
稳定子,稳定化子 stabilizer ),则
∣ O a ∣ ∣ G a ∣ = ∣ G ∣ . |\mathcal O_a| |G_a| = |G|. ∣ O a ∣∣ G a ∣ = ∣ G ∣. 可以想象一个乘法表:
G a G_a G a 的变换写在每列的上边,对每个
b ∈ O a b\in \mathcal O_a b ∈ O a 任选变换
g b g_b g b 使得
g b ⋅ a = b g_b\cdot a = b g b ⋅ a = b 写在每行的左边。每行每列的交点填入对应两个变换的复合(乘的顺序要一致,例如都是上边复合左边),则整个表恰好可以乘出
G G G 的所有变换。
所有保持
a a a 不动的变换
G a G_a G a 复合任意一个把
a a a 作用到
b ∈ O a b\in \mathcal O_a b ∈ O a 的变换,均可得到所有把
a a a 作用到
b b b 的变换
G a → b G_{a\to b} G a → b ,且这些变换两两不同,即
∣ G a ∣ = ∣ G a → b ∣ |G_a| = |G_{a\to b}| ∣ G a ∣ = ∣ G a → b ∣ 。
为什么两两不同:由消去律,若 g 1 x = g 2 x g_1x = g_2x g 1 x = g 2 x g 1 = g 2 g_1 = g_2 g 1 = g 2 ∣ G a ∣ ≤ ∣ G a → b ∣ |G_a| \leq |G_{a\to b}| ∣ G a ∣ ≤ ∣ G a → b ∣
为什么是所有:把上述分析倒过来可得 ∣ G a → b ∣ ≤ ∣ G a ∣ |G_{a\to b}| \leq |G_a| ∣ G a → b ∣ ≤ ∣ G a ∣ G a → b G_{a\to b} G a → b g ∈ G b → a g\in G_{b\to a} g ∈ G b → a a a a ∣ G a → b ∣ ≤ ∣ G a ∣ |G_{a\to b}|\leq |G_a| ∣ G a → b ∣ ≤ ∣ G a ∣
G G G 的每个变换将
a a a 变成其轨道中的某个元素,所以每个元素都落在乘法表中,且恰好出现一次。
Burnside 引理 考虑
G G G 作用在
A A A 上,我们希望计算轨道的数量。对每个轨道
O i \mathcal O_i O i 和
a i ∈ O i a_i\in \mathcal O_i a i ∈ O i ,根据轨道-稳定子定理,
∣ O i ∣ ∣ G a i ∣ = ∣ G ∣ |\mathcal O_i||G_{a_i}| = |G| ∣ O i ∣∣ G a i ∣ = ∣ G ∣ 。又因为轨道内所有元素的稳定子数量相同(所有元素的轨道相等,用轨道-稳定子定理即可),所以
∑ a i ∈ O i ∣ G a i ∣ = ∣ G ∣ , \sum_{a_i\in \mathcal O_i} |G_{a_i}| = |G|, a i ∈ O i ∑ ∣ G a i ∣ = ∣ G ∣ , 即一个轨道内所有元素的稳定子数量之和等于
∣ G ∣ |G| ∣ G ∣ 。
每个元素恰属于一个轨道,所以我们将所有元素的稳定子数量加起来,所得结果就是对每个轨道都求出其中所有元素的稳定子数量之和后再求和。因此,将结果除以
∣ G ∣ |G| ∣ G ∣ 就是轨道数量
k k k 。
k = 1 ∣ G ∣ ∑ a ∈ A ∣ G a ∣ . k = \frac {1} {|G|}\sum_{a\in A} |G_a|. k = ∣ G ∣ 1 a ∈ A ∑ ∣ G a ∣. 但是一般而言
A A A 是很大的集合(例如,所有长为
n n n 且值域为
[ 1 , m ] [1, m] [ 1 , m ] 的整数序列),所以这个公式还不够好用。
我们换一种求和方式。本来是对每个元素求有多少个变换使得它不变,考虑转换视角,对每个变换求有多少元素在该变换下不变。对
g ∈ G g\in G g ∈ G ,设
f ( g ) f(g) f ( g ) 表示使得
g ⋅ a = a g\cdot a = a g ⋅ a = a (
不动点 )的
a a a 的数量,则
∑ a ∈ A G a = ∑ g ∈ G f ( g ) \sum_{a\in A} G_a = \sum_{g\in G} f(g) ∑ a ∈ A G a = ∑ g ∈ G f ( g ) 。
∑ a ∈ A ∣ G a ∣ = ∑ a ∈ A ∑ g ∈ G [ g ⋅ a = a ] = ∑ g ∈ G ∑ a ∈ A [ g ⋅ a = a ] = ∑ g ∈ G f ( g ) . \sum_{a\in A} |G_a| = \sum_{a\in A} \sum_{g\in G} [g\cdot a = a] = \sum_{g\in G} \sum_{a\in A} [g\cdot a = a] = \sum_{g\in G} f(g). a ∈ A ∑ ∣ G a ∣ = a ∈ A ∑ g ∈ G ∑ [ g ⋅ a = a ] = g ∈ G ∑ a ∈ A ∑ [ g ⋅ a = a ] = g ∈ G ∑ f ( g ) .
于是我们得到了 Burnside 引理
k = 1 ∣ G ∣ ∑ g ∈ G f ( g ) . k = \frac 1 {|G|}\sum_{g\in G} f(g). k = ∣ G ∣ 1 g ∈ G ∑ f ( g ) . 如果序列只是循环同构,那么
G G G 的大小仅有
n n n ,这使得 Burnside 引理比前一个公式好用了很多。
Burnside 引理的公式中有
1 n \frac 1 n n 1 ,但
n n n 在模意义下可能没有逆元。解决方法有两个(本质相同):
将每个数写成 a n + b an + b an + b n n n b b b 0 0 0 b b b b b b
设模数为 p p p n × p n\times p n × p n n n n n n n n n gcd ( n , p ) × p \gcd(n, p)\times p g cd( n , p ) × p __int128 大小的数相乘。
Pólya 计数定理 Pólya 计数定理是 Burnside 引理的特例,这里只介绍简化版本。
依然考虑先前的例子,计算长为
n n n 且值域为
[ 1 , m ] [1, m] [ 1 , m ] 的整数序列在循环同构下的数量。此时
G = { g 0 , g 1 , ⋯ , g n − 1 } G = \{g_0, g_1, \cdots, g_{n - 1}\} G = { g 0 , g 1 , ⋯ , g n − 1 } 是所有长为
n n n 的循环移位。根据 Burnside 引理,计算
f ( g i ) f(g_i) f ( g i ) 。
g i g_i g i 表示向右循环移位
i i i 个下标。这是一个排列,可以分解为若干个环,每个元素移动到出边指向的位置。如果
a a a 在
g i g_i g i 下不变,那么对于
g i g_i g i 的每个环,都需要满足
a a a 在环的所有位置上相等。因此,每个环有
m m m 种方案,总方案数(不动点数量)为
m c ( g i ) m ^ {c(g_i)} m c ( g i ) ,其中
c ( g ) c(g) c ( g ) 表示排列
g g g 的环的数量。根据经典的数论知识(见
1.7 小节),
c ( g i ) = gcd ( n , i ) c(g_i) = \gcd(n, i) c ( g i ) = g cd( n , i ) 。
更一般地,对于给定置换群(即一些排列构成的群)
G G G ,如果认为两个能通过
G G G 中的排列相互得到的序列是等价的,那么不同的序列数量为
1 ∣ G ∣ ∑ g ∈ G m c ( g ) . \frac 1 {|G|} \sum_{g\in G} m ^ {c(g)}. ∣ G ∣ 1 g ∈ G ∑ m c ( g ) . 称为 Pólya 计数定理 。
由 Burnside 引理,只需证明
f ( g ) = m c ( g ) f(g) = m ^ {c(g)} f ( g ) = m c ( g ) 。若一组染色方案在
g g g 下是不动点,那么
g g g 的每个环的所有元素的颜色相同。每个环有
m m m 种染色方案,由乘法原理即得。
□ \square □
例题 Pólya 定理的简单应用。旋转
k k k 个下标的排列的环数为
gcd ( n , k ) \gcd(n, k) g cd( n , k ) ,所以答案为
∑ i = 0 n − 1 n gcd ( i , n ) − 1 \sum_{i = 0} ^ {n - 1} n ^ {\gcd(i, n) - 1} ∑ i = 0 n − 1 n g c d ( i , n ) − 1 。
∑ d ∣ n n d − 1 ∑ i = 0 n − 1 [ gcd ( i , n ) = d ] = ∑ d ∣ n n d − 1 φ ( n d ) . \sum_{d\mid n} n ^ {d - 1} \sum_{i = 0} ^ {n - 1} [\gcd(i, n) = d] = \sum_{d\mid n} n ^ {d - 1} \varphi\left(\frac n d\right). d ∣ n ∑ n d − 1 i = 0 ∑ n − 1 [ g cd( i , n ) = d ] = d ∣ n ∑ n d − 1 φ ( d n ) . 直接计算即可,时间复杂度
O ( T d ( n ) n ) \mathcal{O}(Td(n)\sqrt n) O ( T d ( n ) n ) 。
代码 。
问题的两部分是独立的。使用 Burnside 引理算出有多少种可能的戒指,再求出长度为
N N N 的环的相邻不同的染色方案数(颜色数量是戒指的数量)。这里,我们认为特殊纪念品在序列的第
N N N 个位置和第
1 1 1 个位置之间。就算两个不同的序列在循环移位下相等,它们也对应不同的项链,因为特殊纪念品的位置不同。
用
C C C 种颜色给长度为
N N N 的环染色,要求相邻不同,方案数为
( C − 1 ) N + ( − 1 ) N ( C − 1 ) (C - 1) ^ N + (-1) ^ N (C - 1) ( C − 1 ) N + ( − 1 ) N ( C − 1 ) 。这个是经典问题。
时间复杂度
O ( M + log N ) \mathcal{O}(\sqrt M + \log N) O ( M + log N ) 。
代码 。
怎么这么多项链题,和 P5233 一样是二合一。
∑ 1 ≤ i ≤ j ≤ k ≤ a [ gcd ( i , j , k ) = 1 ] . \sum_{1\leq i\leq j\leq k\leq a} [\gcd(i, j, k) = 1]. 1 ≤ i ≤ j ≤ k ≤ a ∑ [ g cd( i , j , k ) = 1 ] . 经典莫比乌斯反演,得到
m = ∑ d ∣ a μ ( d ) ∑ 1 ≤ i ≤ j ≤ k ≤ a d 1 = ∑ d ∣ a μ ( d ) ( a d 3 ) . \begin{aligned}
m & = \sum_{d \mid a} \mu(d) \sum_{1\leq i\leq j\leq k\leq \frac a d} 1 \\
& = \sum_{d\mid a} \mu (d) \binom {\frac a d} 3.
\end{aligned} m = d ∣ a ∑ μ ( d ) 1 ≤ i ≤ j ≤ k ≤ d a ∑ 1 = d ∣ a ∑ μ ( d ) ( 3 d a ) . 循环同构,考虑 Burnside 引理,计算旋转
i i i 下标之后相等的项链数量,要求项链在模
d = gcd ( n , i ) d = \gcd(n, i) d = g cd( n , i ) 相同的下标上的珠子是相同的。题目还要求相邻不同,结合前一个限制,等价于仅考虑前
d d d 个位置构成的环时相邻不同。这部分和 P5233 一样,直接套公式
( m − 1 ) n + ( − 1 ) n ( m − 1 ) (m - 1) ^ n + (-1) ^ n(m - 1) ( m − 1 ) n + ( − 1 ) n ( m − 1 ) 即可。注意
n n n 可能是
p p p 的倍数,所以我们使用之前提到的技巧,将答案写成
a n + b an + b an + b 的形式,或对
p 2 p ^ 2 p 2 取模。
时间复杂度
O ( n + a ) \mathcal{O}(\sqrt n + a) O ( n + a ) 。
代码 。
题意就差把 Burnside 引理写在脸上了:给定一个置换群,求所有可能的牌堆在该置换群的作用下形成的等价类数量。
“任意多次洗牌都可用这 m m m
“对每种洗牌法,都存在一种洗牌法使得能回到原状态” 保证排列有逆排列。
使用 Burnside 引理,求每个排列的不动点数量。每个环上的颜色要相同,且每个颜色的数量需要满足题目限制。简单背包即可。
时间复杂度
O ( m S r S b S g ) \mathcal{O}(mS_rS_bS_g) O ( m S r S b S g ) 。
代码 。
因为图在排列下同构,所以答案是所有
m m m 种颜色的
n n n 元无向完全图在
n n n 元对称群(所有
n n n 阶排列构成的群)作用下的等价类数量。考虑 Burnside 引理。
对于每个排列
p p p ,考虑
p p p 的不动点数量。
对于排列的每个环,
( 0 , k ) (0, k) ( 0 , k ) 和
( 1 , k + 1 ) (1, k + 1) ( 1 , k + 1 ) 的颜色相同,以此类推。于是对每个
1 ≤ k ≤ c 2 1\leq k\leq \frac c 2 1 ≤ k ≤ 2 c ,所有距离为
k k k 的边的颜色相同,其中
c c c 是环长。环内部的 “自由度” 为
⌊ c 2 ⌋ \lfloor \frac c 2 \rfloor ⌊ 2 c ⌋ 。
对于环长分别为
c 1 c_1 c 1 和
c 2 c_2 c 2 的环之间的边,固定
k k k ,对所有
i i i ,
( i m o d c 1 , ( k + i ) m o d c 2 ) (i\bmod c_1, (k + i) \bmod c_2) ( i mod c 1 , ( k + i ) mod c 2 ) 的颜色相同。第一个位置每次回到
0 0 0 ,第二个位置会跳
c 1 c_1 c 1 步,所以总共形成
gcd ( c 1 , c 2 ) \gcd(c_1, c_2) g cd( c 1 , c 2 ) 个子环,环之间的 “自由度” 为
gcd ( c 1 , c 2 ) \gcd(c_1, c_2) g cd( c 1 , c 2 ) 。
注意到我们只关心环长形成的集合,所以直接枚举
n n n 的所有分拆,算出对应的不动点数量以及排列数量,相乘后求和再除以
n ! n! n ! 即可。对于环长集合
c 1 , ⋯ , c k c_1, \cdots, c_k c 1 , ⋯ , c k ,不动点数量已经给出。根据经典组合结论,排列数量为
n ! ( ∏ i = 1 k c i ) ( ∏ j = 1 n d j ! ) , \frac {n!} {\left(\prod_{i = 1} ^ k c_i\right)\left(\prod_{j = 1} ^ n d_j!\right)}, ( ∏ i = 1 k c i ) ( ∏ j = 1 n d j ! ) n ! , 其中
d j d_j d j 表示长度为
j j j 的环的数量。
每次取出 c i c_i c i n ! ( n − c i ) ! \frac {n!} {(n - c_i)!} ( n − c i )! n ! c i c_i c i c i c_i c i n ! ∏ i = 1 k c i \frac {n!} {\prod_{i = 1} ^ k c_i} ∏ i = 1 k c i n !
相同大小的环之间是无序的,但我们依次确定每个环导致相同大小的环之间有序,所以要除掉 d j ! d_j! d j !
时间复杂度
O ( P ( n ) n 2 ) \mathcal{O}(P(n) n ^ 2) O ( P ( n ) n 2 ) ,其中
P ( n ) P(n) P ( n ) 表示
n n n 的分拆数。
代码 。
是 P4128 的
m = 2 m = 2 m = 2 ,
p = 997 p = 997 p = 997 版本。
变换是所有使得图同构的点置换,作用的集合是所有可能的染色。暴力枚举排列判定图同构,再使用 Burnside 引理即可。
时间复杂度
O ( n ! n 2 ) \mathcal{O}(n!n ^ 2) O ( n ! n 2 ) 。
代码 。
问题要求价值的期望,即每个本质不同排列的连通块数量之和除以本质不同排列的数量。
Part I
先考虑本质不同排列的数量。因为序列循环同构,所以自然地想到 Burnside 引理。对每个
0 ≤ i < n 0\leq i < n 0 ≤ i < n ,求出循环移位
i i i 个下标的不动点数量,也就是有多少个序列在该变换下是不变的。
根据经典数论结论(步长与子环,
1.7),旋转
i i i 个下标的置换
g i g_i g i 会将大小为
n n n 的环分成
d = gcd ( n , i ) d = \gcd (n, i) d = g cd( n , i ) 个大小为
n d \frac n d d n 的环。为了让序列在该变换下是不动点,每个环上的所有点的数字应当相同。例如当
i = 2 i = 2 i = 2 ,
n = 6 n = 6 n = 6 时,只有满足
a 1 = a 3 = a 5 a_1 = a_3 = a_5 a 1 = a 3 = a 5 且
a 2 = a 4 = a 6 a_2 = a_4 = a_6 a 2 = a 4 = a 6 的
{ a i } \{a_i\} { a i } 是变换的不动点。所以,固定
a 1 ∼ d a_{1\sim d} a 1 ∼ d 即可确定整个序列。
方案数是多少呢?设
L = n d L = \frac n d L = d n ,也就是每个环的长度。因为环上的数相同,所以每个数的出现次数都应是
L L L 的倍数。设
c j c_j c j 表示
j j j 在给定的
{ a i } \{a_i\} { a i } 当中的出现次数,则
L ∣ c j L\mid c_j L ∣ c j ,否则无解。在此基础上,枚举每个数在哪些环,得到方案数
f L = ( d c 1 L , c 2 L , ⋯ , c n L ) . f_L = \binom d {\frac {c_1} L, \frac {c_2} L, \cdots, \frac {c_n} L}. f L = ( L c 1 , L c 2 , ⋯ , L c n d ) . 注意方案数
f L f_L f L 和
i i i 的值无关,只和
d d d 有关。
此外,
d d d 还需满足
L ∣ gcd ( c 1 , ⋯ , c n ) L\mid \gcd(c_1, \cdots, c_n) L ∣ g cd( c 1 , ⋯ , c n ) 。这部分的时间复杂度为
O ( n d ( n ) ) \mathcal{O}(nd(n)) O ( n d ( n )) 。
如何做到线性
设
k k k 表示
{ a i } \{a_i\} { a i } 有多少个不同的数。
因为
L ≤ min j = 1 n c j ≤ n k L\leq \min_{j = 1} ^ n c_j \leq \frac n k L ≤ min j = 1 n c j ≤ k n ,所以最多有
n k \frac n k k n 个合法的
d d d 。而预处理阶乘和阶乘逆元后计算
f L f_L f L 的复杂度为
O ( k ) \mathcal{O}(k) O ( k ) ,所以可线性求出所有需要的
f L f_L f L ,再乘以有多少个
gcd ( i , n ) = d \gcd(i, n) = d g cd( i , n ) = d 。这是经典结论,要求
i i i 除以
d d d 之后和
n d \frac n d d n 互质,即
φ ( n d ) \varphi(\frac n d) φ ( d n ) ,线性筛出欧拉函数即可。
Part II
连通块数量等于有多少对相邻两个数不同。我们枚举每对相邻的位置,算出有多少个本质不同的排列在这个地方产生了贡献。注意这要求至少有两个环,那么相邻两个位置一定在不同的环。
直接枚举这两个数
x , y ( x ≠ y ) x, y\ (x\neq y) x , y ( x = y ) ,
x x x 在前,
y y y 在后,有
n n n 组相邻的位置可以填,填完之后对应的环就固定了。剩下的环依然是随便填,方案数为
( d − 2 c 1 L , ⋯ , c x L − 1 , ⋯ , c y L − 1 , ⋯ , c n L ) = f d c x c y d ( d − 1 ) L 2 . \binom {d - 2} {\frac {c_1} L, \cdots, \frac {c_x} L - 1, \cdots, \frac {c_y} L - 1, \cdots, \frac {c_n} L} = \frac {f_d c_xc_y} {d(d - 1)L ^ 2}. ( L c 1 , ⋯ , L c x − 1 , ⋯ , L c y − 1 , ⋯ , L c n d − 2 ) = d ( d − 1 ) L 2 f d c x c y . 而
∑ x ≠ y c x c y = ( ∑ x = 1 n c x ) 2 − ∑ x = 1 n c x 2 , \sum_{x\neq y} c_xc_y = \left(\sum_{x = 1} ^ n c_x\right) ^ 2 - \sum_{x = 1} ^ n c_x ^ 2, x = y ∑ c x c y = ( x = 1 ∑ n c x ) 2 − x = 1 ∑ n c x 2 , 所以
g d = n f d d ( d − 1 ) L 2 ( n 2 − ∑ j = 1 n c j 2 ) . g_d = \frac {nf_d} {d(d - 1)L ^ 2}\left(n ^ 2 - \sum_{j = 1} ^ n c_j ^ 2\right). g d = d ( d − 1 ) L 2 n f d ( n 2 − j = 1 ∑ n c j 2 ) . 时间复杂度视实现精细程度为
O ( n d ( n ) ) \mathcal{O}(nd(n)) O ( n d ( n )) 或
O ( n ) \mathcal{O}(n) O ( n ) 。
首先考虑刻画合法装饰方式。
通过打表找规律或简单分析可知:
如果一个位置填入 4 4 4 4 4 4 4 4 4 4 4 4 1 , 2 1, 2 1 , 2 3 3 3
如果一个位置填入 3 3 3 3 3 3 3 3 3
2 2 2
用相邻的两个
1 1 1 覆盖一些位置(但不能和其它的
1 1 1 连通),使得剩下的位置形成若干个环。根据总度数的限制容易证明只有以下四种情况:
CPP 222222
222211
211222
221221
221221
2221
2121
2122
每若干行一定是以上元素的不断重复,不同的若干行之间由
3 3 3 连通块隔开。
题目要求循环同构,Burnside 引理 + DP 即可。因为
12 12 12 一定是一行的循环节,所以对于循环移位
i i i ,我们只关心
gcd ( i , C , 12 ) \gcd(i, C, 12) g cd( i , C , 12 ) 。
时间复杂度
O ( n ) \mathcal{O}(n) O ( n ) 。
代码 。
对于
2 a × 2 b 2 ^ a \times 2 ^ b 2 a × 2 b 的矩阵,第
i i i 行第
j j j 列在内存中的下标为
i × 2 b + j i \times 2 ^ b + j i × 2 b + j 。把每个位置的下标看成
a + b a + b a + b 位的二进制数,则转置相当于将这个数向右循环移位
b b b 位。
因为一个长为
c c c 的环需要
c − 1 c - 1 c − 1 次交换操作归位,所以答案为
2 a + b 2 ^ {a + b} 2 a + b 减去环的数量。后者是
a + b a + b a + b 位二进制数在循环移位
k b ( 0 ≤ k < n gcd ( n , b ) ) kb\ (0\leq k < \frac n {\gcd(n, b)}) kb ( 0 ≤ k < g c d ( n , b ) n ) 位构成的群的作用下形成的等价类数量。
使用 Burnside 引理,得到答案为
1 n g ∑ d ∣ n g 2 n d φ ( d ) . \frac {1} {\frac n g} \sum_{d\mid \frac n g} 2 ^ {\frac n d}\varphi(d). g n 1 d ∣ g n ∑ 2 d n φ ( d ) . 其中
n = a + b n = a + b n = a + b 。时间复杂度
O ( n log n + T d ( n ) ) \mathcal{O}(n\log n + Td(n)) O ( n log n + T d ( n )) 。
代码 。
使用 Burnside 引理,求循环移位的不动点数量。问题转化为给定
L , m , k L, m, k L , m , k ,求长度为
L L L 的环放
m m m 个
1 1 1 且不能有超过
k k k 个
1 1 1 相邻的方案数。
先考虑链的情况。这是经典问题,容斥,钦定
i i i 个
0 0 0 前面有连续
k + 1 k + 1 k + 1 个
1 1 1 ,总方案数为
∑ i ≥ 0 ( − 1 ) i ( L − i ( k + 1 ) L − m ) ( L − m + 1 i ) , \sum_{i \geq 0} (-1) ^ {i}\binom {L - i(k + 1)} {L - m} \binom {L - m + 1} i, i ≥ 0 ∑ ( − 1 ) i ( L − m L − i ( k + 1 ) ) ( i L − m + 1 ) , 其中第二个组合数的上指标要加
1 1 1 ,是考虑到末尾有连续
k + 1 k + 1 k + 1 个
1 1 1 的情况。
i i i 的上界为
L k \frac L k k L 级别。
对于环,枚举开头和结尾的
1 1 1 连续段的总长,有
k k k 种可能性。于是计算一组
L , m , k L, m, k L , m , k 的时间为
O ( L ) \mathcal{O}(L) O ( L ) 。
因为
L ∣ n L\mid n L ∣ n ,所以时间复杂度为
n n n 的约数和,即
O ( σ ( n ) ) \mathcal{O}(\sigma(n)) O ( σ ( n )) 。可以证明
σ ( n ) = O ( n log log n ) \sigma(n) = \mathcal{O}(n\log \log n) σ ( n ) = O ( n log log n ) 。
好题。
编号无关,枚举所有环长可重集,要求每个点的度数都是偶数。
在环内部,两端距离为
k k k 的边要么同时出现,要么同时不出现。只有当
k = c 2 k = \frac c 2 k = 2 c 时会改变所有点的奇偶性,其它时候均成环。
在环之间,一共有
d = gcd ( c 1 , c 2 ) d = \gcd(c_1, c_2) d = g cd( c 1 , c 2 ) 组,每组让大小为
c i c_i c i 的环上每个点的度数增加
c 1 c 2 d c i \frac {c_1c_2} {d c_i} d c i c 1 c 2 ,于是每组边会改变一个环或者两个环上所有点的奇偶性。
问题转化为:每个点可以被操作
d i d_i d i 次,每条边可以被操作
e j e_j e j 次(操作两个端点),求所有点被操作偶数次的方案数。根据整体的奇偶性要求,可知每个点被单独操作的次数之和为偶数。此时,对每个连通块(
e j > 0 e_j > 0 e j > 0 的边形成的连通块),选择一棵生成树,不在生成树上的边随意,则树边有唯一方案使得满足条件。
因此,设连通块有
C C C 个点,
D = ∑ d i D = \sum d_i D = ∑ d i ,
E = ∑ e j E = \sum e_j E = ∑ e j ,则自由度为
max ( 0 , D − 1 ) + ( E − ( C − 1 ) ) \max(0, D - 1) + (E - (C - 1)) max ( 0 , D − 1 ) + ( E − ( C − 1 )) 。
时间复杂度
O ( P ( n ) n 2 ) \mathcal{O}(P(n)n ^ 2) O ( P ( n ) n 2 ) 。
代码 。
CHANGE LOG
2025.8.1:重构文章。
2025.9.5:加入例题 P13227。
参考资料 全文
例题