专栏文章

题解：P11846 [USACO25FEB] Transforming Pairs P

TTwilight_star
P11846题解参与者 6已保存评论 5

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
5 条
当前快照
1 份
快照标识符
@mipj3sdm
此快照首次捕获于
2025/12/03 12:50
3 个月前
此快照最后确认于
2025/12/03 12:50
3 个月前
查看原文
题目链接
首先先讨论弱化版 P11841 [USACO25FEB] Transforming Pairs S。
弱化版保证 a,b,c,d>0a,b,c,d>0。从 (a,b)(a,b) 开始推有点难，因为很难判断到底要进行多少次各个操作。于是考虑从 (c,d)(c,d) 开始倒推。
我们发现，(c,d)(c,d) 的前置状态是确定的：
  • 当 c>dc>d 时，只能从 (c−d,d)(c-d,d) 转移过来。
  • 当 c<dc<d 时，只能从 (c,d−c)(c,d-c) 转移过来。
  • 当 c=dc=d 时，能从 (c,0)(c,0) 或 (0,d)(0,d) 转移过来，但是弱化版讨论范围在正整数，所以暂时不考虑。
这个前置状态很像用更相减损法求 gcd⁡\gcd 的过程。但是更相减损法是 O(V)O(V) 的，VV 为值域大小。考虑换成更快的欧几里得法求 gcd⁡\gcd 的过程。将多次 c←c−dc\gets c-d 和多次 d←d−cd\gets d-c 操作作为一组放在一起讨论。
每一次操作钦定 c>dc>d，若不符则 swap(a,b)⁡,swap(c,d)⁡\operatorname{swap(a,b)},\operatorname{swap(c,d)}。然后判断是否有 b=db=d 且 cc 减去若干个 dd 后能等于 aa 即可。时间复杂度为 O(log⁡V)O(\log V)。
现在考虑本题。我们按 a,b,c,da,b,c,d 的正负进行分类讨论：

1. a,ba,b 同号 (包含 a=0a=0 或 b=0b=0)

此时如果 a<0a<0 或 b<0b<0，就把 a,b,c,da,b,c,d 全部变为它自己的相反数。
于是一定有 a,b≥0a,b\ge 0。考虑用类似弱化版的做法。但是需要进行更改，因为弱化版不用考虑 00 的情况，本题这里需要考虑。
回顾弱化版，当 c=dc=d 时，会将 cc 或 dd 减为 00。换成欧几里得法，就是 c mod d=0c \bmod d=0 时，会将 c,dc,d 其中一个减为 00。则进行分类讨论：
  • 如果将 cc 减为 00
    则最终 (c,d)(c,d) 会成为 (0,d)(0,d)。于是 a=0a=0 且 b=db=d 则可以成功。
  • 如果将 dd 减为 00
    则一定是将 (c,d)(c,d) 减为 (d,d)(d,d) 然后再一步减为 (d,0)(d,0)。所以 a=da=d 且 b=0b=0 时也是可以的。
代码如下：
CPP
int calc(int a,int b,int c,int d)
{//计算 a,b>=0 时的答案
	if(c<0||d<0) return -1;
	if(a==c&&b==d) return 0;
	int res=0;
	while(c!=0&&d!=0)
	{
		if(a==c&&b==d) return res;
		if(c<d) swap(c,d),swap(a,b);
		if(b==d&&c>=a&&c%d==a%d) return res+(c-a)/d;//能否把c删成a 
		if(c%d==0&&((a==0&&b==d)||(a==d&&b==0))) return res+c/d;//删成0是否满足要求 
		res+=c/d;
		c%=d;
	}
	if(a==c&&b==d) return res;
	return -1;
}
void solve()
{
	a=read(),b=read(),c=read(),d=read();
	if(a==c&&b==d) return printf("0\n"),void();
	if(a<=0&&b<=0) a=-a,b=-b,c=-c,d=-d;
	if(a<0) swap(a,b),swap(c,d); 
	if(a>=0&&b>=0)//a,b同号 
	{
		if(c<0||d<0) return printf("-1\n"),void();
		return printf("%lld\n",calc(a,b,c,d)),void();	
	}
}

2. a,ba,b 异号，c,dc,d 异号

我们会发现，在操作途中，当 a,ba,b 从异号变成了同号，则不可能再变成异号。
于是当 a,ca,c 不同号，b,db,d 不同号时则无解。
剩下的情况仅剩 a,ca,c 同号，b,db,d 同号。我们模拟从 (a,b)(a,b) 出发的操作，因为不能让数改变符号，所以每一次只能是让绝对值大的数加上绝对值小的数。并且操作途中 a,ba,b 的绝对值会不断减小。
举个例子，现在 (a,b)(a,b) 满足 ∣a∣>∣b∣,a>0,b<0|a|>|b|,a>0,b<0，此时则一定变成 (a+b,b)(a+b,b)，则只看绝对值的话会从 (∣a∣,∣b∣)→(∣a∣−∣b∣,∣b∣)(|a|,|b|)\to (|a|-|b|,|b|)。这样只看绝对值是不是有点像上种情况的从 c,dc,d 倒推的情形。
于是这种情况的答案为上种情况 (c,−d)→(a,−b)(c,-d)\to (a,-b) 的答案。（钦定 c>0c>0）
CPP
//a,b异号，c,d异号，已保证a>0
if(c<0&&d>0) return printf("-1\n"),void();
if(c>=0&&d<=0) return printf("%lld\n",calc(c,-d,a,-b)),void();

3. a,ba,b 异号，c,dc,d 同号

现在需要考虑 a,ba,b 从异号变为同号的过程。先钦定 a,c,d>0,b<0a,c,d>0,b<0。如果不符可以通过交换和取相反数满足。
我们把它搬到平面直角坐标系上讨论。存在两个坐标 (a,b),(c,d)(a,b),(c,d)。那么无论是从 (a,b)(a,b) 开始推还是从 (c,d)(c,d) 开始倒推都是不断在向 xx 轴靠近。直到某一次操作我们让 (a,b)(a,b) 变为同号。
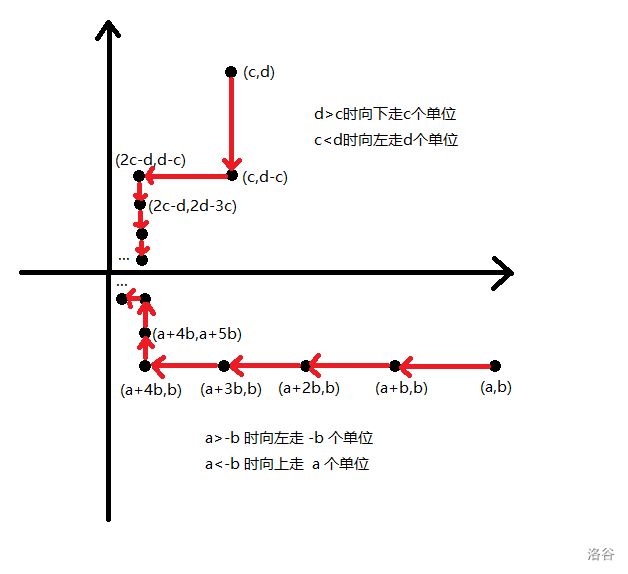
其实什么时候让 a,ba,b 变为同号是我们自己选择的。当 a>−ba>-b 时，如果不想跨过 xx 轴则走到 (a+b,b)(a+b,b)，但是如果我们向跨过 xx 轴，则可以直接走到 (a,a+b)(a,a+b)。
如下图，蓝色边为跨过 xx 轴的转移边。
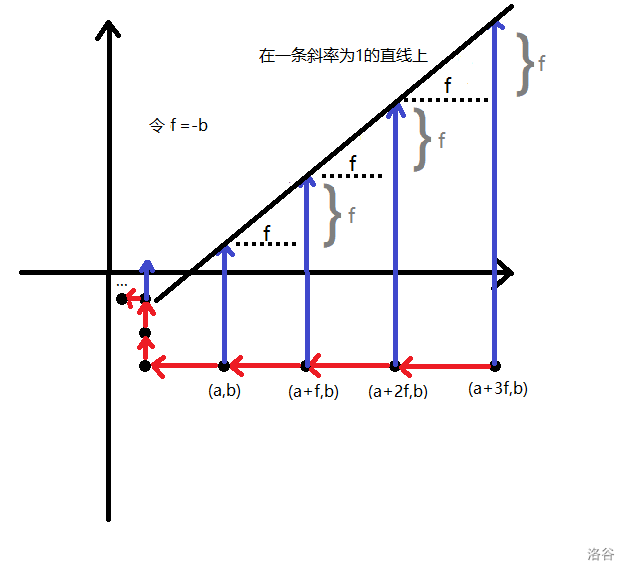
我们会发现，对于一段连续的向左的一组转移，我们可以从中选择一个点向上转移，并且向上转移后的落点在一条斜率为 11 的直线上。
但是，有些落点是无法到达 (c,d)(c,d) 的。所以我们还要求出可以到达 (c,d)(c,d) 的所有点，再与所有落点取交集，才是真正合法的落点。
设 (x,y)(x,y) 为真正合法的落点之一，根据落点的定义，则一定有 x<yx<y。所以从 (c,d)(c,d) 开始倒推的话， 到达 (x,y)(x,y) 下一步应该向左走。于是将所有向左走的点与所有落点取交即可。
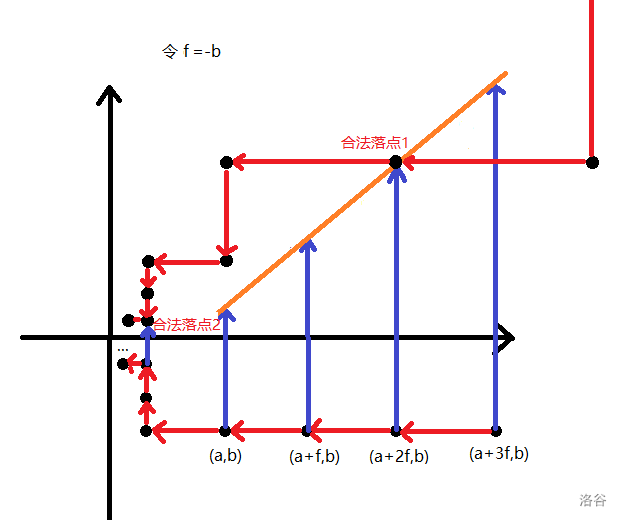
于是枚举 (c,d)(c,d) 倒推向左走的每一组，并预处理出 (c,d)(c,d) 到这一组第一个点的操作次数。再枚举 (a,b)(a,b) 正推向左走的每一组，并预处理出 (a,b)(a,b) 到这一组第一个点的操作次数。
然后对交点计算总的操作次数即可。
注意不要漏掉落点在 xx 轴上的情况。
总时间复杂度 O(qlog⁡2V)O(q\log^2V)。
具体判断条件见代码：
CPP
//a,b异号，c,d同号
if(c<=0&&d<=0) a=-a,b=-b,c=-c,d=-d; 
if(a<0) swap(a,b),swap(c,d);

vector< array<int,3> > q;
for(int x=c,y=d,num=0;x>0&&y>0;)
{
  if(y>=x) num+=y/x,y%=x;
  else q.push_back({y,x,num}),num+=x/y,x%=y;
}//预处理 (c,d) 倒推时到达每一个向左组的操作次数 

int ans=inf,num=0;//num为(a,b)到当前组的 
while(a>0&&b<0)
{
  if(a+b==0)//向上走到坐标轴上 
  {
    ans=min(ans,num+1+calc2(a,0,c,d)); //calc2(a,b,c,d): 当calc(a,b,c,d)==-1时为inf，否则为calc(a,b,c,d) 
    break;
  }
  if(a+b<0)//向上走，不用考虑穿过坐标轴 
  {
    num+=(-b)/a;
    b=-((-b)%a);
    continue;
  }
  //向左走 
  for(auto i:q)//枚举 (c,d) 倒推途中向左转移的组 
  { 
    int y=i[0],mx=i[1];
    if(y<=a+b&&(a-y)%(-b)==0)//(a,a+b)为本组最右的落点 
    {
      int k=(a+b-y)/(-b);//本组第几个点 
      int x=a+k*b;//落点横坐标 
      if(x<=mx&&(mx-x)%y==0) ans=min(ans,num+i[2]+1+k+(mx-x)/y);//落点能在(c,d)路径上 
    }
   } 
  if(a%(-b)==0) ans=min(ans,num+a/(-b)+calc2(-b,0,c,d));//向上拐，走到x轴上 
  num+=a/(-b);
  a%=(-b);
}
if(a>=0&&b>=0) ans=min(ans,num+calc2(a,b,c,d));
if(ans>=inf) printf("-1\n");
else write(ans),putchar('\n');

评论

共 5 条评论，欢迎与作者交流。

正在加载评论...