2025.3.29

修正一处错别字。

2025.4.29

修改了后记。

树链剖分求 LCA

前言

树剖求 LCA 的基本思想是将树按一定方式剖分成链，随后便可以在链上进行快速操作求得 LCA，单次求解的时间复杂度在

O(\log{n})

。

树剖基本内容

在讲解如何进行树剖求 LCA 前，我们需要先了解树剖的一些相关定义以及性质（有过了解的同学可以自行跳过这部分）。

定义

重儿子：某个父节点的儿子中，子树大小（也就是子树中节点最多的）最大的节点。（同时规定一个节点的重儿子只有一个）
轻儿子：某个父节点的儿子中，非重儿子的节点。
重边：父节点与其重儿子连成的边。
轻边：父节点与其轻儿子连成的边。
重链：由多条重边连成的链。（叶子节点单独成链）

放一张图辅助理解：

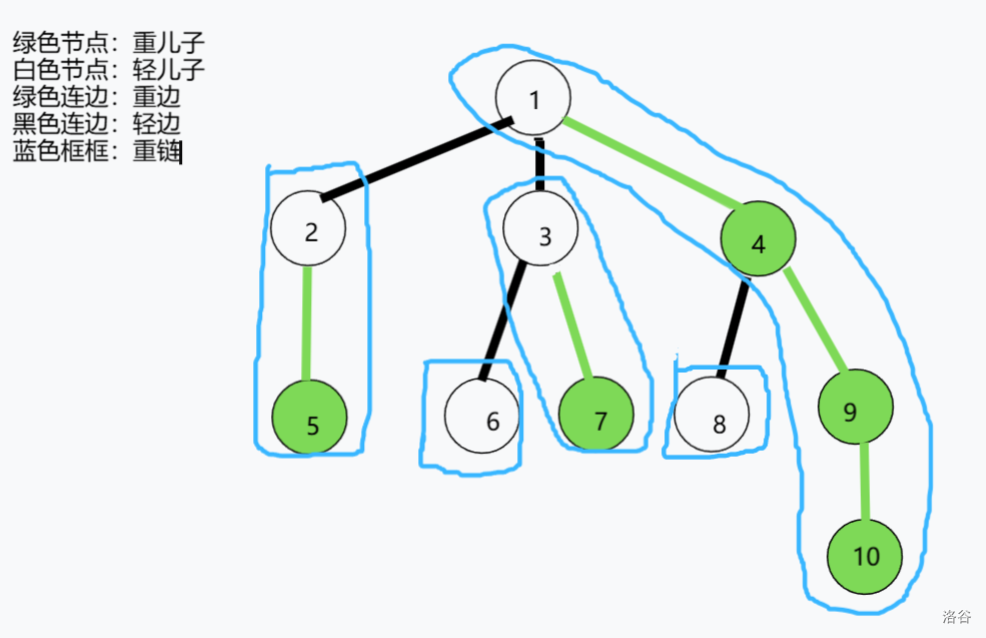
上图内容不难从定义推得，我挑取一部分详细解释一下（认为自己能够完全理解定义的同学可以跳过了）：

$1$ 节点的重儿子是 $4$ （其子树大小为 $4$ 并且无法在 $1$ 节点的其他儿子节点找到子树大小更大的）。
$2$ 节点的重儿子是 $5$ （因为只有一个儿子，所以你当然无法找到第二个子树大小更大的）。
$3$ 节点的重儿子可以在 $6$ 或者 $7$ 中任意选得，因为它们的子树大小是一样的，但我们需要保证一个子树的重儿子只有一个。
$1$ 节点到 $10$ 节点连成的重链中 $4$ 是 $1$ 的重儿子， $9$ 是 $4$ 的重儿子， $10$ 是 $9$ 的重儿子。
节点 $6$ 没有重儿子，单独成链（因为我们要让树全部剖分成链，如果没有重边连成重链，就单独成链），同理，节点 $8$ 也是。

性质

我们再次观察上图，不难发现有如下性质：

当前节点 $x$ 每次向下走一条轻边到达轻儿子 $y$ ，自身的子树大小至少除以 $2$ 。（否则 $y$ 就应该变为 $x$ 的重儿子）
每条重链的链顶一定是轻儿子。
任意两点的路径可以被不超过 $\log{n}$ 条链覆盖。（可以从性质第一条推导）

至此，树剖的基本定义和性质都已讲解完毕，接下来趁热打铁，具体看看我们究竟是如何进行链上的操作，快速求出两点的最近公共祖先的。

求解 LCA

操作流程

假设我们现在已经求得各节点的重儿子，并且知道了如何剖分这颗树，并把每个点

i

所在链的链顶记录进了

top[i]

。

在树上我们随便找两个点，这两个点的编号我们分别假设为变量

x

和变量

y

，如果我们现在想求得点

x

和点

y

的 LCA，我们需要每次查看这两个点是否在同一条链上，即

top[x]

是否等于

top[y]

，如果不等于，就让链顶深度更深的点跳出这个链，也就是跳到链顶的父节点，再次判断是否在同一条链上，直到它们跳到了同一条链，此时深度更浅的点就是我们想求得的 LCA。

如下图，模拟了点

13

和点

9

的 LCA 求解过程：

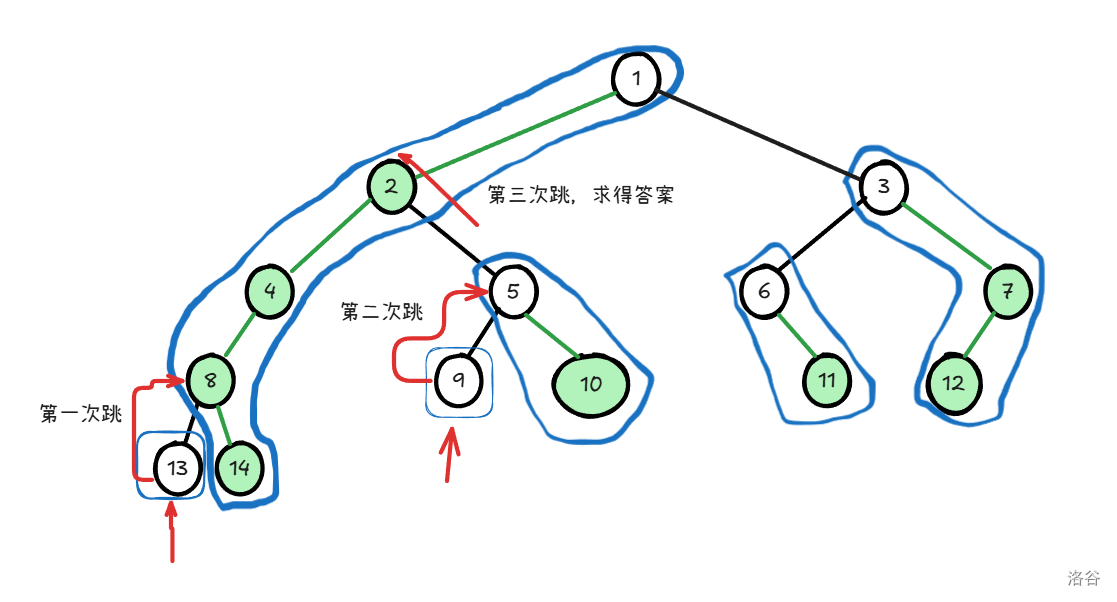
单次操作的时间复杂度

由性质三可以知道，任意两点间的路径至多被

\log{n}

条链覆盖，所以我们的单次链操作求解 LCA 的时间复杂度是在

O(\log{n})

级别的。

具体代码实现

想要实现树剖求解 LCA，我们的核心代码需要三部分：两遍 dfs 和求解 LCA 的函数。

dfs1()：用于求解整颗树各节点的：子树大小 $siz[i]$ 、深度 $dep[i]$ 、父节点 $fa[i]$ 、重儿子 $hson[i]$ 。
dfs2()：用于求解每个节点所在链的链顶 $top[i]$ 。
LCA()：按照之前讲解的流程求解 LCA。

第一遍 dfs

遍历了整棵树求解节点信息，时间复杂度

O(n)

。

CPP

//       当前节点  父节点 
void dfs1(int x,int f){
	siz[x]=1;//siz数组先初始化为1，表示目前自身大小为1 
	fa[x]=f;//记录父节点 
	dep[x]=dep[f]+1;//深度比父节点深1 
	for(int i=head[x];i;i=e[i].next){//遍历子节点 
		int y=e[i].to;
		if(y!=f){//注意别遍历回去了 
			dfs1(y,x); 
			siz[x]+=siz[y];//递归回来时，子节点的大小已经被计算完毕，直接加给父节点
			//每次递归判断是否能够更新重儿子节点 
			if(siz[hson[x]]<siz[y] || !hson[x]){
				hson[x]=y;
			}
		}
	}
}

第二遍 dfs

注意我们求解各节点所在链的链顶时，有重儿子要先遍历重儿子，直到找不到重儿子再返回。

这是因为沿着重边一路走下去的节点一定在同一条重链，其链顶是一样的，如果找不到重儿子，则说明该重链结束了，需要重新传入链顶参数进行新重链的求解。同样遍历了一遍整棵树，时间复杂度

O(n)

。

CPP

//     当前节点  链顶 
void dfs2(int x,int t){
	top[x]=t;//记录当前节点所在链的链顶 
	if(!hson[x]) return ;//如果找不到重儿子就返回 
	else dfs2(hson[x],t);//继续求解当前重链
	//递归后说明重链已经走完，接下来遍历轻儿子 
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		//这里的判断很容易理解，不能走到父节点还需要满足是轻儿子 
		if(y!=fa[x] && y!=hson[x]){
			dfs2(y,y);//根据性质，轻儿子就是当前新重链的链顶 
		}
	}
}

LCA 函数

上文已经把求解过程描述得很清楚了，具体细节看代码吧。

CPP

int LCA(int x,int y){
	//如果不在同一条链上 
	while(top[x]!=top[y]){
		//选择链顶深度更深的那个点跳上来 
		if(dep[top[x]]<dep[top[y]]){
			swap(x,y);
		}
		//跳出当前链 
		x=fa[top[x]];
	}
	//如果在一条链上，此时深度更浅的节点就是两个点的LCA 
	return dep[x]<dep[y]?x:y;
	//给不会三目运算符的小朋友解释一下，上面那行的意思是
	/*if(dep[x]<dep[y]){
		return x;
	}
	else{
		return y;
	}*/ 
}

总时间复杂度

因为两次 dfs 都是

O(n)

的，单次求解 LCA 的时间复杂度是

O(\log{n})

的，一共

m

次操作，故本题的总时间复杂度是

O(n+m\log{n})

的，常数很小，实际运行的速度十分可观。

完整代码

CPP

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
struct node{
	int next,to;
}e[N<<1];
int tot,head[N];
int dep[N],siz[N],hson[N],fa[N];
int top[N];
int n,m,s;
void add(int x,int y){
	e[++tot].to=y;
	e[tot].next=head[x];
	head[x]=tot;
}
void dfs1(int x,int f){
	siz[x]=1;
	fa[x]=f;
	dep[x]=dep[f]+1;
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		if(y!=f){
			dfs1(y,x);
			siz[x]+=siz[y];
			if(siz[hson[x]]<siz[y] || !hson[x]){
				hson[x]=y;
			}
		}
	}
}
void dfs2(int x,int t){
	top[x]=t;
	if(!hson[x])return ;
	dfs2(hson[x],t);
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		if(y!=fa[x] && y!=hson[x]){
			dfs2(y,y);
		}
	}
}
int LCA(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]]){
			swap(x,y);
		}
		x=fa[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin>>n>>m>>s;
	for(int i=1;i<n;i++){
		int x,y;
		cin>>x>>y;
		add(x,y);
		add(y,x);
	}
	dfs1(s,0);
	dfs2(s,s);
	for(int i=1;i<=m;i++){
		int a,b;
		cin>>a>>b;
		cout<<LCA(a,b)<<'\n';
	}
	return 0;
}

后记

树链剖分的用途不仅仅是用来求最近公共祖先的，其更大的价值体现在能够快速地进行树上的修改与查询操作，学有余力的同学接下来可以查看我的这篇题解：题解：P3384 【模板】重链剖分/树链剖分来进行进一步的学习。

至此所有内容已经讲解完毕，笔者力求语言简洁直观，希望大家看到这篇题解都能有所收获，若有不足之处，欢迎私信批评指出，笔者一定认真倾听。

谢谢大家，完结撒花。

题解：P3379 【模板】最近公共祖先（LCA）

文章操作