专栏文章
题解:P13118 [GCJ 2019 #2] Contransmutation
P13118题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @mimzz6g5
- 此快照首次捕获于
- 2025/12/01 18:19 3 个月前
- 此快照最后确认于
- 2025/12/01 18:19 3 个月前
题解:P13118 [GCJ 2019 #2] Contransmutation
Solution
注意到一个强连通分量内的所有元素都可以集中到任意一个节点上,即强连通分量中的每一个点都等价,容易想到先跑缩点。
于是我们得到了一个 DAG,因此要使一个节点(强连通分量)达到最大值,应该让所有能到达它的点都“分裂”,也就是说我们需要跑拓扑排序。现在我们考虑跑到某个强连通分量时,它满足什么条件会达到数量无限。
- 该强连通分量的某个父亲是无穷。
- 该强连通分量里有值,且其内部的边数大于点数。(这意味着有一个点的两个儿子都指向分量内,所以可以无限复制)
- 该强连通分量的某个父亲满足其内有值,且其内部的边数等于点数。(这意味着这个父亲是一个简单环,可以一直向儿子复制)
对于其他情况,直接将当前强连通分量的值加到儿子上即可。
Attention
值得注意的是,这道题可以出现这样的情况:
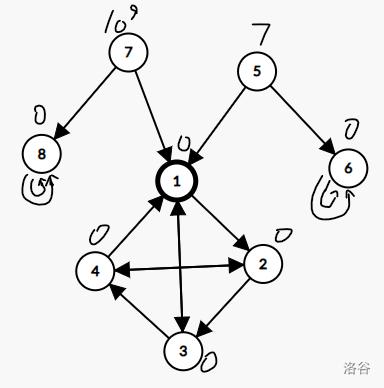

如果关于取模的操作处理不当,可能会导致答案误判为 。
Code
CPP#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200005,M = 1000000007;
int t,n,a[N],b[N],c[N],low[N],dfn[N],id[N],cnt,col,p[N],sz[N],in[N],ans[N];
bool isn[N];
vector<int>vec[N],tec[N];
stack<int>s;
void Tarjan(int u)
{
dfn[u] = low[u] = ++cnt;
isn[u] = 1;
s.push(u);
for (int i: vec[u])
{
if (!dfn[i])
{
Tarjan(i);
low[u] = min(low[u],low[i]);
}
else if (isn[i])
low[u] = min(low[u],dfn[i]);
}
if (dfn[u] == low[u])
{
int x;
col++;
do
{
x = s.top();
s.pop();
isn[x] = 0;
id[x] = col;
} while (x != u);
}
}
queue<int>q;
void toposort()
{
while (!q.empty())
{
int now = q.front();
q.pop();
bool t = 0;
if (ans[now] && p[now] > sz[now]) ans[now] = -1;
for (int i: tec[now])
{
in[i]--;
if (!in[i]) q.push(i);
if (ans[i] == -1 || !ans[now]) continue;
if (ans[now] == -1 || p[now] >= sz[now]) ans[i] = -1;
else ans[i] = (ans[i]+ans[now])%M+M;
}
}
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin >> t;
for (int k = 1; k <= t; k++)
{
cin >> n;
for (int i = 1; i <= n; i++)
vec[i].clear(),tec[i].clear(),dfn[i] = low[i] = ans[i] = p[i] = sz[i] = in[i] = isn[i] = 0;
cnt = col = 0;
for (int i = 1; i <= n; i++)
cin >> a[i] >> b[i],
vec[i].push_back(a[i]),vec[i].push_back(b[i]);
for (int i = 1; i <= n; i++)
if (!dfn[i])
Tarjan(i);
for (int i = 1; i <= n; i++)
{
sz[id[i]]++;
if (id[a[i]] == id[i]) p[id[i]]++;
else tec[id[i]].push_back(id[a[i]]),in[id[a[i]]]++;
if (id[b[i]] == id[i]) p[id[i]]++;
else tec[id[i]].push_back(id[b[i]]),in[id[b[i]]]++;
}
for (int i = 1; i <= n; i++)
cin >> c[i],ans[id[i]] += c[i];
for (int i = 1; i <= col; i++)
if (!in[i]) q.push(i);
toposort();
if (ans[id[1]] == -1) cout << "Case #" << k << ": UNBOUNDED\n";
else cout << "Case #" << k << ": " << ans[id[1]]%M << '\n';
}
return 0;
}
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...