专栏文章

高等数学初步

xxujindong_
个人记录参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@min5p20f
此快照首次捕获于
2025/12/01 20:59
3 个月前
此快照最后确认于
2025/12/01 20:59
3 个月前
查看原文

极限

我们先来定义数列的极限。感性理解，极限是指这个数列越往后，值会越靠近某个值 aa，且这个靠近可以无限接近，我们将其描述为对于任意一个距离 ε\varepsilon 都可以比它更小，且在某个点之后都满足距离比 ε\varepsilon 小。因此可以定义：
数列的极限：设 xnx_n 为一数列，如果存在常数 aa 使得对于任意正数 ε\varepsilon，总存在正整数 NN 使得当 n>Nn>N，∣xn−a∣<ε|x_n-a|<\varepsilon，称数列 xnx_n 收敛于 aa，记作 lim⁡n→∞xn=a\lim_{n\to\infty}x_n=a。若不存在，称数列 xnx_n 发散。
类似地，我们可以定义函数的极限。先定义趋于有限值的极限，这要求函数在不断接近一个 x0x_0 处时，值能无限接近极限：
自变量趋于有限值时函数的极限：若存在常数 AA 使得对于任意正数 ε\varepsilon，总存在正数 δ\delta，使得当 0<∣x−x0∣<δ0<|x-x_0|<\delta，满足 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon，那么称常数 AA 是函数 f(x)f(x) 当 x→x0x\to x_0 时的极限，记作 lim⁡x→x0f(x)=A\lim_{x\to x_0}f(x)=A。
注意，函数在 x0x_0 处可以未定义，只需要在周围有定义，或者说是某个去心邻域。邻域 U(x0,δ)(x0∈R,δ>0)U(x_0,\delta)(x_0\in\mathbb R,\delta>0) 为开区间 (x0−δ,x0+δ)(x_0-\delta,x_0+\delta)，去心邻域 U˚(x0,δ)(x0∈R,δ>0)\mathring U(x_0,\delta)(x_0\in\mathbb R,\delta>0) 为 (x0−δ,x0+δ)∖{x0}(x_0-\delta,x_0+\delta)\setminus\{x_0\}。
我们也可以定义左极限和右极限，只从左侧接近或只从右侧接近，将 0<∣x−x0∣<δ0<|x-x_0|<\delta 改为 x0−δ<x<x0x_0-\delta<x<x_0 或 x0<x<x0+δx_0<x<x_0+\delta，分别记作 lim⁡x→x0−f(x)=A,lim⁡x→x0+f(x)=A\lim_{x\to x_0^-}f(x)=A,\lim_{x\to x_0^+}f(x)=A。极限就是要求左极限和右极限都存在且相等。
我们也可以让函数往两边接近无穷。将 0<∣x−x0∣<δ0<|x-x_0|<\delta 改为 ∣x∣>X|x|>X，其中 XX 是某个正数，就得到 lim⁡x→∞f(x)\lim_{x\to\infty}f(x) 的定义。同理可以定义 lim⁡x→+∞f(x),lim⁡x→−∞f(x)\lim_{x\to+\infty}f(x),\lim_{x\to-\infty}f(x)，改为 x>Xx>X 或 x<Xx<X 即可。
用极限，我们也可以描述函数趋向于无穷大，将 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon 改为 ∣f(x)∣>M|f(x)|>M，其中 MM 是任意正数。按上面的定义，f(x)f(x) 在 x→x0/∞x\to x_0/\infty 时没有极限，但我们仍然称极限是无穷大。此时我们也称 f(x)f(x) 是 x→x0/∞x\to x_0/\infty 时的无穷大。
对应的，我们已经定义了无穷小，也就是 f(x)f(x) 在 x→x0/∞x\to x_0/\infty 时极限为 00，称 f(x)f(x) 是 x→x0/∞x\to x_0/\infty 时的无穷小。显然在同一变化过程中，无穷大的倒数是无穷小，无穷小（不为 00）的倒数是无穷大。
极限有以下运算法则，以下性质是显然的：
  • 两个无穷小的和是无穷小；
  • 有界函数与无穷小的乘积是无穷小；
  • lim⁡(f(x)±g(x))=lim⁡f(x)±lim⁡g(x)\lim(f(x)\pm g(x))=\lim f(x)\pm\lim g(x)；
  • lim⁡f(x)g(x)=lim⁡f(x)⋅lim⁡g(x)\lim f(x)g(x)=\lim f(x)\cdot\lim g(x)；
  • lim⁡f(x)g(x)=lim⁡f(x)lim⁡g(x)(lim⁡g(x)≠0)\lim \frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}(\lim g(x)\ne0)。
对数列的极限类似。
对函数的复合，也可以找到规律：若 (f∘g)(x)(f\circ g)(x) 在 x0x_0 的某去心邻域有定义， lim⁡x→x0/∞g(x)=u0/∞,lim⁡u→u0/∞f(u)=A\lim_{x\to x_0/\infty}g(x)=u_0/\infty,\lim_{u\to u_0/\infty}f(u)=A，且存在 x0x_0 的某去心邻域的 g(x)g(x) 都不等于 u0u_0，则 lim⁡x→x0/∞(f∘g)(x)=A\lim_{x\to x_0/\infty}(f\circ g)(x)=A。这说的其实就是将 g(x)g(x) 放到自变量上，也是一个向 u0u_0 的逼近。后面的一句特判是防止 xx 周围形成一个平台，比如 f(x)=[x=1],g(x)=1f(x)=[x=1],g(x)=1，这样 g(x)g(x) 无法在 x0x_0 周围形成一个向 u0u_0 的逼近，因为取到 u0u_0。
下面讲述极限存在的一些准则：
夹逼准则：若在 x0x_0 的某去心邻域内或 ∣x∣>M|x|>M 时 g(x)≤f(x)≤h(x)g(x)\leq f(x)\leq h(x)，且 lim⁡x→x0/∞g(x)=lim⁡x→x0/∞h(x)=A\lim_{x\to x_0/\infty}g(x)=\lim_{x\to x_0/\infty}h(x)=A，则 lim⁡x→x0/∞f(x)=A\lim_{x\to x_0/\infty}f(x)=A。
容易感性理解。对数列类似。
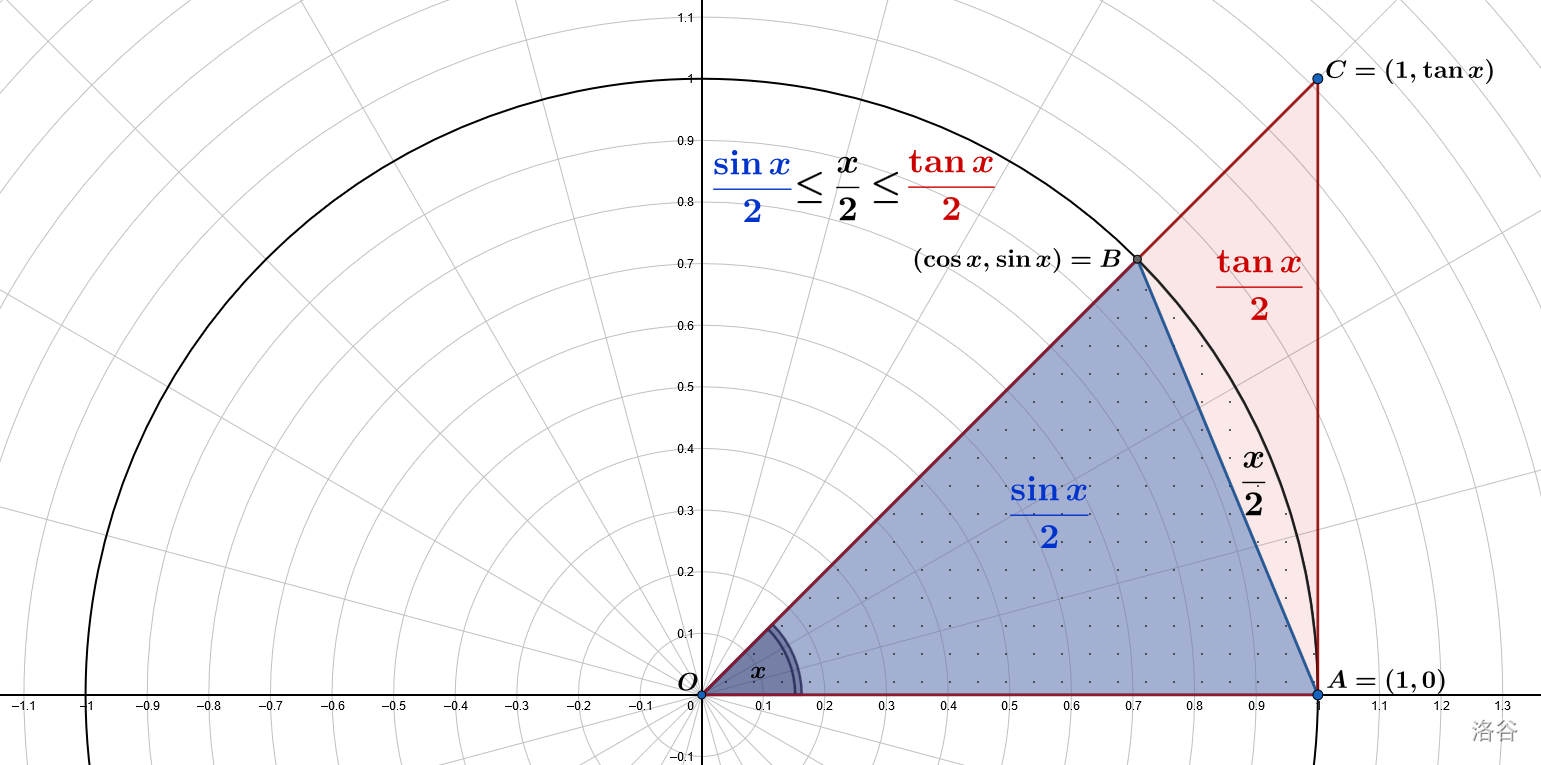
一个经典例子是 lim⁡x→0sin⁡xx=1\lim_{x\to0}\frac{\sin x}x=1。如下图，我们有一个单位元和一个圆心角 ∠AOC=x(0<x<π2)\angle AOC=x(0<x<\frac\pi2)，有 S△AOB<S扇形AOB<S△AOCS_{\triangle AOB}<S_{\text{扇形}AOB}<S_{\triangle AOC}，即 sin⁡x2<x2<tan⁡x2,cos⁡x<sin⁡xx<1\frac{\sin x}2<\frac x2<\frac{\tan x}2,\cos x<\frac{\sin x}x<1，而前后两者在 x→0x\to0 的极限都是 11。
单调有界定理：单调有界数列必有极限。对于函数，若 f(x)f(x) 在 x0x_0 的某个左邻域内单调且有界，则 f(x)f(x) 在 x0x_0 的左极限存在。
感性理解，单调要求往一个方向，但是有界又要求不能超过 ±M\pm M，所以只能无限接近某个位置而不越过。
经典例子是 lim⁡x→∞(1+1x)x=e\lim_{x\to\infty}(1+\frac1x)^x=e。我们先构造 an=(1+1n)na_n=(1+\frac1n)^n，证明它的极限存在。
首先它单调递增，因为 an=∑i=0nCni1ni=∑i=0n1i!∏j=0i(1−jn)a_n=\sum_{i=0}^nC_n^i\frac1{n^i}=\sum_{i=0}^n\frac1{i!}\prod_{j=0}^i(1-\frac jn)，每一项都是单调递增的。而且它有界，将其放缩为 ∑i=0n1i!≤1+∑i=0n12i<3\sum_{i=0}^n\frac1{i!}\leq1+\sum_{i=0}^n\frac1{2^i}<3。因此它有极限。对原问题，构造 g(x)=(1+1⌊x⌋+1)⌊x⌋,h(x)=(1+1⌊x⌋)⌊x⌋+1g(x)=(1+\frac1{\lfloor x\rfloor+1})^{\lfloor x\rfloor},h(x)=(1+\frac1{\lfloor x\rfloor})^{\lfloor x\rfloor+1}，极限都是 ee，用夹逼准则即可。
柯西极限存在准则：数列 xnx_n 收敛的充要条件是对于任意正数 ε\varepsilon，存在正整数 NN 使 ∀n,m>N,∣xn−xm∣<ε\forall n,m>N,|x_n-x_m|<\varepsilon。
必要性显然，设极限是 aa，存在 NN 使 ∀n>N,∣xn−a∣<ε2\forall n>N,|x_n-a|<\frac\varepsilon2。
感性理解充分性，考虑在 NN 之后，所有 xnx_n 会落在一个长度小于 ε\varepsilon 的区间内，且随着 ε\varepsilon 的缩小，区间长度也缩小，且趋向 00。因此最后区间内会剩一个单点。上述过程也相当于归约到了闭区间套定理。
对于极限，我们可以定义无穷小之间的比较。
在同一个变化过程中，若 lim⁡βα=0\lim\frac\beta\alpha=0，称 β\beta 是比 α\alpha 高阶的无穷小，记作 β=o(α)\beta=o(\alpha)；
若 lim⁡βα=∞\lim\frac\beta\alpha=\infty，称 β\beta 是比 α\alpha 低阶的无穷小；
若 lim⁡βα=c≠0\lim\frac\beta\alpha=c\ne0，称 β\beta 与 α\alpha 是同阶无穷小。特别地，若 c=1c=1，称 β\beta 与 α\alpha 是等价无穷小，记作 β∼α\beta\sim\alpha；
若 lim⁡βαk=c≠0\lim\frac\beta{\alpha^k}=c\ne0，称 β\beta 是关于 α\alpha 的 kk 阶无穷小。
关于等价无穷小有以下定理：
β\beta 与 α\alpha 是等价无穷小的充要条件是 β=α+o(α)\beta=\alpha+o(\alpha)。
必要性：lim⁡β−αα=lim⁡(βα−1)=0,β−α=o(α)\lim\frac{\beta-\alpha}\alpha=\lim(\frac\beta\alpha-1)=0,\beta-\alpha=o(\alpha)。
充分性：lim⁡βα=lim⁡α+o(α)α=lim⁡(1+o(α)α)=1\lim\frac\beta\alpha=\lim\frac{\alpha+o(\alpha)}\alpha=\lim(1+\frac{o(\alpha)}\alpha)=1。
若 α∼α~,β∼β~\alpha\sim\tilde\alpha,\beta\sim\tilde\beta，且 lim⁡α~β~\lim\frac{\tilde\alpha}{\tilde\beta} 存在，则 lim⁡αβ=lim⁡α~β~\lim\frac\alpha\beta=\lim\frac{\tilde\alpha}{\tilde\beta}。
证明：lim⁡αβ=lim⁡α~β~ββ~α~α=lim⁡α~β~lim⁡ββ~lim⁡α~α=lim⁡α~β~\lim\frac\alpha\beta=\lim\frac{\tilde\alpha}{\tilde\beta}\frac\beta{\tilde\beta}\frac{\tilde\alpha}\alpha=\lim\frac{\tilde\alpha}{\tilde\beta}\lim\frac\beta{\tilde\beta}\lim\frac{\tilde\alpha}\alpha=\lim\frac{\tilde\alpha}{\tilde\beta}。
通过极限，我们可以刻画函数的连续性，就是两端能向这里的函数值逼近，不能出现断层，即若函数 y=f(x)y=f(x) 在点 x0x_0 的某一邻域有定义且 lim⁡x→x0f(x)=f(x0)\lim_{x\to x_0}f(x)=f(x_0)，称函数 y=f(x)y=f(x) 在点 x0x_0 连续。同理可定义左连续和右连续。也可定义在一个区间连续，就是在内部的某个点连续，如果含左端点就在左端点左连续，含右端点就在右端点右连续。
根据极限的四则运算，可以立即得出两个在 x0x_0 连续的函数的和/差/积/分母不为 00 的商在 x0x_0 连续。
讨论反函数的连续性，易得：若函数 y=f(x)y=f(x) 在区间 IxI_x 单调递增/单调递减且连续，则它的反函数 x=f−1(y)x=f^{-1}(y) 在区间 Iy={y∣y=f(x),x∈Ix}I_y=\{y\mid y=f(x),x\in I_x\} 单调递增/单调递减且连续。直觉上容易理解，这相当于交换 xx 轴和 yy 轴。
对复合函数，用复合函数的极限可得：若 (f∘g)(x)(f\circ g)(x) 在 x0x_0 的某去心邻域有定义， u=g(x)u=g(x) 在 x0x_0 连续且 g(x0)=u0g(x_0)=u_0，y=f(u)y=f(u) 在 u0u_0 连续，则 (f∘g)(x)(f\circ g)(x) 在 x0x_0 连续。
综上，我们可以证明初等函数（幂函数、指数函数、对数函数、三角函数、反三角函数）在其定义域内都连续。
关于函数的连续性，有以下几个定理：
有界性与最大值最小值定理：在闭区间上的函数在该区间上有界，且一定能取得它的最大值和最小值。
容易感性理解。这里闭区间是必要的，开区间有可能在端点处左/右极限为无穷大，如 tan⁡x\tan x 在 (−π2,π2)(-\frac\pi2,\frac\pi2)。
介值定理：设函数 f(x)f(x) 在 [a,b][a,b] 连续，且 f(a)=A,f(b)=Bf(a)=A,f(b)=B，则对于任意的 min⁡(A,B)<C<max⁡(A,B)\min(A,B)<C<\max(A,B)，存在 a<ξ<b,f(ξ)=Ca<\xi<b,f(\xi)=C。
几何意义就是函数值从 AA 连续变化到 BB，必然经过中间每个值。

导数与微分

导数描述了一个函数在某点的瞬时增长率，或者说切线斜率。其定义为 f′(x0)=lim⁡h→0f(x0+h)−f(x0)hf'(x_0)=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)}h。若这个极限存在，称函数 y=f(x)y=f(x) 在 x0x_0 处可导。连续是可导的充分条件（不是必要条件，比如考虑 ∣x∣|x| 在 x0=0x_0=0）。以下是几个常用导数：
(C)′=0(C)'=0 (xn)′(n∈N∗)=lim⁡h→0(x+h)n−xnh=lim⁡h→0∑i=0n−1Cnixihn−i−1=nxn−1\begin{aligned}&(x^n)'(n\in\mathbb N^\ast)\\&=\lim_{h\to 0}\frac{(x+h)^n-x^n}h\\&=\lim_{h\to0}\sum_{i=0}^{n-1}C_n^ix^ih^{n-i-1}\\&=nx^{n-1}\end{aligned} (xμ)′(μ∈R,x0≠0)=lim⁡h→0(x+h)μ−xμh=lim⁡h→0xμ−1(1+hx)μ−1hx=lim⁡h→0xμ−1(1+x)μ−1x=lim⁡h→0xμ−1(1+x)μ−1ln⁡(1+x)μμln⁡(1+x)x=xμ−1lim⁡t→0tln⁡(t+1)lim⁡x→0μln⁡(1+x)x(t=(1+x)μ−1)=xμ−1μ\begin{aligned}&(x^\mu)'(\mu\in\mathbb R,x_0\ne0)\\&=\lim_{h\to0}\frac{(x+h)^\mu-x^\mu}h\\&=\lim_{h\to0}x^{\mu-1}\frac{(1+\frac hx)^\mu-1}{\frac hx}\\&=\lim_{h\to0}x^{\mu-1}\frac{(1+x)^\mu-1}x\\&=\lim_{h\to0}x^{\mu-1}\frac{(1+x)^\mu-1}{\ln(1+x)^\mu}\frac{\mu\ln(1+x)}x\\&=x^{\mu-1}\lim_{t\to0}\frac t{\ln(t+1)}\lim_{x\to0}\frac{\mu\ln(1+x)}x(t=(1+x)^\mu-1)\\&=x^{\mu-1}\mu\end{aligned} (sin⁡x)′=lim⁡h→0sin⁡(x+h)−sin⁡xh=lim⁡h→02cos⁡(x+h2)sin⁡h2h=lim⁡h→0cos⁡(x+h2)lim⁡h→0sin⁡h2h2=cos⁡x\begin{aligned}&(\sin x)'\\&=\lim_{h\to0}\frac{\sin(x+h)-\sin x}h\\&=\lim_{h\to0}\frac{2\cos(x+\frac h2)\sin\frac h2}h\\&=\lim_{h\to0}\cos(x+\frac h2)\lim_{h\to0}\frac{\sin\frac h2}{\frac h2}\\&=\cos x\end{aligned} (cos⁡x)′=lim⁡h→0cos⁡(x+h)−cos⁡hh=lim⁡h→0−2sin⁡(x+h2)sin⁡h2h=lim⁡h→0−sin⁡(x+h2)lim⁡h→0sin⁡h2h2=−sin⁡x\begin{aligned}&(\cos x)'\\&=\lim_{h\to0}\frac{\cos(x+h)-\cos h}h\\&=\lim_{h\to0}\frac{-2\sin(x+\frac h2)\sin\frac h2}h\\&=\lim_{h\to0}-\sin(x+\frac h2)\lim_{h\to0}\frac{\sin\frac h2}{\frac h2}\\&=-\sin x\end{aligned} (ax)′(a>0,a≠1)=lim⁡h→0ax+h−axh=axlim⁡h→0ah−1h=axlim⁡t→0tlog⁡a(1+t)(t=ah−1)=axlim⁡t→01log⁡a(1+t)1t=axlog⁡ae=axln⁡a\begin{aligned}&(a^x)'(a>0,a\ne1)\\&=\lim_{h\to0}\frac{a^{x+h}-a^x}h\\&=a^x\lim_{h\to0}\frac{a^h-1}h\\&=a^x\lim_{t\to0}\frac t{\log_a(1+t)}(t=a^h-1)\\&=a^x\lim_{t\to0}\frac1{\log_a(1+t)^{\frac1t}}\\&=\frac{a^x}{\log_ae}\\&=a^x\ln a\end{aligned} (ex)′=ex(e^x)'=e^x (log⁡ax)′(a>0,a≠1)=lim⁡h→0log⁡a(x+h)−log⁡axh=lim⁡h→0log⁡ax+hxh=1xlim⁡h→0log⁡a(1+hx)hx=1xlog⁡ae=1xln⁡a\begin{aligned}&(\log_a x)'(a>0,a\ne1)\\&=\lim_{h\to0}\frac{\log_a(x+h)-\log_ax}h\\&=\lim_{h\to0}\frac{\log_a\frac{x+h}x}h\\&=\frac1x\lim_{h\to0}\frac{\log_a(1+\frac hx)}{\frac hx}\\&=\frac1x\log_ae\\&=\frac1{x\ln a}\end{aligned} (ln⁡x)′=1x(\ln x)'=\frac1x
函数有以下求导法则：
  • (u±v)′=u′±v′(u\pm v)'=u'\pm v'；
  • (uv)′=u′v+uv′(uv)'=u'v+uv'；
证明：(u(x)v(x))′=lim⁡h→0u(x+h)v(x+h)−u(x)v(x)h=lim⁡h→0v(x+h)(u(x+h)−u(x))+u(x)(v(x+h)−v(x))h=lim⁡h→0v(x+h)lim⁡h→0u(x+h)−u(x)h+lim⁡h→0u(x)(v(x+h)−v(x))h=u′(x)v(x)+v′(x)u(x)\begin{aligned}&(u(x)v(x))'\\&=\lim_{h\to0}\frac{u(x+h)v(x+h)-u(x)v(x)}h\\&=\lim_{h\to0}\frac{v(x+h)(u(x+h)-u(x))+u(x)(v(x+h)-v(x))}h\\&=\lim_{h\to0}v(x+h)\lim_{h\to0}\frac{u(x+h)-u(x)}h+\lim_{h\to0}\frac{u(x)(v(x+h)-v(x))}h\\&=u'(x)v(x)+v'(x)u(x)\end{aligned}
  • (uv)′=u′v−uv′v2(\frac uv)'=\frac{u'v-uv'}{v^2}；
证明：(u(x)v(x))′=lim⁡h→0u(x+h)v(x+h)−u(x)v(x)h=lim⁡h→0u(x+h)v(x)−u(x)v(x+h)v(x+h)v(x)h=lim⁡h→0v(x)(u(x+h)−u(x))−u(x)(v(x+h)−v(x))v(x+h)v(x)h=u′(x)v(x)+u(x)v′(x)v(x)2\begin{aligned}&\left(\frac{u(x)}{v(x)}\right)'\\&=\lim_{h\to0}\frac{\frac{u(x+h)}{v(x+h)}-\frac{u(x)}{v(x)}}h\\&=\lim_{h\to0}\frac{u(x+h)v(x)-u(x)v(x+h)}{v(x+h)v(x)h}\\&=\lim_{h\to0}\frac{v(x)(u(x+h)-u(x))-u(x)(v(x+h)-v(x))}{v(x+h)v(x)h}\\&=\frac{u'(x)v(x)+u(x)v'(x)}{v(x)^2}\end{aligned}
对反函数，有：若函数 y=f(x)y=f(x) 在区间 IxI_x 单调、可导且 f′(x)≠0f'(x)\ne0，那么它的反函数 x=f−1(y)x=f^{-1}(y) 在区间 Iy={y∣y=f(x),x∈Ix}I_y=\{y\mid y=f(x),x\in I_x\} 内可导且 f−1(x)′=1f′(y)f^{-1}(x)'=\frac1{f'(y)}。同理，反函数可以看成交换 xx 轴和 yy 轴。
对复合函数，有：若 u=g(x)u=g(x) 在点 xx 处可导且 y=f(u)y=f(u) 在点 u=g(x)u=g(x) 处可导，那么 y=(f∘g)(x)y=(f\circ g)(x) 在点 xx 处可导且 (f∘g)(x)=f′(u)g′(x)(f\circ g)(x)=f'(u)g'(x)。这也是好理解的，xx 输入 gg 后在 uu 周围产生了变化速度为 g′(x)g'(x) 的点列，套一层 ff 后变成了 f′(u)g′(x)f'(u)g'(x)。
导数可以嵌套，我们定义高阶导数 f(n)(x)f^{(n)}(x) 为导数迭代 nn 次。
对于一个函数，如果它在点 xx 处可导，我们就可以用切线拟合函数的曲线，这就是说，用 f′(x)Δxf'(x)\Delta x 估计 Δy\Delta y。
此时有 lim⁡Δx→0ΔyΔx=f′(x0)\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}=f'(x_0)，则 ΔyΔx=f′(x0)+α(lim⁡Δx→0α=0)\frac{\Delta y}{\Delta x}=f'(x_0)+\alpha(\lim_{\Delta x\to0}\alpha=0)，移项可得 Δy=f′(x0)Δx+αΔx=Δy=f′(x0)Δx+o(Δx)\Delta y=f'(x_0)\Delta x+\alpha\Delta x=\Delta y=f'(x_0)\Delta x+o(\Delta x)。这也是微分的定义：
设函数 y=f(x)y=f(x) 在某区间内有定义，x0,x0+Δxx_0,x_0+\Delta x 在这个区间内，若函数的增量 Δy=f(x0+Δx)−f(x0)\Delta y=f(x_0+\Delta x)-f(x_0) 可表示为 Δy+AΔx+o(Δx)\Delta y+A\Delta x+o(\Delta x)，其中 AA 是与 Δx\Delta x 无关的常数，那么称函数 y=f(x)y=f(x) 在 x0x_0 处可微，AΔxA\Delta x 是函数 y=f(x)y=f(x) 在点 x0x_0 相应于自变量增量 xx 的微分，记作 dy\mathrm dy。可导是可微的充要条件，且一定满足 A=f′(x0)A=f'(x_0)。这也说明导数是函数的微分除以自变量的微分，即 dydx\frac{\mathrm dy}{\mathrm dx}。
根据导数的运算，容易推出微分的运算。
下面介绍微分的几个中值定理：
先引入费马引理：设函数 f(x)f(x) 在点 x0x_0 的某邻域 U(x0)U(x_0) 有定义且在 x0x_0 处可导，若 x0x_0 是 f(x)f(x) 在 U(x0)U(x_0) 的最大值或最小值，则 f′(x0)=0f'(x_0)=0。
这就是说，在这个函数的局部极值，切线是水平线。证明考虑左极限和右极限一个 ≥0\geq0 一个 ≤0\leq0。称导数为 00 的点为函数的驻点。
罗尔定理：若函数 f(x)f(x) 在 [a,b][a,b] 上连续且在 (a,b)(a,b) 内可导，且 f(a)=f(b)f(a)=f(b)，则存在 a<ξ<ba<\xi<b 使 f′(ξ)=0f'(\xi)=0。
取不是端点的最大/最小值，用费马引理即可。
我们可以拓展到 f(a)≠f(b)f(a)\ne f(b) 的情况，得到拉格朗日中值定理：若函数 f(x)f(x) 在 [a,b][a,b] 上连续且在 (a,b)(a,b) 内可导，则存在 a<ξ<ba<\xi<b 使 f′(ξ)=f(a)−f(b)a−bf'(\xi)=\frac{f(a)-f(b)}{a-b}。
证明将函数偏移，减掉直线 ABAB，对 g(x)=f(x)−xf(a)−f(b)a−bg(x)=f(x)-x\frac{f(a)-f(b)}{a-b} 使用罗尔定理即可。实际意义是在 (a,b)(a,b) 内能找到一点的切线平行于直线 ABAB。
将这个式子变形，得到 Δy=f′(x+θΔx)⋅Δx\Delta y=f'(x+\theta\Delta x)\cdot\Delta x，其中 θ\theta 是某个 0<θ<10<\theta<1 的值。这也被称为有限增量定理。
这可以导出，若函数 f(x)f(x) 在 [a,b][a,b] 上连续且在 (a,b)(a,b) 内可导且导数恒为 00，那么 f(x)f(x) 在区间 [a,b][a,b] 是常数。任取 a≤x1<x2≤ba\leq x_1<x_2\leq b，都存在 f′(ξ)=f(x1)−f(x2)x1−x2=0,f(x1)=f(x2)f'(\xi)=\frac{f(x_1)-f(x_2)}{x_1-x_2}=0,f(x_1)=f(x_2)。
我们还可以把 a−ba-b 换成另一个函数，得到柯西中值定理： 若函数 f(x),F(x)f(x),F(x) 在 [a,b][a,b] 上连续且在 (a,b)(a,b) 内可导，且 F′(x)≠0(a<x<b)F'(x)\ne0(a<x<b)，则存在 a<ξ<ba<\xi<b 使 f′(ξ)F′(ξ)=f(a)−f(b)F(a)−F(b)\frac{f'(\xi)}{F'(\xi)}=\frac{f(a)-f(b)}{F(a)-F(b)}。
感性理解，这相当于把自变量换成一个 F(x)F(x)，可以前后移动，变成了一条曲线。构造 g(x)=f(x)−f(a)−f(b)F(a)−F(b)F(x)g(x)=f(x)-\frac{f(a)-f(b)}{F(a)-F(b)}F(x) 用罗尔定理即可。
通过柯西中值定理，可以导出一种求 00\frac00 型极限的方式。
洛必达法则：若 lim⁡x→a/∞f(x)=lim⁡x→a/∞F(x)=0\lim_{x\to a/\infty}f(x)=\lim_{x\to a/\infty}F(x)=0，在点 a/∞a/\infty 的某去心邻域内 f′(x),F′(x)f'(x),F'(x) 存在且 F′(x)≠0F'(x)\ne0 且 lim⁡x→a/∞f′(x)F′(x)\lim_{x\to a/\infty}\frac{f'(x)}{F'(x)} 存在或为无穷大，则 lim⁡x→a/∞f(x)F(x)=lim⁡x→a/∞f′(x)F′(x)\lim_{x\to a/\infty}\frac{f(x)}{F(x)}=\lim_{x\to a/\infty}\frac{f'(x)}{F'(x)}。
证明：我们钦定 f(a)=F(a)=0f(a)=F(a)=0，当 xx 从 aa 左侧/右侧逼近时，我们可以将 f(x)F(x)\frac{f(x)}{F(x)} 替换为 f′(ξ)F′(ξ)\frac{f'(\xi)}{F'(\xi)}，这个 ξ\xi 在 x,ax,a 中间向 aa 逼近。
用导数可以在某个点 x0x_0 拟合函数。考虑用更高阶多项式去拟合，我们尝试构造一个多项式 pn(x−x0)=∑i=0nai(x−x0)ip_n(x-x_0)=\sum_{i=0}^na_i(x-x_0)^i 使得 pnp_n 的 0∼n0\sim n 阶导在 x0x_0 处和 ff 的 0∼n0\sim n 阶导相等。导 ii 次后，低于 ii 的项都没了，高于 ii 的项有个 x−x0x-x_0 也为 00，第 ii 项变成 i!aii!a_i，则 ai=f(i)(x0)i!a_i=\frac{f^{(i)}(x_0)}{i!}。下面我们研究误差，设 f(x)=Rn(x)+∑i=0nf(i)i!(x−x0)if(x)=R_n(x)+\sum_{i=0}^n\frac{f^{(i)}}{i!}(x-x_0)^i。
根据上面有 Rn(k)(x)=0(0≤k≤n)R_n^{(k)}(x)=0(0\leq k\leq n)。对 lim⁡x→x0Rn(x)(x−x0)n\lim_{x\to x_0}\frac{R_n(x)}{(x-x_0)^n}，我们可以洛必达 nn 次，上面是 00，下面是 n!n!。因此 Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n)。
假设 f(x)f(x) 在 x0x_0 的某邻域内有 n+1n+1 阶导数，我们还可以用中值定理继续分析。此时有 Rn(k)(x)=0(0≤k≤n),Rn(n+1)(x)=f(n+1)(x)R_n^{(k)}(x)=0(0\leq k\leq n),R_n^{(n+1)}(x)=f^{(n+1)}(x)。对 Rn(x)(x−x0)n+1\frac{R_n(x)}{(x-x_0)^{n+1}}，在 [x0,x][x_0,x] 用柯西中值定理，找到 Rn′(ξ1)n(ξ1−x0)n=Rn(x)(x−x0)n+1\frac{R_n'(\xi_1)}{n(\xi_1-x_0)^{n}}=\frac{R_n(x)}{(x-x_0)^{n+1}}。我们对 Rn′(ξ1)n(ξ1−x0)n\frac{R_n'(\xi_1)}{n(\xi_1-x_0)^{n}} 在 [x0,ξ1][x_0,\xi_1] 再用一次柯西中值定理找到 ξ2\xi_2。用 n+1n+1 次，会得到一个 x0<ξ<xx_0<\xi<x 满足 Rn(x)(x−x0)n+1=Rn(n+1))(ξ)(n+1)!\frac{R_n(x)}{(x-x_0)^{n+1}}=\frac{R_n^{(n+1)})(\xi)}{(n+1)!}，则 Rn(x)=Rn(n+1))(ξ)(n+1)!(x−x0)n+1R_n(x)=\frac{R_n^{(n+1)})(\xi)}{(n+1)!}(x-x_0)^{n+1}。

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...