专栏文章

赛前模拟1-20250825(总结)

___H_J_M__
个人记录参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mio51ook
此快照首次捕获于
2025/12/02 13:29
3 个月前
此快照最后确认于
2025/12/02 13:29
3 个月前
查看原文

Part 1 赛时

T1

首先我们可以发现测试点分为两类：
  • n=m+1n=m+1 ，这只是一个普通的树，我们可以对每一个节点的子节点，按编号排序，进行贪心，时间复杂度O(N logN)O(N\ logN)，Accepted\color{green} Accepted
  • n=mn=m ，很明显，这是一个基环树，当时我已经想到了可以挨个断边，但当时我认为这太暴力了！，于是写了一个神奇的贪心，喜提64tps\color {red} 64tps

T2

看看这数据规模与约定：
测试点编号nnmmai=1a_i=1bi=ai+1b_i=a_i+1分支不超过 33
11≤5\le 5=1=1否否是
22≤10\le 10≤n−1\le n-1否是是
33≤15\le 15≤n−1\le n-1是否否
44≤103\le 10^3=1=1否否是
55≤3×104\le 3\times 10^4=1=1是否否
66≤3×104\le 3\times 10^4=1=1否否否
77≤3×104\le 3\times 10^4≤n−1\le n-1是否否
88≤5×104\le 5\times 10^4≤n−1\le n-1是否否
99≤103\le 10^3≤n−1\le n-1否是是
1010≤3×104\le 3\times 10^4≤n−1\le n-1否是是
1111≤5×104\le 5\times 10^4≤n−1\le n-1否是是
1212≤50\le 50≤n−1\le n-1否否是
1313≤50\le 50≤n−1\le n-1否否是
1414≤200\le 200≤n−1\le n-1否否是
1515≤200\le 200≤n−1\le n-1否否是
1616≤103\le 10^3≤n−1\le n-1否否是
1717≤103\le 10^3≤n−1\le n-1否否否
1818≤3×104\le 3\times 10^4≤n−1\le n-1否否否
1919≤3×104\le 3\times 10^4≤n−1\le n-1否否否
2020≤5×104\le 5\times 10^4≤n−1\le n-1否否否
简单的数了一下，如果把所有特殊点加上，可以拿到80tps\color {green} 80tps，太值了，于是我完成了(3/4) -> 前三个，于是，我们来一个一个分析：
  1. m=1，这个十分明显，m=1代表只用出现一条赛道，如果要让这条赛道的长度最长，这条赛道其实就是这个树的直径，十分简单
  2. ai=1，这是一个菊花图：
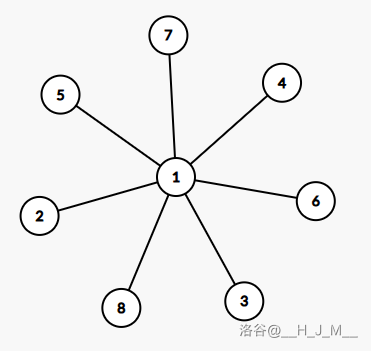
对于这种情况，我们发现每一条赛道至多为2条边，如果m∗2≤nm*2\le n，很明显我们直接曲最大的2∗m2*m个，一大一小进行匹配，但是如果m∗2>nm*2>n呢，我们可以加入若干条连接1的边，且其边为0，补全至第一种。
  1. ai=bi+1这是一条链，我们可以使用二分，每一次依次加边，直到>=mid,看能不能全部分配够。

T3

我在考场上，看到了这个：
测试点编号type\text{type}n=m=n = m=
1,21,2A31010
3,43,4C31010
5,65,6A3100100
77C3100100
8,98,9A32×1032\times 10^3
10,1110,11C32×1032\times 10^3
12,1312,13A110510^5
14,15,1614, 15, 16A210510^5
1717A310510^5
18,1918,19B110510^5
20,2120,21C110510^5
2222C210510^5
23,24,2523, 24, 25C310510^5
于是我先写了所有A的骗分，但时间复杂度算错了，只拿了24tps\color {red} 24tps

T4

暴力
20tps\color {red} 20tps

Part 2 赛后

T1

赛后我很快发现暴力断边的时间复杂度 5000∗50005000*5000 完全可以啊,于是就Accepted\color{green} Accepted。

T2

肉眼可得: 我们可以使用二分答案，check的内容为长度大于等于mid是否能超过m个。
这道题我们可以发现每一个赛道可以分解为两条链，我们记录一下沿着每一个当前节点的子节点向下的最长链，为了满足要求，我们应当选择两条链使其最接近mid，如果剩下一些链没写，传上去。
（当然，如果一条链就大于mid了，便直接ans++）
这一段可以使用set实现，但我用的是数组。
CPP
for(int i=1;i<cnt;i++){
    if(vis[i]) continue;
    int it=lower_bound(a+i+1,a+cnt+1,mid-a[i])-a;
		if(it==cnt+1) continue;
		while(vis[it]&&it<cnt) it++;
		if(!vis[it]&&a[i]+a[it]>=mid)
			ans++,vis[i]=vis[it]=1;
	}
code:
CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=5e4+5;
int n,m;
int ans,mid;
int a[N],b[N],vis[N];
int tot,head[N],ver[N<<1],nxt[N<<1],edg[N<<1];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b,int c){
	ver[++tot]=b,edg[tot]=c;
	nxt[tot]=head[a],head[a]=tot;
}
void dfs(int x,int fa){
	for(int i=head[x];i;i=nxt[i]){
		int y=ver[i];
		if(y==fa) continue;
		dfs(y,x);
	}
	int cnt=0;
	for(int i=head[x];i;i=nxt[i]){
		int y=ver[i],w=edg[i];
		if(y==fa) continue;
		if(b[y]+w>=mid) ans++;
		else a[++cnt]=b[y]+w;
	}
	sort(a+1,a+cnt+1);
	for(int i=1;i<=cnt;i++)
		vis[i]=0;
	for(int i=1;i<cnt;i++){
		if(vis[i]) continue;
		int it=lower_bound(a+i+1,a+cnt+1,mid-a[i])-a;
		if(it==cnt+1) continue;
		while(vis[it]&&it<cnt) it++;
		if(!vis[it]&&a[i]+a[it]>=mid)
			ans++,vis[i]=vis[it]=1;
	}
	b[x]=0;
	for(int i=1;i<=cnt;i++)
		if(vis[i]==0)
			b[x]=a[i];
}
bool check(int x){
	ans=0;
	dfs(1,0);
	return ans>=m;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
    cin>>n>>m;
	for(int i=1;i<n;i++){
		int a,b,l;cin>>a>>b>>l;
		add(a,b,l),add(b,a,l);
	}
	int l=0,r=1e17;
	while(l<r){
		mid=l+r+1>>1;
		if(check(mid)) l=mid;
		else r=mid-1;
	}
	cout<<l<<'\n';
	return 0;
}
by __H_J_M__
by huangjieming0703

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...