专栏文章
题解:AT_abc428_e [ABC428E] Farthest Vertex
AT_abc428_e题解参与者 7已保存评论 8
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 8 条
- 当前快照
- 1 份
- 快照标识符
- @minkaqbz
- 此快照首次捕获于
- 2025/12/02 03:48 3 个月前
- 此快照最后确认于
- 2025/12/02 03:48 3 个月前
题意:
给你边权为 的一棵树,问这棵树上每个点距离最远的点最大编号。
思路:
很容易想到树的 直径 。
由树直径的定义:
由树直径的定义:
- 树上任意两节点之间最长的简单路径即为树的 直径 。
答案一定是直径的两个端点之一。(定义直径的端点为 , )
- 节点 在直径上:
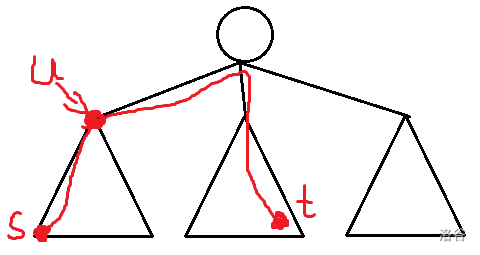
假设距离点 最远的点是 。
如果 不是 或者 那么 就不是直径了。
如果 不是 或者 那么 就不是直径了。
- 节点 不在直径上:
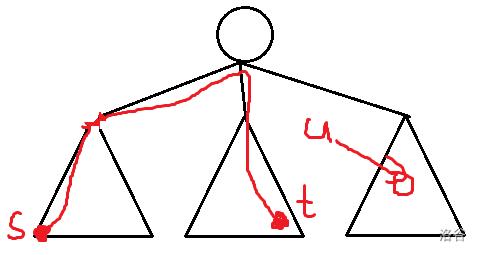
很明显,既然 不在直径上了,那么从那个分开的结点到 一定优于到 , 只有去搭上直径才是最优的 ,其答案等于直径上距离最近的点的答案。
所以写起来就明了了:
找到直径,再维护一个所有点到根的距离 dis ,用 来判断取哪一个直径。
一点细节:
注意到要取编号最大的点,那么维护直径时记得判断编号。
还有不要直接对每个点作 lca 再判断。(我写T了)
可以利用直径上点搜到的非直径部分和该点的答案相同,再搜一遍直接处理答案。
可以利用直径上点搜到的非直径部分和该点的答案相同,再搜一遍直接处理答案。
时间复杂度: 。
找直径 + 倍增求 lca 。
代码:
CPP/*
雲璃猫猫が好きです
すべての生命よ,歌のように輝いています
截剣式、斬、断、破です!
*/
#include<bits/stdc++.h>
#include<bits/extc++.h>
#define int long long
#define INF 1e18
#define lb long double
#define ls (id<<1)
#define rs (id<<1|1)
#define rep(i,l,r,k) for(int i=(l);i<=(r);i+=(k))
#define dep(i,r,l,k) for(int i=(r);i>=(l);i-=(k))
#define tep(x,y) for(auto x:y)
#define wl while
#define mk(a,b) make_pair(a,b)
#define me(a,b) memset(a,b,sizeof(a))
#define pb(x) push_back(x)
#define pr putchar
#define fi first
#define se second
#define max(a,b)((a)>(b)?(a):(b))
#define min(a,b)((a)<(b)?(a):(b))
using namespace std;
random_device rd;
unsigned int seed=rd();
mt19937 Rand(seed);
typedef pair<int,int> pii;
const int M=5e5+110,mod=1e9+7,Mod=998244353;
__gnu_pbds::gp_hash_table<string,int>ml;
inline int read(){int sum=0,k=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')k=-1;c=getchar();
}while(c>='0'&&c<='9'){sum=sum*10+c-48;c=getchar();
}return sum*k;
}inline void wr(int x){if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);return void(putchar(x%10+'0'));}
int n=read(),s,t,dis[M],mx,id,Fa[M][50];//找直径
vector<int>Ed[M];
inline void dfs(int u,int fa,bool ok){
if(ok){//最后一遍再维护倍增数组
Fa[u][0]=fa;
rep(i,1,35,1) Fa[u][i]=Fa[Fa[u][i-1]][i-1];
}
for(auto v:Ed[u]){
if(v==fa) continue;//不往回走
dis[v]=dis[u]+1;
//取最大的编号
if(dis[v]>mx) mx=dis[v],id=v;
else if(dis[v]==mx) id=max(id,v);
dfs(v,u,ok);
}
}
inline int glca(int a,int b){
//倍增求lca
if(dis[a]<dis[b]) swap(a,b);
dep(i,35,0,1) if(dis[Fa[a][i]]>=dis[b]) a=Fa[a][i];
if(a==b) return a;
dep(i,35,0,1)
if(Fa[a][i]!=Fa[b][i]) a=Fa[a][i],b=Fa[b][i];
return Fa[a][0];
}
int ans[M],vis[M];
inline bool fid(int u,int fa){
//将直径路上的点打上标记
if(u==t){
ans[u]=s;vis[u]=1;
ans[s]=u;vis[s]=1;
return 1;//是直径
}
for(auto v:Ed[u]){
if(v==fa) continue;
if(fid(v,u)){//是直径
int ds=dis[u]+dis[s]-dis[glca(u,s)]*2,
dt=dis[u]+dis[t]-dis[glca(u,t)]*2;
if(ds>=dt) ans[u]=s;
else ans[u]=t;
vis[u]=1;
return 1;
}
}return 0;
}
inline void gans(int u,int fa,int wh){
ans[u]=wh;//维护答案
for(auto v:Ed[u]){//不搜直径上点
if(v==fa||vis[v]!=0) continue;
gans(v,u,wh);
}
}
signed main(){
rep(i,1,n-1,1){
int u=read(),v=read();
Ed[u].pb(v);Ed[v].pb(u);
}
//找直径
dfs(1,0,0);s=id;mx=0;id=0;
dfs(s,0,0);t=id;mx=0;id=0;
//这里我保证了当s,t距离一样时选s优
if(s<=t) swap(s,t);
dfs(1,0,1);
fid(s,0);
rep(i,1,n,1)
if(vis[i]!=0) gans(i,0,ans[i]);
rep(i,1,n,1) wr(ans[i]),pr(10);
return 0;
}
相关推荐
评论
共 8 条评论,欢迎与作者交流。
正在加载评论...