P8182 「EZEC-11」雪的魔法

线性规划对偶，变成给每个位置赋 $-1,0,1$ 权，使得任意长度 $\le m$ 区间和 $\le 1$，然后最大化带权和。这个限制换句话说，就是任意距离 $< m$ 的相邻 $1$ 之间要有恰好一个 $-1$。

把序列在相邻且距离 $\ge m$ 的 $1$ 处劈开，则劈出来每一段里去掉 $0$ 之后都是 $1,-1$ 交替的形式。通过手玩，或者直接注意到这就是 $n=m$ 的情况，我们发现这样的一段的最大权值是 $a_1+\sum_{i \ge 2}\max(0,a_i-a_{i-1})$。

考虑这样劈出来的段长啥样：最优解里，第一段一定以序列开头为开头，最后一段一定以序列结尾为结尾，剩下的每相邻两段距离一定恰好是 $m$。把所有除了第一段以外的的左端点取出来，则一个左端点的贡献可以推出来是 $b_i=a_i-\sum_{j=0}^{m-1}\max(0,a_{i-j}-a_{i-j-1})$。

问题变为：在 $[l+m,r]$ 选取若干个点，每个点有点权 $b$，选的任意两个点距离至少为 $m$，最大化点权和。容易写出 DP，$f(i)$ 从 $f(i-m)$ 和 $f(i-1)$ 转移过来，复杂度 $O(nq)$。

考虑建一张图，$i$ 向 $(i+1)$ 和 $(i+m)$ 连边，则它应该几乎是一张网格图：

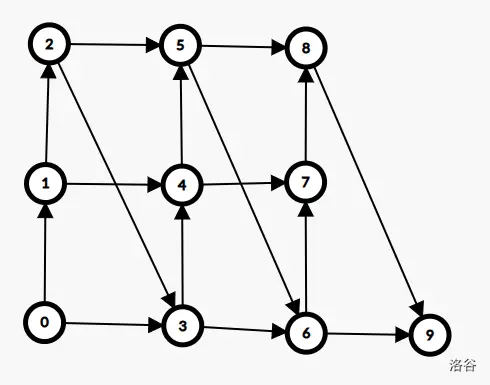
（图片来自 P9040 洛谷题解）我们要在这样的图上多次询问两点最长路。这是可以分治做的。

具体地，我们每次选择网格较长的一边劈开，然后对于分界线上每个点，处理经过它的最短路。因为较短的边长是根号的，主定理一下可以发现总复杂度 $O((n+q) \sqrt n)$。注意这里除了网格边以外还有 $(2,3)$ 这样的斜着的边，这只会在我们第一次对行分治时有贡献，特殊处理一下即可。