数据结构之线段树

算法简介

线段树是一种用于处理区间信息的二叉树。它可以支持单点修改、区间修改、区间查询操作。一般地，线段树的时间复杂度为

O(m\log n)

。

算法实现

建树

在一个序列中，我们将其中的元素看作二叉树的叶子节点，然后向上构建虚拟节点，虚拟节点表示其儿子所在的区间。

如图，其中父节点的权值为其左儿子和右儿子权值之和。

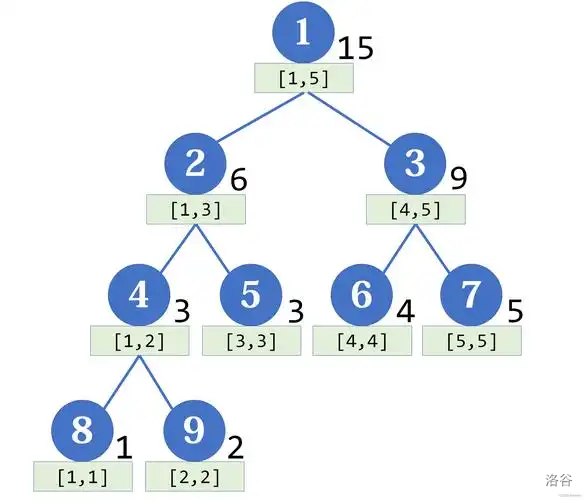
我们不难看出父节点代表的区间，就是其两个子节点所在区间的集合（是这么说的吧？）就比如图中的

4

号节点所表示的区间就是它的儿子——

8,9

号节点所在区间的集合。

注意：建树一般需要开 $4n$ 大小的数组（ $n$ 为原序列长度）。

修改

我们以修改区间

[l,r]

中的元素为例。考虑朴素算法，将每个元素循环修改一次的话，时间复杂度为

O(mn)

（其中

n

为元素个数，

m

为操作次数），非常难受。

现在我们引入线段树的核心出装——懒惰标记（

LazyTag

）。~~顾名思义，它非常懒~~它的原理就是在节点上打一个标签，将操作后修改的信息存在标签上，等到下一次访问带标记的节点后再修改元素。可以结合分块思想中的懒惰标记（这篇中写的是延迟标记，一个意思）进行理解。

查询

我们以查询区间

[l,r]

中的元素为例。考虑朴素算法，将每个元素查询一遍的话，时间复杂度为

O(mn)

，显然不太行。

还记得建树部分中父子节点之间的关系吗？

父节点代表的区间，就是其两个子节点所在区间的集合。

如果我们要查询区间

[l,r]

的话，我们只需要找到包括

[l,r]

区间的所有节点就可以了。显然，这样的节点最多只会有

\log n

个，所以时间复杂度可以优化为

O(m \log n)

。

模板题

P3372 【模板】线段树

代码

CPP

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=100005;
ll n,m,op,x,y,k,mid;
ll tree[N<<2],add[N<<2],a[N];
// tree 是线段树节点，add 是懒惰标记，a 是原序列
void build(ll x,ll l,ll r) // 建树
{
	if(l==r)
	{
		tree[x]=a[l]; // 如果是叶子节点，权值就是序列元素
		return;
	}
	ll mid=(l+r)>>1;
	build(x<<1,l,mid); // 在左子树上建树
	build((x<<1)+1,mid+1,r); // 在右子树上建树
	tree[x]=tree[x<<1]+tree[(x<<1)+1]; // 回溯时计算该节点的权值
}
void drop(ll x,ll l,ll r,ll k)
{
	add[x]+=k; // 懒惰标记对节点进行延迟修改
}
void push_down(ll x,ll l,ll r) // 下放懒惰标记
{
	ll mid=(l+r)>>1;
	drop(x<<1,l,mid,add[x]); // 向左子树下放
	drop((x<<1)+1,mid+1,r,add[x]); // 向右子树下放
	tree[x]+=(r-l+1)*add[x];  // 懒惰标记对节点进行延迟修改
	add[x]=0; // 清空懒惰标记
}
void upd(ll x,ll begin,ll end,ll l,ll r,ll k) // 修改
{
	if(begin>r||end<l) // 如果节点在区间外，直接返回
		return;
	if(begin>=l&&end<=r) // 如果在节点内，对懒惰标记进行修改
	{
		add[x]+=k;
		return;
	}
	ll mid=(begin+end)>>1;
	push_down(x,begin,end); // 下放懒惰标记
  upd(x<<1,begin,mid,l,r,k); // 修改左子树
  upd((x<<1)+1,mid+1,end,l,r,k); // 修改右子树
  tree[x]=tree[x<<1]+tree[(x<<1)+1]+(mid-begin+1)*add[x<<1]+(end-mid)*add[x<<1|1];
  // 计算该节点的权值
} 
ll query(ll x,ll begin,ll end,ll l,ll r)
{
	if(begin>r||end<l) // 跟上面一样的判断区间
		return 0;
	if(begin>=l&&end<=r)
		return tree[x]+(end-begin+1)*add[x]; // 查询区间
	ll mid=(begin+end)>>1;
	push_down(x,begin,end); // 访问的同时推懒惰标记
	return (ll)query(x<<1,begin,mid,l,r)+(ll)query((x<<1)+1,mid+1,end,l,r); // 返回区间内节点的权值之和
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	build(1,1,n);
	while(m--)
	{
		cin>>op>>x>>y;
		if(op==1)
		{
			cin>>k;
			upd(1,1,n,x,y,k);
		}
		if(op==2)
			cout<<(ll)query(1,1,n,x,y)<<endl;
	}
	return 0;
}

THE

END

数据结构之线段树

文章操作

算法简介

算法实现

建树

修改

查询

模板题

代码

相关推荐

评论

数据结构之线段树