定义一棵边有颜色的树的不方便度为其颜色最多的简单路径的颜色数。

给定一棵 $n$ 个点的树，对于每个 $k\in[1,n-1]$ 求当用恰好 $k$ 种颜色（每种都出现）给边染色时该树不方便度的最小值。

数据范围：多测，$\sum n\le3\times10^5$。

下述距离、路径长度等词一律按边数而非点数。

考虑 $k=n-1$ 的情况，此时答案就是直径。容易想到不方便度的本质就是在颜色数定义下的直径。而直径的中点就是到所有点的最大距离最小的点，此时明显直径长为偶数时的情况比较简单，直径中点到各点间距离均不超过 $\frac{k}{2}$。

从此入手，就是让最外 $\frac{k}{2}-1$ 层每条边分配一种颜色，加上这些层与我们钦定的根结点间的边还要染一种，总共就是所有点到根结点都不超过 $\frac{k}{2}$ 种颜色。由于此时可以钦定任何剩下的点为根结点，所以我们肯定要取度数最大的，因为根据我们刚才的设定每个度数都可以染一种颜色。

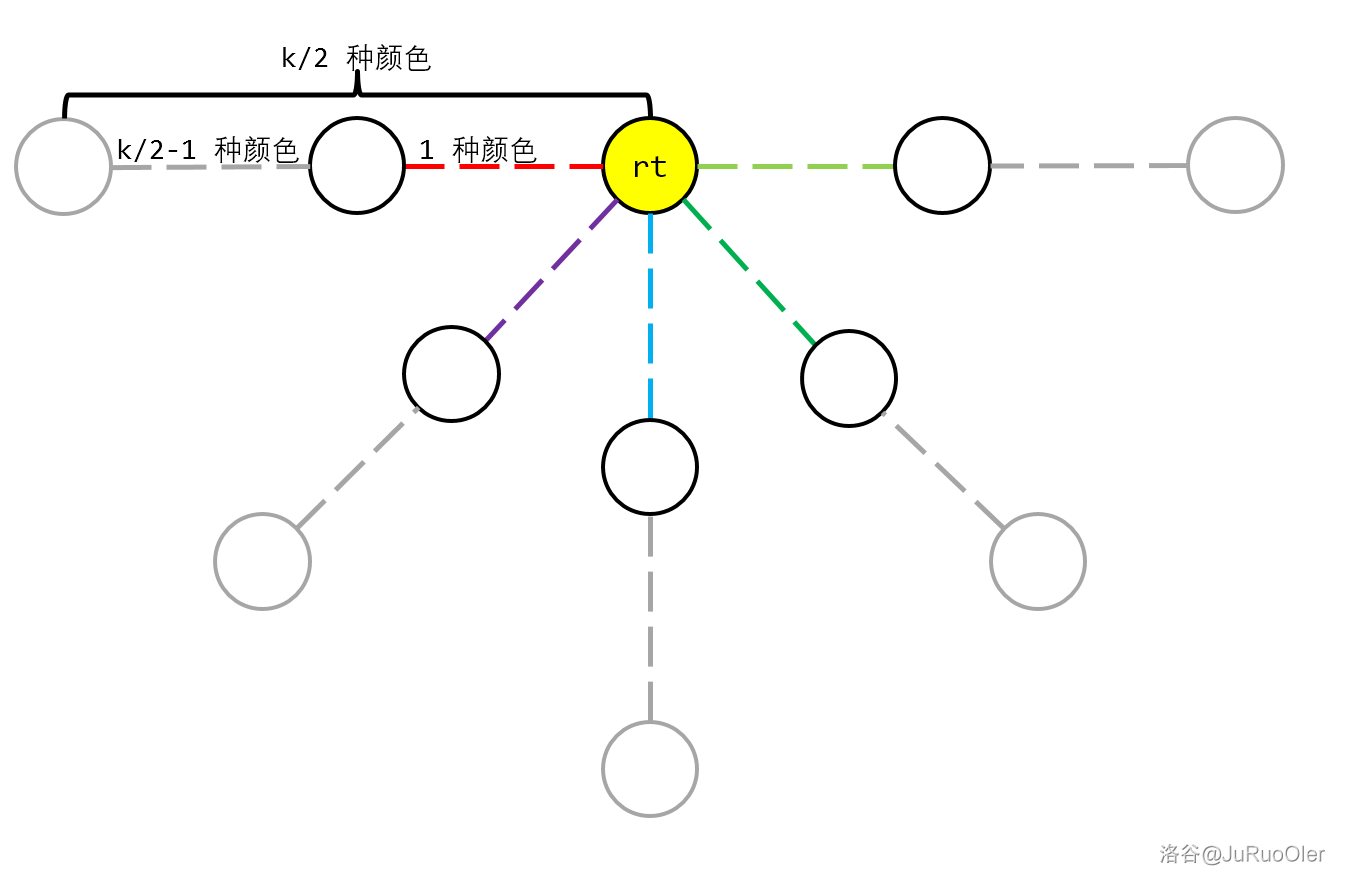
图中虚线表示多个点，灰色的点是被删掉的。

而奇数的情况比较类似，不过此时中点在边上。所以我们让这个边所在的颜色块贡献 $1$ 的答案，于是该颜色块到其他点之间的距离就是不超过 $\frac{k-1}{2}$ 了。

实现时用类似多源 BFS 的方式剥叶子即可。复杂度 $O(n)$。