专栏文章
AT_tenka1_2018_e Equilateral 题解
AT_tenka1_2018_e题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @miqyazh1
- 此快照首次捕获于
- 2025/12/04 12:43 3 个月前
- 此快照最后确认于
- 2025/12/04 12:43 3 个月前
You can view the English version of this solution.
图片托管于 Github,若加载失败请使用加速器。
考虑画出三个点的哈夫曼距离。
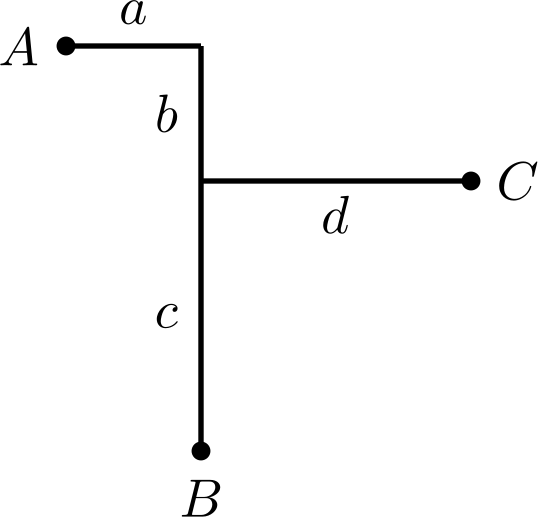
则有 ,即 。这也就是说, 的斜率为 ,而 在与之平行的一条线上。
我们不妨 枚举 , 枚举 ,通过差分 计算合法的 的数量。复杂度 ,有较大常数。
具体的,我们枚举 和 ,问题转化为求四条线上 的个数。对每条斜率为 的直线预处理出前缀和即可。

需要注意,为了避免算重,不妨将特殊的端点位置单独计算。
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...