专栏文章
题解:CF1814F Communication Towers
CF1814F题解参与者 3已保存评论 2
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 2 条
- 当前快照
- 1 份
- 快照标识符
- @mipen0q6
- 此快照首次捕获于
- 2025/12/03 10:45 3 个月前
- 此快照最后确认于
- 2025/12/03 10:45 3 个月前
巨佬们怎么都打的线段树分治?!
一种很清奇的思路:树状 DP
(虽然这是个图,但感觉叫它树状也没啥问题)
或者说这个算法是 DFS。
我们先看一下下面这个样例:
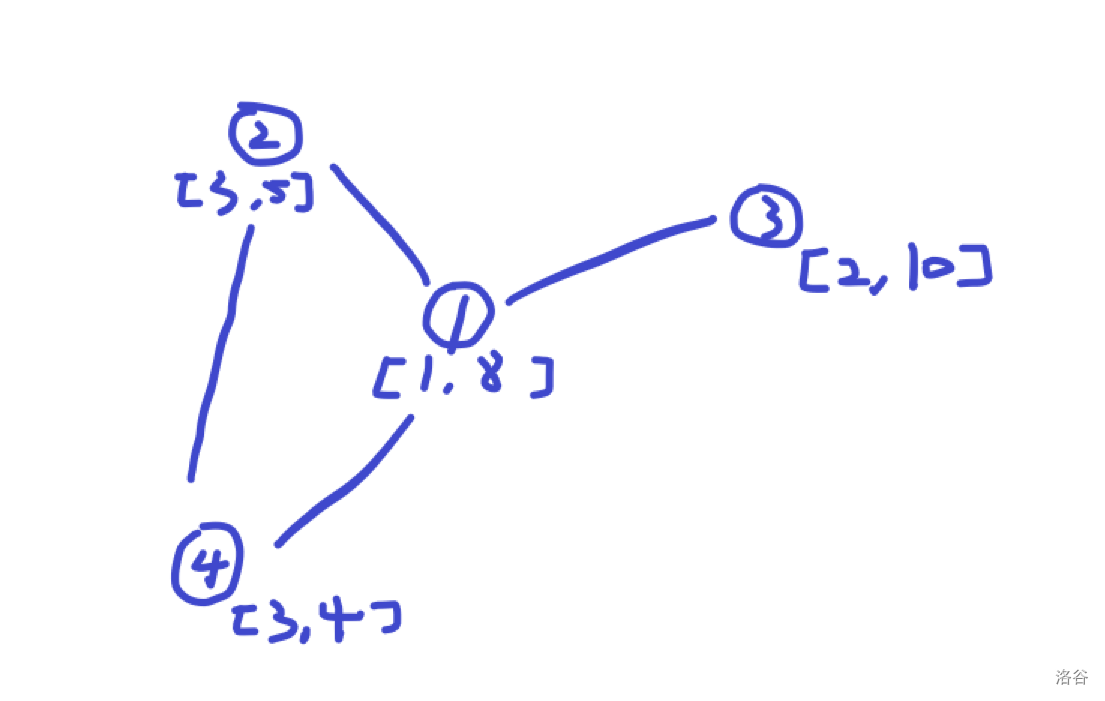
每个圆圈里的数字代表编号,下面的中括号代表工作频率。
重审题意,要求只要在某一频率下一个点能和 联通,那么就属于答案。
那么我们就可以从点 开始,带着点 的频率来 DFS。
比如说,我们来到了 号点,发现 号点在 的频率下可以工作。
那么我们取点 和点 共同包含的频率:。表示在频率 下点 和点 可以连通。
再从点 以 的频率往外 DFS,直到到某个点没有共同覆盖的频率,这时候停止。途中经过的点就都算作答案。
再从点 向点 拓展,取到共同覆盖频率 。
大体思路是这样,但我们需要考虑出口和剪枝。
比如我们从点 走点 来到了点 ,频率为 ,但是我们之前已经从点 以 的频率往外搜索过了, 包含在了 里面,再往下搜是没有意义的,所以剪枝掉。
但我们如果以 的频率来到了点 ,此时这段频率不全覆盖在之前的 中,所以我们以 的频率往下搜索尝试得到新答案。
到这里思路就已经结束了,理论可行,上代码:
Code
CPP#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e5 + 5, M = N << 1;
int n, m;
bool ans[N];
vector <int> road[N];
vector <pair <int, int>> once[N];
inline pair <int, int> get (int p, pair <int, int> x) {
x.first = max(x.first, once[p][0].first),
x.second = min(x.second, once[p][0].second);
for (int i = 1; i < once[p].size(); i ++) {
pair <int, int> th = once[p][i];
if (th.first <= x.first and th.second >= x.second) return {-1, 0};
else if (th.first > x.second or th.second < x.first) continue;
else if (x.first < th.first and x.second <= th.second) {
x.second = th.first - 1;
}
else if (th.first <= x.first and th.second < x.second) {
x.first = th.second + 1;
}
}
return x;
}
void dfs (int p, int Jn, pair <int, int> now) {
pair <int, int> g = get(p, now);
if (g.first == -1) return;
if (g.first > g.second) return;
once[p].push_back(g);
ans[p] = 1;
for (int i = 0; i < road[p].size(); i ++) {
if (road[p][i] != Jn) dfs(road[p][i], p, g);
}
}
int main () {
cin >> n >> m;
int u, v;
for (int i = 1; i <= n; i ++) {
cin >> u >> v;
once[i].push_back({u, v});
}
for (int i = 1; i <= m; i ++) {
cin >> u >> v;
road[u].push_back(v);
road[v].push_back(u);
}
dfs(1, 0, once[1][0]);
for (int i = 1; i <= n; i ++) {
if (ans[i]) cout << i << ' ';
}
return 0;
}
相关推荐
评论
共 2 条评论,欢迎与作者交流。
正在加载评论...