前言
21 世纪最重要的品质——淡定
什么是调整法?
调整法,顾名思义,就是在已有决策上调整,通过对原决策和调整后决策的比较,排除对答案没有用的情况,保留真正有价值的情况。调整法适用于一系列的最优化问题和证明问题。
设
f(x)=xlnx,若
x1,x2∈(0,1),证明:
∣f(x1)−f(x2)∣≤h(∣x1−x2∣)。
其中
h(x) 是一个满足随
x 单调递增的函数,大部分题目中
h(x)=x,本题中
h(x)=x。
前置准备:
| f(x) | f′(x)=lnx+1 |
|---|
 | 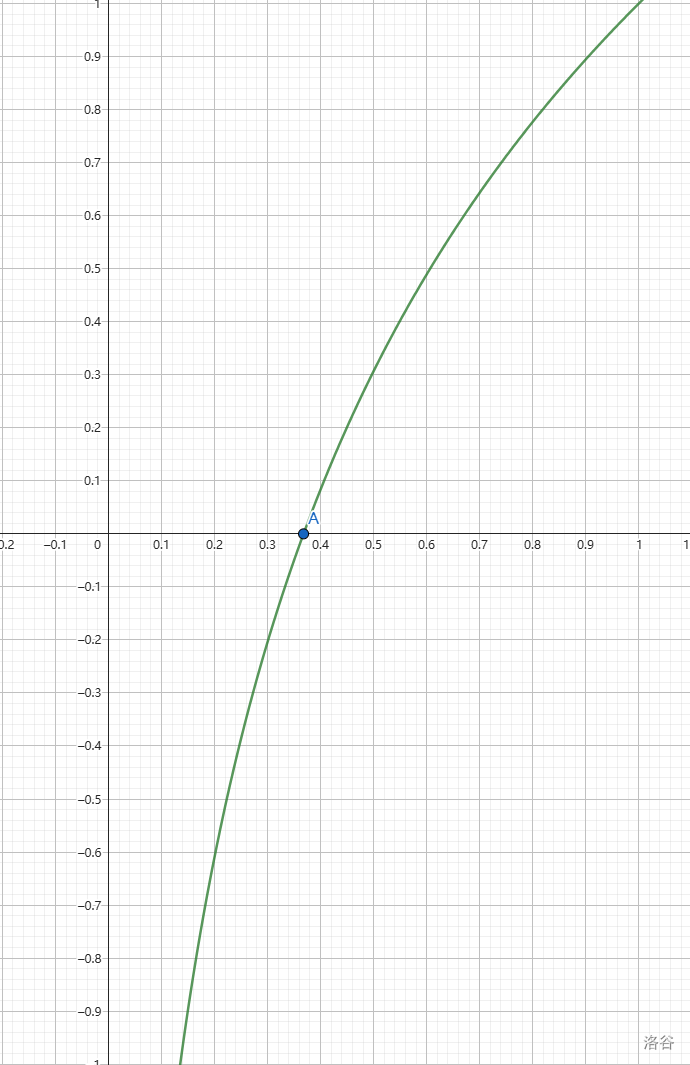 |
根据洛必达原理,
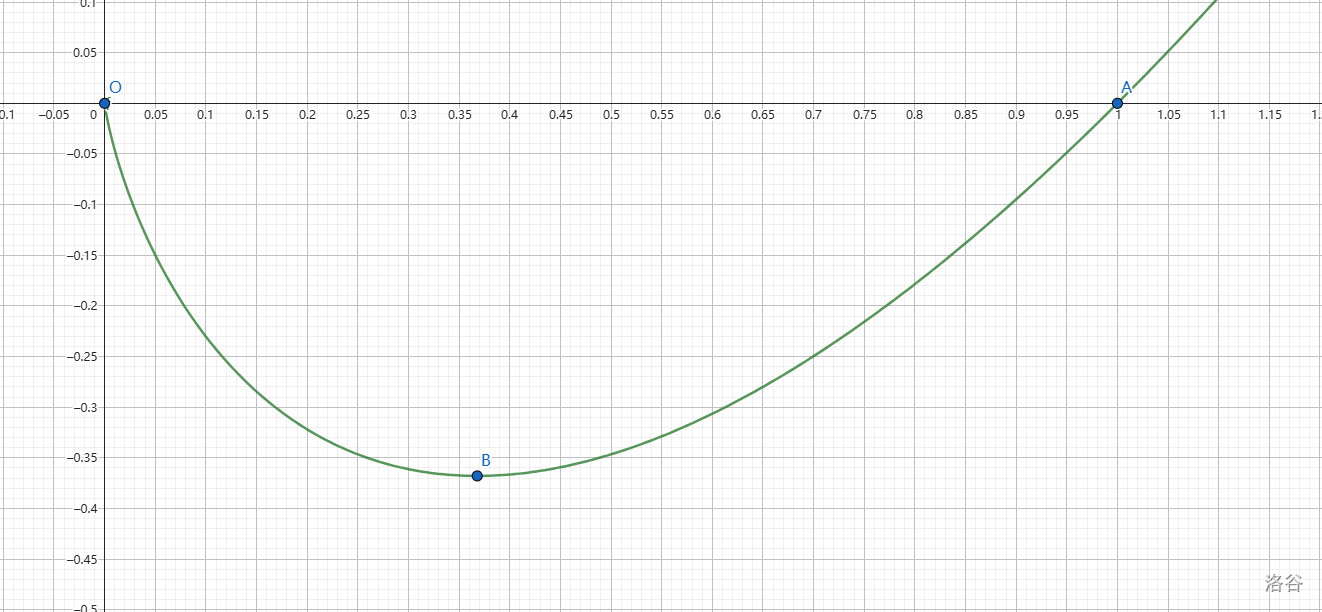
limx→0f(x)=limx→0x1lnx=limx→0−x21x1=0,
f(1)=0,极值点
B(e1,−e1)。
第一步调整
我们先证明:
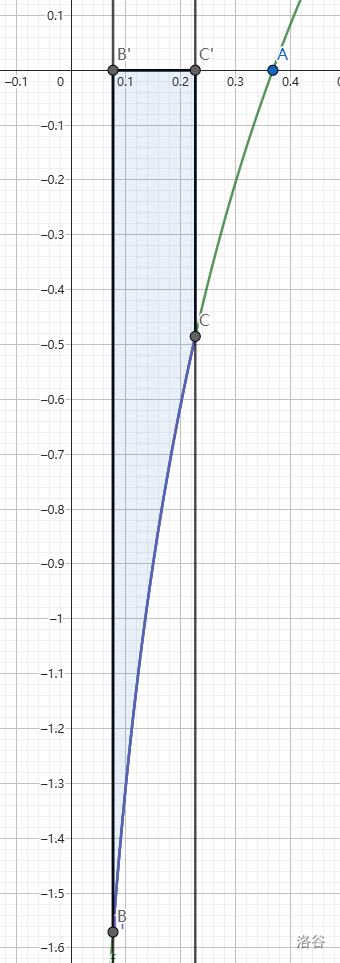
当 x2>e1,x1≤e1 时(也就是 x1,x2 分别在极值点两侧时)的情况不影响答案。| 图 1 | 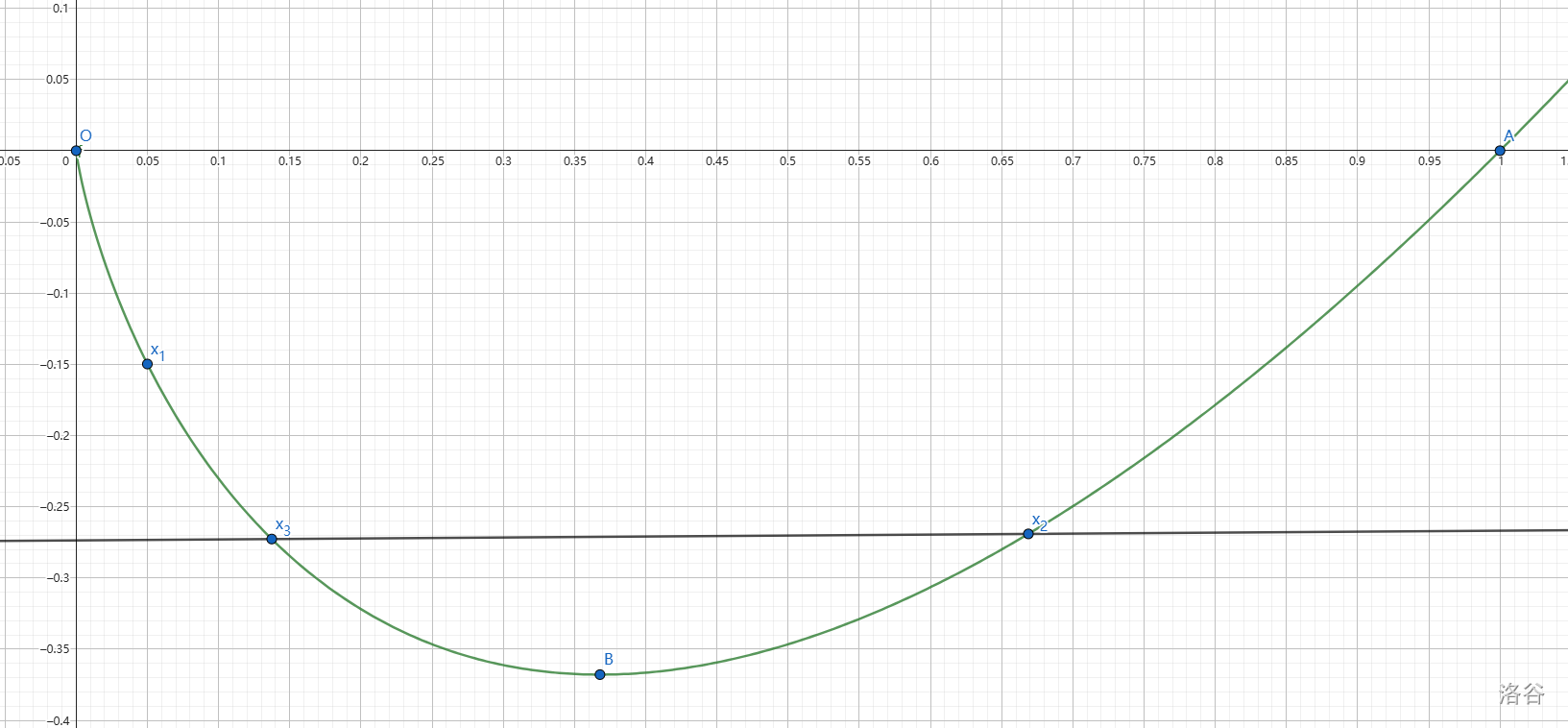 |
|---|
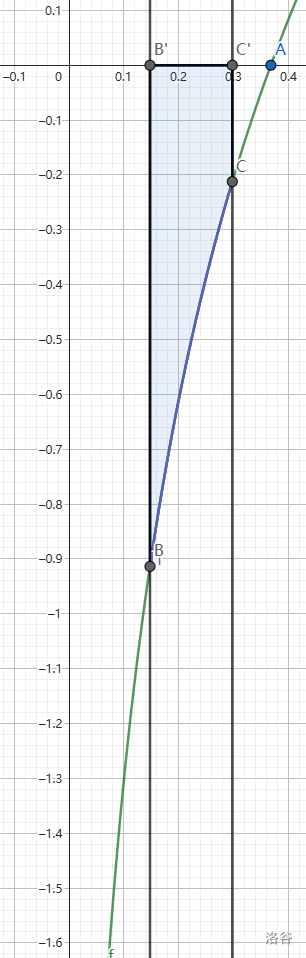
| 图 2 | 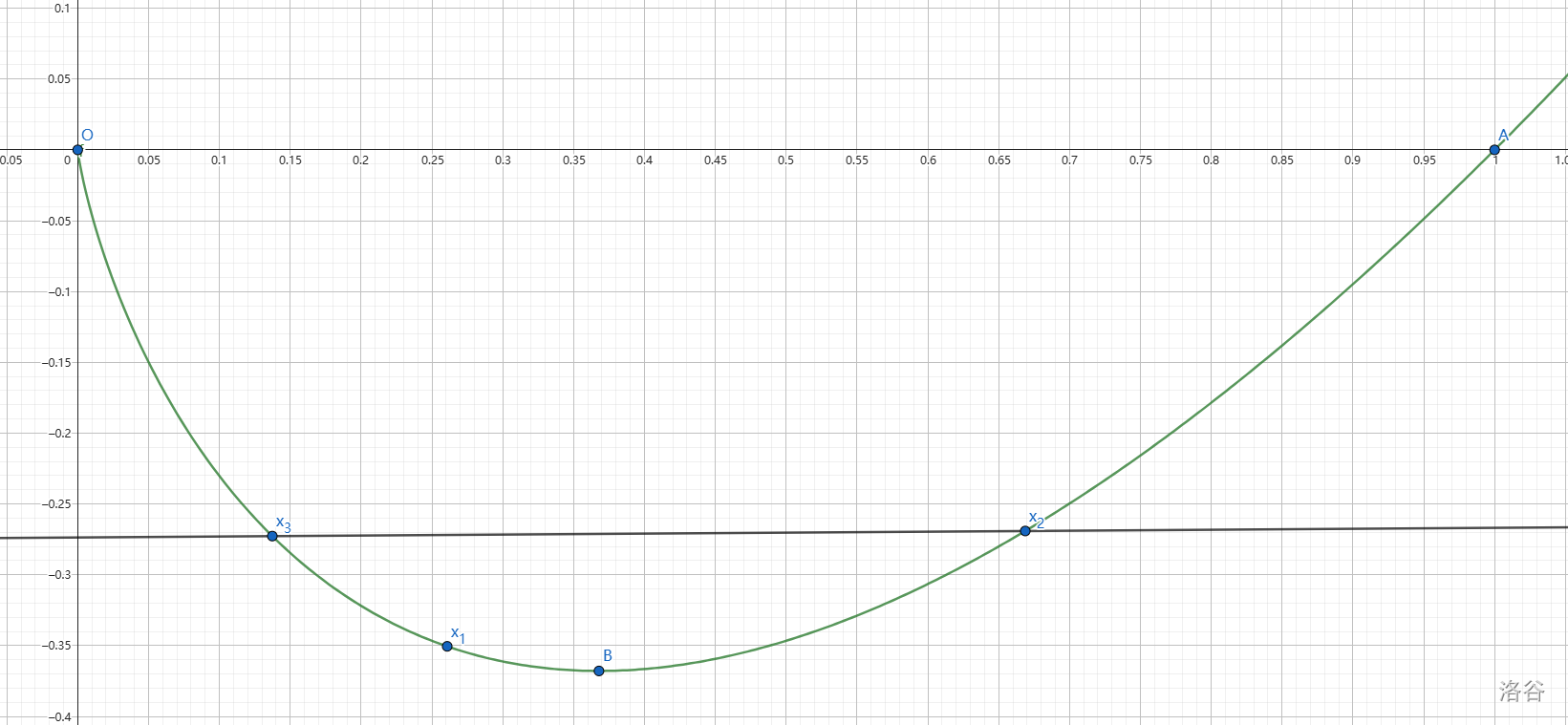 |
找到一个点
x3 满足
x3<e1 且
f(x2)=f(x3)。如图 1,当
x1<x3 时,显然有
∣x1−x3∣<∣x1−x2∣。也就是说,
如果 ∣f(x1)−f(x3)∣<h(∣x1−x3∣),那么必然有 ∣f(x1)−f(x2)∣<h(∣x1−x2∣)。
但如果
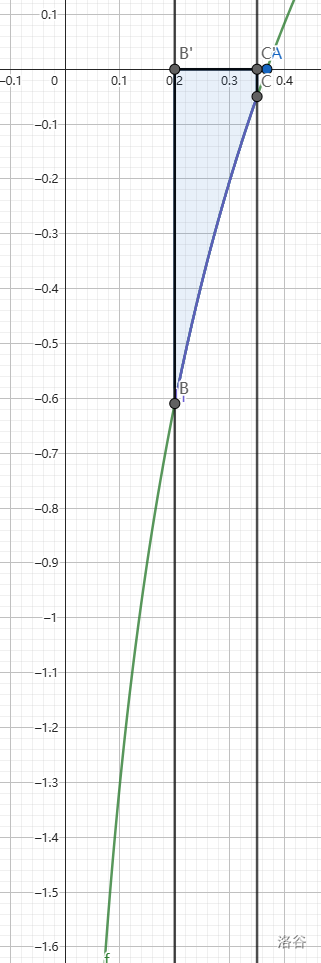
x1>x3(图 2)时,是否还能有
∣x1−x3∣<∣x1−x2∣ 这么好的性质呢?当然有。
我们先证明一个极值点偏移:
引理:x2+x3>e2。 这个引理的等价表述是
∣x2−e1∣<∣x3−e1∣。
即证
x2>e2−x3。因为
x3∈(0,e1),所以
e2−x3>e1,它们都在极值点右侧,所以可以转化为
f(x2)>f(e2−x3),即
f(x3)>f(e2−x3)。
令
F(x)=f(x)−f(e2−x) (x∈(0,e1]),
F′(x)=lnx+ln(e2−x)+2=ln(x⋅(e2−x))+2。
根据均值不等式,
x⋅(e2−x)≤e21,所以
F′(x)≤ln(e21)+2=0,所以
F(x)≥F(e1)=0。
又因为
x3<e1,有
f(x3)>f(e2−x3),即
x2+x3>e2 成立。
所以,我们有:
∣x1−x2∣≥∣x2−e1∣≥∣x3−e1∣≥∣x1−x3∣。性质仍然成立。
综上,所有
x1,x2 横跨极值点的情况都不优于
x1,x2 在同一侧的情况,不用再讨论下去。
第二步调整
我们接着讨论
x2≤e1 的情况。首先进行感性理解:
观察
f′(x) 的图像,我们发现如果固定了
∣x1−x2∣ 的值,那么它们对应点围成的曲面梯形面积随着
x1 的右移在不断减小,也就意味着
∣f(x2)−f(x1)∣ 在越来越小。根据调整法,我们应该要尽量让这个值大一些,把情况往最严格的地方卡。因此,我们如果能够证明
∀x∈(0,e1],都有
∣f(x)∣≤h(x) 的话,整个
x2≤e1 都是合法的。
x1≥e1 的情况也是如此,如果能够证明
∀x∈[e1,1),都有
∣f(x)∣≤h(1−x) 的话,这一部分的情况也都是合法的。
下面我们来理性证明一下:
引理:∣f(x1)−f(x2)∣≤∣f(x2−x1)∣。
法一: 由于
f′(x)=lnx+1 单调递增且在
(0,e1) 内的值
<0,所以
∀x∈(x1,e1) 都有
f′(x)>f′(x−x1)。
所以有
∣0x2−x1f′(x)<∣x1x2f′(x),即
f(x2−x1)<f(x2)−f(x1)。又因为
f(x) 在
(0,e1) 单调递减且值恒小于 0,所以有
∣f(x1)−f(x2)∣≤∣f(x2−x1)∣。
法二: 令
x1=a,x2−x1=b,即证
f(a)+f(b)≤f(a+b)。也就是
alna+blnb≤(a+b)ln(a+b)。同时取对数,
ealna+blnb=(elna)a×(elnb)b=aa×bb,同理
e(a+b)ln(a+b)=(a+b)a+b。
根据均值不等式,
aa×bb≤(a+ba2+b2)a+b=(a+b−a+b2ab)a+b<(a+b)a+b,成立!
根据调整法,如果
∣f(x2−x1)∣≤h(∣x2−x1∣),那么一定有
∣f(x1)−f(x2)∣≤h(∣x2−x1∣)。所以我们只需要讨论
∣f(x)∣ 与
h(x) 的大小关系即可。
对于
x1≥e1 的情况同理,可以证明
∣f(x1)−f(x2)∣≤∣f(1)−f(1−∣x1−x2∣)∣,只需判断
f(x) 与
h(1−x) 的大小关系即可。
最后的计算
- Part 1:证明 −xlnx<x (x∈(0,e1])
即证
xlnx>−21。令
t=x∈(0,ee),即证
tlnt>−21。这不就是
f(t) 吗?显然有
−e1>−21,成立!
- Part 2:证明 −xlnx<1−x (x∈[e1,1))
即证
x2ln2x<1−x,即证
ln2x+x1−x21<0(设为
g(x))。
g′(x)=x2lnx−x21+x32=x31(2x2lnx−x+2)。考虑分析
φ(x)=2x2lnx−x+2。利用对数均值不等式
lnx>x+12(x−1),
φ(x)>2x2x+12(x−1)−x+2=(x+1)[4x2(x−1)+(x+1)(2−x)]=(x+1)[4x3−5x2+x+2]。分析
y=4x2−5x+1,对称轴为
x=85,此时
y=−259,那显然
y>−2,所以
φ(x)>0,
g′(x)>0,只需要考虑
x=1 的情况,恰好
g(1)=0,成立!
(相信有更加简单的办法)
综上,
∣f(x1)−f(x2)∣≤h(∣x1−x2∣),成立!