专栏文章

#3338. tree

DDE_aemmprty
个人记录参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@minhvbna
此快照首次捕获于
2025/12/02 02:40
3 个月前
此快照最后确认于
2025/12/02 02:40
3 个月前
查看原文
有一个 nn 个节点的树，每个节点上有一个颜色 aia_i，令 fi,jf_{i, j} 表示节点 ii 到节点 jj 的路径上所有点的不同颜色数量。现在给你一个 n×nn\times n 的二维数组，请你找到一个树和一个颜色方案能得到输入的 ff 数组，保证有解。

Preperation\mathbf{Preperation}

这题可能是怎么做的。
  • 观察部分分，有只考虑链的情况。我们可以先不考虑树的结构，只单纯思考颜色的构造。
  • 当颜色数特别少的时候，如何构造？

Lemma\mathbf{Lemma}

Lemma.1\mathbf{Lemma. 1}
如果一个 xx 能通过同一个点权到达 SS，那么对于所有 x,y∈Sx, y \in S，都有 fx,y=1f_{x, y} = 1。
推论：不存在 x∈S,y∉Sx \in S, y \notin S，fx,y=1f_{x, y} = 1。
Lemma.2\mathbf{Lemma. 2}
对于两个同色集合 A,BA, B，有所有 x∈A,y∈Bx \in A, y \in B，fx,yf_{x, y} 都相等。

Question.1\mathbf{Question. 1}

颜色数最多两种时，如何构造？
ANSWER\mathbf{ANSWER}
先随便选一个点 xx，那么与 xx 相连的点集被分为 A,BA, B，其中 AA 是一种，BB 是两种。
AA 集合里的点肯定 cxc_x 相等，那么 AA 与 xx 向外连的路径一定都是 22。
我们先拉出若干条边权为 11 的链，再用 22 连起来即可。

Question.2\mathbf{Question. 2}

当存在链的解时，如何构造？
Mistake\mathbf{Mistake}
场上没看到 i→i+1i \to i + 1，导致被误导，认为每次还要特地去寻找新的结点，并判定是否能接到链的末尾。
还是实力问题！
ANSWER\mathbf{ANSWER}
假设我们已经求出了 11 到 xx 的颜色是什么，现在要加入第 x+1x + 1 个点。
考虑 fi,xf_{i, x} 和 fi,x+1f_{i, x + 1}。如果这两个数相等，说明 cx+1c_{x + 1} 在 [i,x][i, x] 中出现过了，否则就是没出现过。
我们找到最后一个 ii，使得 fi,x=fi,x+1f_{i, x} = f_{i, x + 1}，那么，由于 cx+1c_{x + 1} 在 [i,x][i, x] 出现而不在 [i+1,x][i + 1, x] 出现，我们有 ci=cxc_i = c_x。
如果全部都不相等，就设 cx+1=x+1c_{x + 1} = x + 1。若有解那么这一定是可行的。

Question.3\mathbf{Question. 3}

Question.2\mathbf{Question. 2} 的 ANSWER\mathbf{ANSWER} 能不能扩展？换句话说，能否在一般的树上找到一个染色方法？
ANSWER\mathbf{ANSWER}
我们考虑将链上的做法放到树上。
假设我们当前考虑到 vv，然后我们要找到一个 fi,u=fi,vf_{i, u} = f_{i, v} 且 fi′,u≠fi′,vf_{i', u} \neq f_{i', v}，这时一定有 cv=cic_v = c_i。
对于这个，我们枚举 u,vu, v，然后从 uu 开始 DFS，如果遇到了合法的 ii，就不往下 DFS 了。

Question.4\mathbf{Question. 4}

如何找到一个合法的树？
ANSWER\mathbf{ANSWER}
如果 fu,v=1f_{u, v} = 1，由 Lemma.1/2\mathbf{Lemma. 1 / 2}，我们可以把他们压起来。因此，我们可以默认 fu,v>1f_{u, v} > 1。
首先，一条合法的树边 u→vu \to v，fu,vf_{u, v} 肯定为 22。但是可能有很多的 fu,v=2f_{u, v} = 2，所以似乎不知道要选哪一些边。
现在，有结论：原题存在解等价于对于任意一个 fu,v=2f_{u, v} = 2 的 (u,v)(u, v) 组成的生成树，该树存在解。
Prove\mathbf{Prove}(感性理解)
我们观察 fu,v=2f_{u, v} = 2 的 (u,v)(u, v) 点对。实际上，如果有一个 fu,v=2f_{u, v} = 2，那在 uu 到 vv 的路径上的任意两个点 x,yx, y，都有 fx,y=2f_{x, y} = 2。
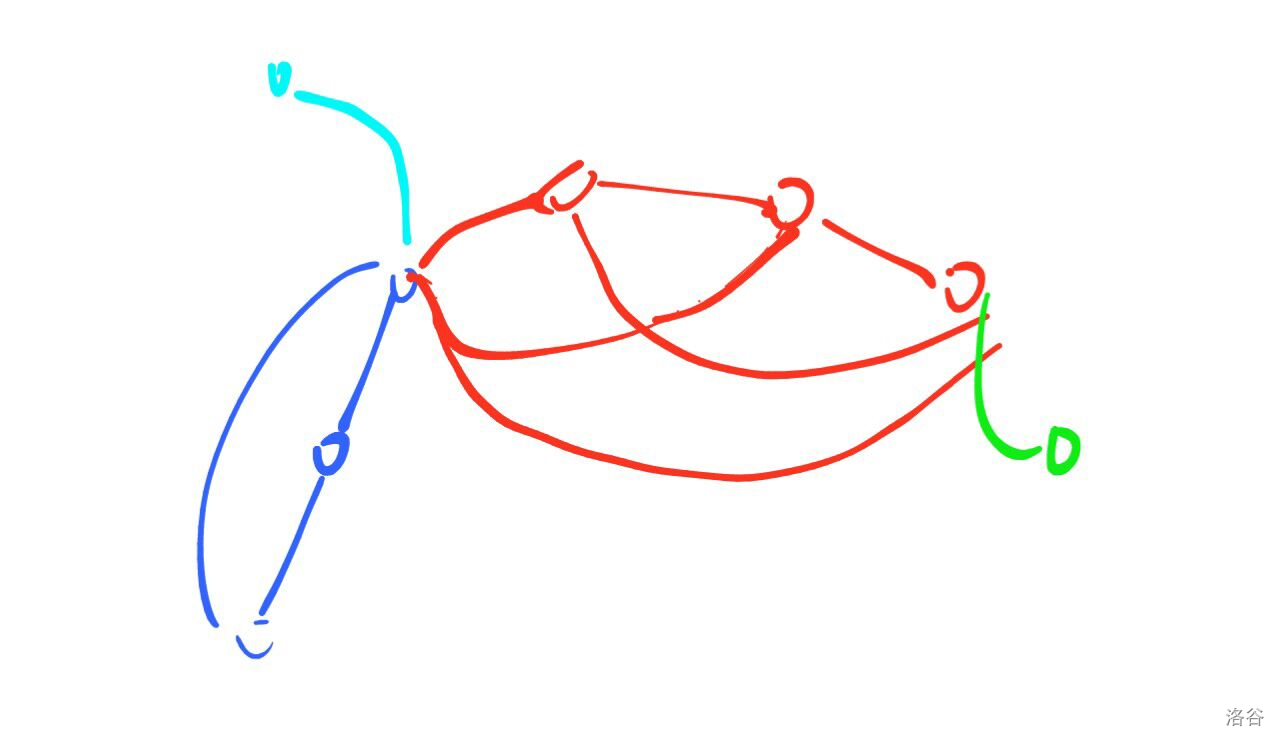
也就是说，这个图实际上是若干个团连接在了一起，如下图：
因此，每个团之间是互相独立的。我们单独考虑每个团，假设团的点集为 SS，该团的两种点权分别是 a,ba, b。
我们考虑所有 xx 向 yy 的经过 SS 的路径，这时有两种可能：
  • 只经过了 SS 中的一个点 tt，这时经过的边一定与该团无关，与 ctc_t 有关
  • 经过了 SS 中的一条边，这时路径只与该团的两种权值 a,ba, b 有关
因此，其实对于一个团内的连边方式并不重要，我们任取一个生成树即可。
通过这个结论，我们可以随便找一颗 fu,v=2f_{u, v} = 2 的生成树，然后跑 Question.3\mathbf{Question. 3} 的染色方法即可。

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...