常数访问块状链表(省流：带插分块)

前言

因为长度是严格的，没有块链的许多优良性质，所以适用范围不广。

推荐阅读：~~块状链表~~，分块。

原理

例题

有数组

a

，最初为空。在线地实现以下操作：

求 $a_i$ 。
将 $a_i$ 改为 $x$ 。
在 $a_i$ 前插入 $x$ 。
如果 $i \ge |a|$ ，则表示是从末尾插入。
删除 $a_i$ 。

下标从

0

开始，操作数量

m \le 10^5

。

实际上就是三个操作：访问，插入，删除。访问可以返回引用，实现操作

1,2

。

我们将数组分为若干个长度相等的块，每个块用 deque 维护。
为了简单，做以下约定：

块长定为 $B = 350$ 。
那么，第 $i$ 个元素在第 $i/B$ 块的第 $i \bmod B$ 个。
最后一个块可以有任何不大于 $B$ 的长度。

CPP

vector<deque<int>> a {{}}; // 开始要有一个块

由于我们知道了第

i

个元素的位置，访问自然可以做到

O(1)

。

CPP

int& get(int p) {
  return a[p / B][p % B];
}

通过类似的方式，插入、删除时易找到元素位置。可是，如何维护长度相等的性质呢？

插入

插入一个元素到对应块后，它的长度可能是

B + 1

。

插入平衡（块

i

）

如果 $i$ 是最后一个块，将末尾元素分裂为新的块。
否则，将末尾元素移动到块 $i+1$ 的开头。
如果块 $i+1$ 为 $B+1$ 个元素，对 $i+1$ 递归执行平衡操作。

CPP

void ins(int p, int x) {
  int i = p / B;
  a[i].insert(a[i].begin() + p % B, x);
  // 平衡
  for (int e = a.size(); i < e; ++i) {
    if (i == int(a.size() - 1))
      if(a[i].size() > B) a.emplace_back();
      else break;
    a[i + 1].push_front(a[i].back());
    a[i].pop_back();
  }
}

删除

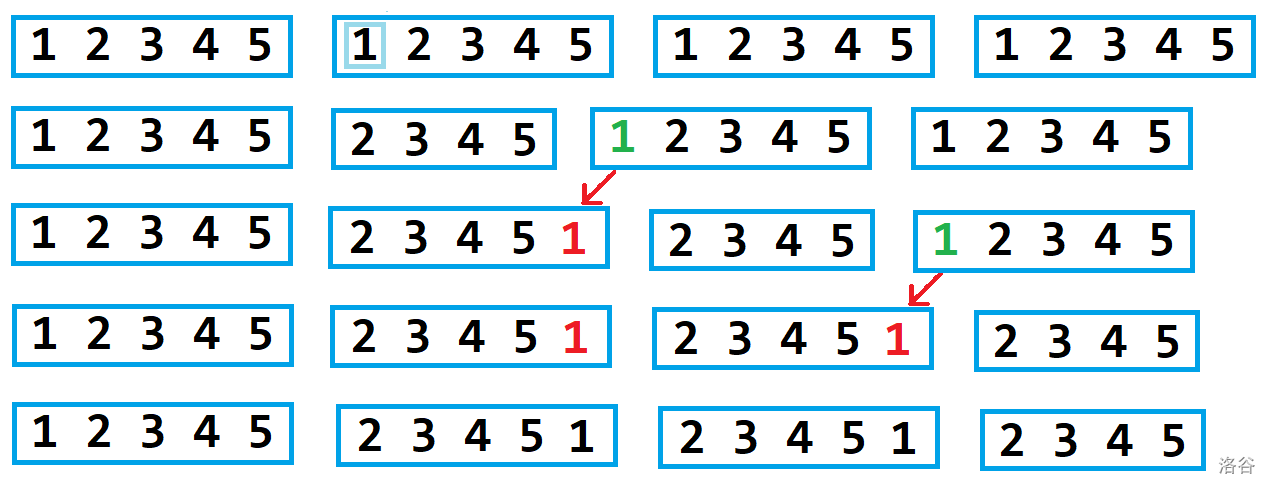
删除一个元素后，非末尾块

i

的长度可能是

B - 1

。
此时，将块

i+1

的开头移动到块

i

的末尾。
如果块

i+1

是非末尾块且长度为

B - 1

，对下一个块递归执行。

CPP

void del(int p) {
  int i = p / B;
  a[i].erase(a[i].begin() + p % B);
  // 平衡
  for (int e = a.size() - 1; i < e; ++i) {
    a[i].push_back(a[i + 1].front());
    a[i + 1].pop_front();
  }
}

实现

CPP

#include <bits/stdc++.h>
#define fo(i,l,r) for(int i=(l),E##i=(r);i<=E##i;++i)
#define N 100005
#define B 350
using namespace std;

struct Arr {
  vector<deque<int>> a {{}}; // 预先设置一个块

  int& get(int p) {
    return a[p / B][p % B];
  }

  void ins(int p, int x) {
    int i = p / B;
    a[i].insert(a[i].begin() + p % B, x);
    // 平衡
    for (int e = a.size(); i < e; ++i) {
      if (i == int(a.size() - 1))
        if(a[i].size() > B) a.emplace_back();
        else break;
      a[i + 1].push_front(a[i].back());
      a[i].pop_back();
    }
  }

  void del(int p) {
    int i = p / B;
    a[i].erase(a[i].begin() + p % B);
    // 平衡
    for (int e = a.size() - 1; i < e; ++i) {
      a[i].push_back(a[i + 1].front());
      a[i + 1].pop_front();
    }
  }
};

//int test() {
//  Arr a;
//  fo (i, 0, 799) a.ins(0, i);
//  fo (i, 1, 20) a.del(20);
//  fo (i, 1, 20) a.del(720);
//  fo (i, 0, 759) cout << a.get(i) << endl;
//}

// 1 询问 2 修改 3 插入 4 删除
int main() {
  int m, op, p, x;
  Arr a;
  cin >> m;
  up (i, 1, m) {
    cin >> op >> p;
    switch (op) {
    case 1: cout << a.get(p - 1) << endl; break;
    case 2: cin >> x; a.get(p - 1) = x; break;
    case 3: cin >> x; a.ins(p - 1, x); break;
    case 4: a.del(p - 1);
    }
  }
}

后记

分裂合并明天不用来了。舒服。

关于可持久化的尝试

在写可持久化块状链表：
可持久化块状数组（分块可持久化）

每个版本维护一个各块长度前缀和的数组（其实就是块头的索引），似乎也可以做到

O(\log n)

的随机访问，而且好写（逃）

发现使用哈希表记录每个索引对应的块也可以，但是可持久化哈希表又是另一个问题。

以上。

常数访问块状链表(省流：带插分块)

文章操作

前言

原理

插入

删除

实现

后记

关于可持久化的尝试

相关推荐

评论

常数访问块状链表(省流：带插分块)