前言

线段树是在 OI 中受到广泛应用的一种数据结构，其变种多，难度较大。作者发现自己对线段树的理解也很糖，故作此文以总结。

作者自己水平太菜，对许多知识点理解不深，讲得也比较肤浅，各位大佬见谅。

各个知识点的 OI-Wiki 链接在题单中有。

对难度 & 实用程度的说明：均

\in[0,10]

（个人向，仅供参考），假设标准懒标记线段树（即线段树 1 模板题）的难度为

3

。

保证知识点经过拓扑排序。

下文默认读者已经掌握线段树基础及懒标记的使用。

权值线段树

评价

难度： $4$
实用程度： $4$

介绍

比较简单的理解：把线段树当桶用。

用线段树来维护某个值的覆盖次数。由于可以实现区修区查，效率较高。

常用于一些简单 DP 的优化（之前 ABC 应该出过几道权值线段树优化 DP，忘记编号了）。

权值线段树是主席树的基础，需要牢固掌握。

例题

~~这个算法太水了，就放一道例题够了。~~

P1908 逆序对

首先注意到只有数字的大小关系重要，具体数字不重要，因此将数据离散化方便权值线段树处理。

从前往后把数据加入线段树。对于第

k

个数，前面的数对它产生的贡献为

\sum_{i=1}^{k-1}[a_i>a_k]

，那么

a_i

的范围为

[a_k+1,n]

（因为将数据离散化过）。使用权值线段树快速查即可，复杂度

\Theta(n\log n)

。

这个题用权值树状数组也行，不过更多题只能用线段树做。

代码是我远古时期写的，过于丑陋，不放了。

线段树二分

评价

难度： $5$
实用程度： $5$

介绍

一句话：把外部二分、内部线段树改为在线段树上二分。

如果你在外面做一次二分，在二分的 check() 中使用线段树查询，则会导致两只

\log

的复杂度。而如果选择在线段树查询过程中通过记录信息，决策向左子树还是右子树递归，则可以砍掉一只

\log

。这在许多题中是非常重要的。

例题

P5579 Siano

观察此题的性质：长得快得一定长得高，不管有没有被割掉，在将生长速度排序以后，每一次割掉的一定是一个后缀区间。

于是可以用线段树维护了：为了找到生长速度最小的被割的点，在线段树上额外记录包含区间的

\max

值，在递归时决定往左子树走还是右子树走。复杂度

\Theta(n\log n)

。

代码：

CPP

// NOTE: "[EDIT]" means you should edit this part by yourself
#include <bits/stdc++.h>
// [EDIT] please enable this line if there are many tests
//#define MULTITEST
using namespace std;
// [EDIT] if you want to copy some templates, please paste them here

typedef long long ll;
#define int ll
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define rep3(i,x,y,z) for (int i = (x);i <= (y);i += (z))
#define rep4(i,x,y,z) for (int i = (x);i >= (y);i -= (z))
#define cl(a) memset(a,0,sizeof(a))
// [EDIT] define some constants here
const int N = 5e5 + 10;
// [EDIT] define some variables, arrays, etc here
int n,q,d,b;
int a[N],sum[N];
struct node
{
	int height;
	int tim;
	int sum;
	int mx;
} t[N << 2];
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
inline void push_up(int p)
{
	t[p].sum = t[ls(p)].sum + t[rs(p)].sum;
	t[p].mx = t[rs(p)].mx;
}
inline void cut(int p,int l,int r,int v)
{
	t[p].height = v;
	t[p].tim = 0;
	t[p].sum = (r - l + 1) * v;
	t[p].mx = v;
}
inline void grow(int p,int l,int r,int v)
{
	t[p].tim += v;
	t[p].sum += (sum[r] - sum[l - 1]) * v;
	t[p].mx += a[r] * v;
}
void push_down(int p,int l,int r)
{
	int mid = (l + r) >> 1;
	if (t[p].height != -1)
	{
		cut(ls(p),l,mid,t[p].height);
		cut(rs(p),mid + 1,r,t[p].height);
		t[p].height = -1;
	}
	if (t[p].tim > 0)
	{
		grow(ls(p),l,mid,t[p].tim);
		grow(rs(p),mid + 1,r,t[p].tim);
		t[p].tim = 0;
	}
}
void build(int p,int l,int r)
{
	t[p].height = -1;
	if (l == r)
		return;
	int mid = (l + r) >> 1;
	build(ls(p),l,mid);
	build(rs(p),mid + 1,r);
}
int modify(int p,int l,int r,int L,int R,int v)
{
	if (L <= l && r <= R)
	{
		int tmp = t[p].sum;
		cut(p,l,r,v);
		return tmp - t[p].sum;
	}
	int ans = 0;
	int mid = (l + r) >> 1;
	push_down(p,l,r);
	if (L <= mid)
		ans += modify(ls(p),l,mid,L,R,v);
	if (R > mid)
		ans += modify(rs(p),mid + 1,r,L,R,v);
	push_up(p);
	return ans;
}
int query(int p,int l,int r,int v)
{
	if (l == r)
	{
		if (t[p].sum >= v)
			return l;
		else
			return n + 1;
	}
	int mid = (l + r) >> 1;
	push_down(p,l,r);
	if (t[ls(p)].mx >= v)
		return query(ls(p),l,mid,v);
	else
		return query(rs(p),mid + 1,r,v);
}
// [EDIT] a function to solve the problem
void solve()
{
    //input
	cin >> n >> q;
	rep1(i,1,n)
		cin >> a[i];
    //solve
    sort(a + 1,a + n + 1);
    rep1(i,1,n)
    	sum[i] = sum[i - 1] + a[i];
    build(1,1,n);
    int pre = 0;
	while (q--)
	{
		cin >> d >> b;
		grow(1,1,n,d - pre);
		pre = d;
		cout << modify(1,1,n,query(1,1,n,b),n,b) << '\n';
	}
    //output

    //clear

}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
#ifdef MULTITEST
    cin >> t;
#else
    t = 1;
#endif
    while (t--)
        solve();
}

P11833 [省选联考 2025] 推箱子

新鲜出炉的省选题，在我的另一篇学习笔记中也有提及。

结论：按照

t_i

从小到大贪心处理，中间遇上箱子就推着一起走。因为

a_i,b_i

均单调递增可以证明。

注意到推着一起走相当于把所有箱子都推到终点（相邻两个箱子之前相差

1

），是推平成等差数列操作。

这里有一个常见 trick：令

c_i=a_i-i

，则推平成等差数列转化为推平成一段相同的数。

在那篇笔记中我采用了珂朵莉树实现，但线段树显然也是可以的。记录一个区间的

\max,\min,\operatorname{sum}

线段树二分即可。

代码：

CPP

// NOTE: "[EDIT]" means you should edit this part by yourself
#include <bits/stdc++.h>
// [EDIT] please enable this line if there are many tests
#define MULTITEST
using namespace std;
// [EDIT] if you want to copy some templates, please paste them here

typedef long long ll;
#define int ll
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define rep3(i,x,y,z) for (int i = (x);i <= (y);i += (z))
#define rep4(i,x,y,z) for (int i = (x);i >= (y);i -= (z))
#define cl(a) memset(a,0,sizeof(a))
// [EDIT] define some constants here
const int N = 2e5 + 10;
// [EDIT] define some variables, arrays, etc here
int n;
struct xxx
{
	int a;
	int b;
	int t;
	int id;
	bool operator<(const xxx& xx) { return t < xx.t; }
} a[N];
struct segtree
{
	struct node
	{
		int l;
		int r;
		int sum;
		int mx;
		int mn;
		int lazy;
	} t[N << 2];
	inline int ls(int p) { return p << 1; }
	inline int rs(int p) { return p << 1 | 1; }
	inline void push_up(int p)
	{
		t[p].sum = t[ls(p)].sum + t[rs(p)].sum;
		t[p].mx = max(t[ls(p)].mx,t[rs(p)].mx);
		t[p].mn = min(t[ls(p)].mn,t[rs(p)].mn);
	}
	inline void modifyy(int p,int k,int len)
	{
		t[p].mx = k;
		t[p].mn = k;
		t[p].lazy = k;
		t[p].sum = k * len;
	}
	void push_down(int p)
	{
		if (t[p].lazy != -1)
		{
			int mid = (t[p].l + t[p].r) >> 1;
			modifyy(ls(p),t[p].lazy,mid - t[p].l + 1);
			modifyy(rs(p),t[p].lazy,t[p].r - mid);
			t[p].lazy = -1;
		}
	}
	void clear() { cl(t); }
	void build(int p,int l,int r)
	{
		t[p].l = l;
		t[p].r = r;
		t[p].lazy = -1;
		if (l == r)
		{
			t[p].sum = a[l].a;
			t[p].mx = a[l].a;
			t[p].mn = a[l].a;
			return;
		}
		int mid = (l + r) >> 1;
		build(ls(p),l,mid);
		build(rs(p),mid + 1,r);
		push_up(p);
	}
	void modify(int p,int l,int r,int k)
	{
		if (l <= t[p].l && t[p].r <= r)
		{
			modifyy(p,k,t[p].r - t[p].l + 1);
			return;
		}
		int mid = (t[p].l + t[p].r) >> 1;
		push_down(p);
		if (l <= mid)
			modify(ls(p),l,r,k);
		if (r > mid)
			modify(rs(p),l,r,k);
		push_up(p);
	}
	int query1(int p,int l,int r)
	{
		if (l <= t[p].l && t[p].r <= r)
			return t[p].sum;
		int mid = (t[p].l + t[p].r) >> 1;
		push_down(p);
		int ans = 0;
		if (l <= mid)
			ans += query1(ls(p),l,r);
		if (r > mid)
			ans += query1(rs(p),l,r);
		return ans;
	}
	int query2(int p,int k)
	{
		if (t[p].l == t[p].r)
			return t[p].l;
		int mid = (t[p].l + t[p].r) >> 1;
		push_down(p);
		if (t[rs(p)].mn <= k)
			return query2(rs(p),k);
		else
			return query2(ls(p),k);
	}
	int query3(int p,int k)
	{
		if (t[p].l == t[p].r)
			return t[p].l;
		int mid = (t[p].l + t[p].r) >> 1;
		push_down(p);
		if (t[ls(p)].mx >= k)
			return query3(ls(p),k);
		else
			return query3(rs(p),k);
	}
} t;
// [EDIT] a function to solve the problem
void solve()
{
    //input
	cin >> n;
	rep1(i,1,n)
	{
		a[i].id = i;
		cin >> a[i].a >> a[i].b >> a[i].t;
		a[i].a -= i;
		a[i].b -= i;
	}
    //solve
    t.clear();
	t.build(1,1,n);
	sort(a + 1,a + n + 1);
	int now = 0;
	rep1(i,1,n)
		if (a[i].a < a[i].b)
		{
			int pos = t.query2(1,a[i].b);
			now += a[i].b * (pos - a[i].id + 1) - t.query1(1,a[i].id,pos);
			if (now > a[i].t)
			{
				cout << "No\n";
				return;
			}
			t.modify(1,a[i].id,pos,a[i].b);
		}
		else
		{
			int pos = t.query3(1,a[i].b);
			now += t.query1(1,pos,a[i].id) - a[i].b * (a[i].id - pos + 1);
			if (now > a[i].t)
			{
				cout << "No\n";
				return;
			}
			t.modify(1,pos,a[i].id,a[i].b);
		}
    //output
	cout << "Yes\n";
    //clear

}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
#ifdef MULTITEST
    cin >> t >> t;
#else
    t = 1;
#endif
    while (t--)
        solve();
}

~~线段树跑不过珂朵莉树，怎么会事呢？~~

动态开点线段树

评价

难度： $4$
实用程度： $0/10$ （如果不需要用可持久化线段树之类高级东西则几乎为 $0$ ，否则必须用）

介绍

主要是可持久化线段树等的前置知识。

普通线段树需要长为

4n

的数组，

x

的左右儿子为

x\times 2,x\times 2+1

。而动态开点线段树只在必要的时候创建节点，左右儿子改为用 $ls,rs$ 动态记录。其余写法跟普通线段树没区别。

具体实现参见 OI-Wiki。

例题

动态开点线段树是一种优化技巧，不是特定算法，因此没有例题。

可持久化线段树

评价

难度： $7$
实用程度： $3$

介绍

在许多问题中，我们在对线段树进行修改的同时，还要支持查询历史版本。

最暴力的想法是每次开一颗线段树，但这空间显然是会爆掉的。

观察线段树结构，发现一次修改所涉及的节点最多只有

\Theta(\log n)

个，见下图（由于作者太懒，取自 OI-Wiki）：

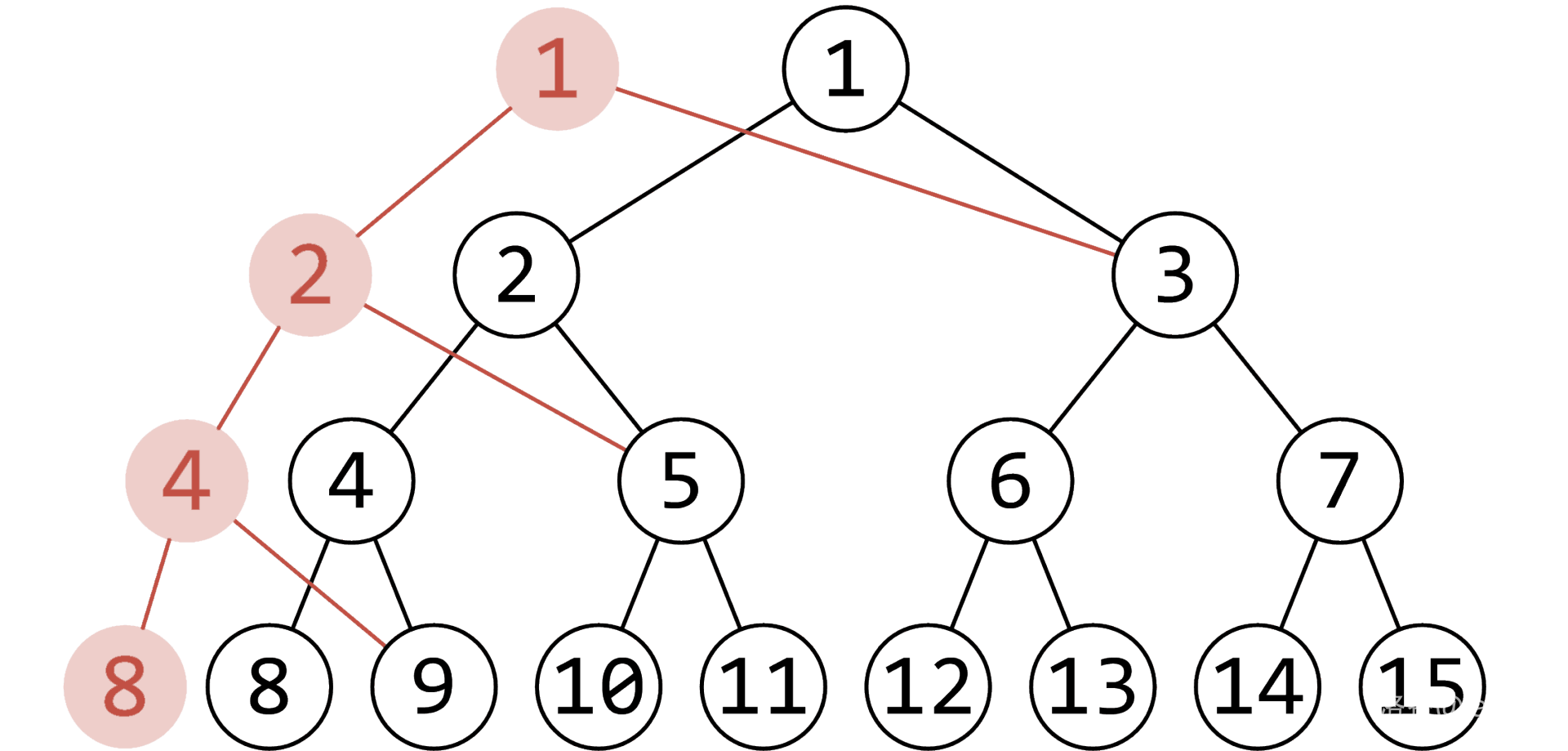
在上面这个例子中，我们对

1

号节点进行修改，只会更改红色节点。每层只有一个，而树高为

\log n

，因此只涉及到

\Theta(\log n)

个节点。

因此我们只要在每次修改时新开一棵线段树的一小部分即可。

例题

SP3946 MKTHNUM - K-th Number

非常经典的主席树题。

首先澄清一下许多人的误解，主席树是权值版本的可持久化线段树，并不等同于可持久化线段树，更准确地说是可持久化线段树的真子集。

考虑从前往后每次加入序列中的下一个元素，并生成一棵新的权值线段树。

运用前缀和的思想，区间

[l,r]

的答案就是用第

r

个版本的线段树减去第

l-1

个版本的线段树。因此主席树可以高效实现。

代码：

CPP

// NOTE: "[EDIT]" means you should edit this part by yourself
#include <bits/stdc++.h>
// [EDIT] please enable this line if there are many tests
//#define MULTITEST
using namespace std;
// [EDIT] if you want to copy some templates, please paste them here

typedef long long ll;
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define rep3(i,x,y,z) for (int i = (x);i <= (y);i += (z))
#define rep4(i,x,y,z) for (int i = (x);i >= (y);i -= (z))
#define cl(a) memset(a,0,sizeof(a))
// [EDIT] define some constants here
const int N = 1e5 + 10;
// [EDIT] define some variables, arrays, etc here
int n,q,ii,jj,kk,cnt;
int a[N],b[N];
struct node
{
	int sum;
	int root;
	int ls;
	int rs;
} t[N << 5];
void build(int& k,int l,int r)
{
	k = ++cnt;
	if (l == r)
		return;
	int mid = (l + r) >> 1;
	build(t[k].ls,l,mid);
	build(t[k].rs,mid + 1,r);
}
int modify(int p,int l,int r,int x)
{
	int xx = ++cnt;
	t[xx].ls = t[p].ls;
	t[xx].rs = t[p].rs;
	t[xx].sum = t[p].sum + 1;
	if (l == r)
		return xx;
	int mid = (l + r) >> 1;
	if (x <= mid)
		t[xx].ls = modify(t[xx].ls,l,mid,x);
	else
		t[xx].rs = modify(t[xx].rs,mid + 1,r,x);
	return xx;
}
int query(int u,int v,int l,int r,int k)
{
	int mid = (l + r) >> 1;
	int x = t[t[v].ls].sum - t[t[u].ls].sum;
	if (l == r)
		return l;
	if (x >= k)
		return query(t[u].ls,t[v].ls,l,mid,k);
	else
		return query(t[u].rs,t[v].rs,mid + 1,r,k - x);
}
// [EDIT] a function to solve the problem
void solve()
{
    //input
	cin >> n >> q;
	rep1(i,1,n)
	{
		cin >> a[i];
		b[i] = a[i];
	}
    //solve
	sort(b + 1,b + n + 1);
	int len = unique(b + 1,b + n + 1) - b - 1;
	build(t[0].root,1,len);
	rep1(i,1,n)
		t[i].root = modify(t[i - 1].root,1,len,lower_bound(b + 1,b + len + 1,a[i]) - b);
	while (q--)
	{
		cin >> ii >> jj >> kk;
		cout << b[query(t[ii - 1].root,t[jj].root,1,len,kk)] << '\n';
	}
    //output

    //clear

}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
#ifdef MULTITEST
    cin >> t;
#else
    t = 1;
#endif
    while (t--)
        solve();
}

P3402 可持久化并查集

可持久化并查集是基于可持久化线段树实现的。

把普通并查集的 fa 和 dep 数组扔到可持久化线段树上维护。

每次修改新建两个版本，一个更新 fa，一个更新 dep。要开两个版本的具体理由详见某巨佬的博客。

在可持久化并查集中路径压缩会被卡。只能用启发式合并。

代码：

CPP

// NOTE: "[EDIT]" means you should edit this part by yourself
#include <bits/stdc++.h>
// [EDIT] please enable this line if there are many tests
//#define MULTITEST
using namespace std;
// [EDIT] if you want to copy some templates, please paste them here

typedef long long ll;
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define rep3(i,x,y,z) for (int i = (x);i <= (y);i += (z))
#define rep4(i,x,y,z) for (int i = (x);i >= (y);i -= (z))
#define cl(a) memset(a,0,sizeof(a))
// [EDIT] define some constants here
const int N = 3e5 + 10;
// [EDIT] define some variables, arrays, etc here
int n,m,now,to,cnt,op,aa,bb;
int root[N];
struct node
{
	int ls;
	int rs;
	int fa;
	int dep;
} t[N * 20];
int build(int l,int r)
{
	int tt = ++cnt;
	if (l == r)
	{
		t[tt].fa = l;
		return tt;
	}
	int mid = (l + r) >> 1;
	t[tt].ls = build(l,mid);
	t[tt].rs = build(mid + 1,r);
	return tt;
}
int query(int nw,int l,int r,int x)
{
	if (l == r)
		return nw;
	int mid = (l + r) >> 1;
	if (x <= mid)
		return query(t[nw].ls,l,mid,x);
	else
		return query(t[nw].rs,mid + 1,r,x);
}
int find(int nw,int a)
{
	int ff = query(root[nw],1,n,a);
	if (t[ff].fa == a)
		return ff;
	return find(nw,t[ff].fa);
}
int newnode(int nw)
{
	int tt = ++cnt;
	t[tt] = t[nw];
	return tt;
}
int hb(int nw,int l,int r,int x,int f)
{
	int tt = newnode(nw);
	if (l == r)
	{
		t[tt].fa = f;
		return tt;
	}
	int mid = (l + r) >> 1;
	if (x <= mid)
		t[tt].ls = hb(t[nw].ls,l,mid,x,f);
	else
		t[tt].rs = hb(t[nw].rs,mid + 1,r,x,f);
	return tt;
}
int add(int nw,int l,int r,int x)
{
	int tt = newnode(nw);
	if (l == r)
	{
		t[tt].dep++;
		return tt;
	}
	int mid = (l + r) >> 1;
	if (x <= mid)
		t[tt].ls = add(t[nw].ls,l,mid,x);
	else
		t[tt].rs = add(t[nw].rs,mid + 1,r,x);
	return tt;
}
void merge(int nw,int a,int b)
{
	root[nw] = root[nw - 1];
	a = find(nw,a);
	b = find(nw,b);
	if (t[a].fa != t[b].fa)
	{
		if (t[a].dep > t[b].dep)
			swap(a,b);
		root[nw] = hb(root[nw - 1],1,n,t[a].fa,t[b].fa);
		if (t[a].dep == t[b].dep)
			root[nw] = add(root[nw],1,n,t[b].fa);
	}
}
bool check(int nw,int a,int b)
{
	a = find(nw,a);
	b = find(nw,b);
	return t[a].fa == t[b].fa;
}
// [EDIT] a function to solve the problem
void solve()
{
    //input
	cin >> n >> m;
    //solve
	root[0] = build(1,n);
	rep1(i,1,m)
	{
		cin >> op >> aa;
		switch (op)
		{
			case 1:
				cin >> bb;
				merge(i,aa,bb);
				break;
			case 2:
				root[i] = root[aa];
				break;
			case 3:
				cin >> bb;
				cout << check(i - 1,aa,bb) << '\n';
				root[i] = root[i - 1];
				break;
		}
	}
    //output

    //clear

}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
#ifdef MULTITEST
    cin >> t;
#else
    t = 1;
#endif
    while (t--)
        solve();
}

扫描线

评价

难度： $7$
实用程度： $3$

介绍

扫描线是数据结构与几何结合的一个经典案例（？，但实用程度不高就是了。

它的核心思想是维护一个从下到上（其他方向也没关系）扫的扫描线，分析图形被截得的线段长。

具体见下方模板题例题的解析。

例题

P5490 【模板】扫描线 & 矩形面积并

都是矩形的条件将这题简化了很多。~~运用微积分求面积的思想~~，只要对于每个

x

，将其截得长度累加即可。

每次扫描线在遇到横边时停下来。为了快速计算，将图形上横边赋值为 $-1$ ，下横边权值为 $1$ 。这一点需要仔细体会。可以简单地理解为上下相减才能求出面积。

最后将所有点

x

坐标离散化缩小范围。用线段树，每次向上扫描后更新就行了。

代码：

CPP

#include <bits/stdc++.h>
#define int long long
#define y1 JiNianCSPJ_2024T2BaWoChuangSiDeTiMuWoYiHouZaiYeBuHuiFanZheGeCuoLeQAQ
#define rep1(i,a,b) for (int i = (a);i <= (b);i++)
using namespace std;
const int N = 2e6 + 10;
int n,x1,y1,x2,y2,ans;
int x[N];
struct xxx
{
	int l;
	int r;
	int h;
	int mark;
} line[N];
struct node
{
	int l;
	int r;
	int sum;
	int len;
} t[N];
bool cmp(const xxx& xx,const xxx& yy) { return xx.h < yy.h; }
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
void build(int p,int l,int r)
{
	t[p].l = l;
	t[p].r = r;
	if (l == r)
		return;
	int mid = (l + r) >> 1;
	build(ls(p),l,mid);
	build(rs(p),mid + 1,r);
}
inline void push_up(int p)
{
	if (t[p].sum != 0)
		t[p].len = x[t[p].r + 1] - x[t[p].l];
	else
		t[p].len = t[ls(p)].len + t[rs(p)].len;
}
void modify(int p,int l,int r,int k)
{
	if (x[t[p].r + 1] <= l || r <= x[t[p].l])
		return;
	if (l <= x[t[p].l] && x[t[p].r + 1] <= r)
		t[p].sum += k;
	else
	{
		modify(ls(p),l,r,k);
		modify(rs(p),l,r,k);
	}
	push_up(p);
}
signed main()
{
	cin >> n;
	rep1(i,1,n)
	{
		cin >> x1 >> y1 >> x2 >> y2;
		x[2 * i - 1] = x1;
		x[2 * i] = x2;
		line[2 * i - 1] = {x1,x2,y1,1};
		line[2 * i] = {x1,x2,y2,-1};
	}
	n *= 2;
	sort(line + 1,line + n + 1,cmp);
	sort(x + 1,x + n + 1);
	int len = unique(x + 1,x + n + 1) - x - 1;
	build(1,1,len - 1);
	rep1(i,1,n - 1)
	{
		modify(1,line[i].l,line[i].r,line[i].mark);
		ans += t[1].len * (line[i + 1].h - line[i].h);
	}
	cout << ans;
}

~~可以细读一下代码第三行。~~

AT_abc346_g [ABC346G] Alone

枚举要求的区间中的唯一整数。对于元素

a_i

，如果它在

[l,r]

区间中只出现一次，则

a_l\cdots a_{i-1},a_{i+1}\cdots a_r

都不与

a_i

相同。每个元素的

l,r

可以用 map 求。则方案数为

(i-l+1)\times(r-i+1)

。

但这样会重复统计。观察到就是求多个左下角

(l_i,i)

，右上角

(i,r_i)

的矩形面积并。扫描线即可。

代码：

CPP

#include <bits/stdc++.h>
#define int long long
#define y1 JiNianCSPJ_2024T2BaWoChuangSiDeTiMuWoYiHouZaiYeBuHuiFanZheGeCuoLeQAQ
#define rep1(i,a,b) for (int i = (a);i <= (b);i++)
#define rep2(i,a,b) for (int i = (a);i >= (b);i--)
using namespace std;
const int N = 2e6 + 10;
int n,x1,y1,x2,y2,ans;
int x[N],a[N],p[N],l[N],r[N];
struct xxx
{
	int l;
	int r;
	int h;
	int mark;
} line[N];
struct node
{
	int l;
	int r;
	int sum;
	int len;
} t[N];
bool cmp(const xxx& xx,const xxx& yy) { return xx.h < yy.h; }
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
void build(int p,int l,int r)
{
	t[p].l = l;
	t[p].r = r;
	if (l == r)
		return;
	int mid = (l + r) >> 1;
	build(ls(p),l,mid);
	build(rs(p),mid + 1,r);
}
inline void push_up(int p)
{
	if (t[p].sum != 0)
		t[p].len = x[t[p].r + 1] - x[t[p].l];
	else
		t[p].len = t[ls(p)].len + t[rs(p)].len;
}
void modify(int p,int l,int r,int k)
{
	if (x[t[p].r + 1] <= l || r <= x[t[p].l])
		return;
	if (l <= x[t[p].l] && x[t[p].r + 1] <= r)
		t[p].sum += k;
	else
	{
		modify(ls(p),l,r,k);
		modify(rs(p),l,r,k);
	}
	push_up(p);
}
signed main()
{
	cin >> n;
	rep1(i,1,n)
		cin >> a[i];
	rep1(i,1,n)
	{
		l[i] = p[a[i]];
		p[a[i]] = i;
	}
	rep1(i,1,n)
		p[i] = n + 1;
	rep2(i,n,1)
	{
		r[i] = p[a[i]];
		p[a[i]] = i;
	}
	rep1(i,1,n)
	{
		x1 = l[i];
		y1 = i;
		x2 = i;
		y2 = r[i];
		x[2 * i - 1] = x1;
		x[2 * i] = x2;
		line[2 * i - 1] = {x1,x2,y1,1};
		line[2 * i] = {x1,x2,y2,-1};
	}
	n *= 2;
	sort(line + 1,line + n + 1,cmp);
	sort(x + 1,x + n + 1);
	int len = unique(x + 1,x + n + 1) - x - 1;
	build(1,1,len - 1);
	rep1(i,1,n - 1)
	{
		modify(1,line[i].l,line[i].r,line[i].mark);
		ans += t[1].len * (line[i + 1].h - line[i].h);
	}
	cout << ans;
}

线段树分治

评价

难度： $7$
实用程度： $4$

介绍

线段树分治适用于离线解决“某元素（可能是边）在某时刻出现、某时消失”的问题。

核心思想是离线后在时间轴上建线段树。对于每个操作，相当于在线段树上进行区间修改/查询。

其最重要的作用是，辅助一些撤销操作复杂度不优秀的数据结构使用。

例题

P5787 二分图 /【模板】线段树分治

引理：一个图是二分图等价于该图不存在奇环。~~读者自证不难。~~

奇环就可以用扩展域并查集快速维护了。黑白染色，

0/1

分别表示两种颜色，相撞了就是奇环。

然后线段树分治搞搞即可。为了支持回溯操作，要用可撤销并查集。

代码：

CPP

// NOTE: "[EDIT]" means you should edit this part by yourself
#include <bits/stdc++.h>
// [EDIT] please enable this line if there are many tests
//#define MULTITEST
using namespace std;
// [EDIT] if you want to copy some templates, please paste them here

typedef long long ll;
typedef pair<int,int> pii;
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define rep3(i,x,y,z) for (int i = (x);i <= (y);i += (z))
#define rep4(i,x,y,z) for (int i = (x);i >= (y);i -= (z))
#define cl(a) memset(a,0,sizeof(a))
// [EDIT] define some constants here
const int N = 2e5 + 10;
const int M = 1e5 + 3;
// [EDIT] define some variables, arrays, etc here
int n,m,k,l,r;
int fa[N],d[N],u[N],v[N];
struct node
{
	int l;
	int r;
	vector<int> v;
} t[N << 2];
stack<pii> st;
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
void build(int p,int l,int r)
{
	t[p].l = l;
	t[p].r = r;
	if (l == r)
		return;
	int mid = (l + r) >> 1;
	build(ls(p),l,mid);
	build(rs(p),mid + 1,r);
}
void insert(int p,int l,int r,int x)
{
	if (l <= t[p].l && t[p].r <= r)
	{
		t[p].v.push_back(x);
		return;
	}
	int mid = (t[p].l + t[p].r) >> 1;
	if (l <= mid)
		insert(ls(p),l,r,x);
	if (r > mid)
		insert(rs(p),l,r,x);
}
int find(int x)
{
	if (fa[x] == x)
		return x;
	return find(fa[x]);
}
void merge(int x,int y)
{
	if (x == y)
		return;
	if (d[x] > d[y])
		swap(x,y);
	if (d[x] == d[y])
	{
		st.push({x,1});
		fa[x] = y;
		d[y]++;
	}
	else
	{
		st.push({x,0});
		fa[x] = y;
	}
}
void undo()
{
	d[fa[st.top().first]] -= st.top().second;
	fa[st.top().first] = st.top().first;
	st.pop(); 
}
void dfs(int p,int l,int r)
{
	bool flag = true;
	int sz = st.size();
	for (auto p : t[p].v)
	{
		int uu = find(u[p]);
		int vv = find(v[p]);
		if (uu == vv)
		{
			rep1(j,l,r)
				cout << "No\n";
			flag = false;
			break;
		}
		merge(find(u[p] + M),vv);
		merge(find(v[p] + M),uu);
	}
	if (flag)
	{
		if (l == r)
			cout << "Yes\n";
		else
		{
			int mid = (t[p].l + t[p].r) >> 1;
			dfs(ls(p),l,mid);
			dfs(rs(p),mid + 1,r);
		}
	}
	while (st.size() > sz)
		undo();
}
// [EDIT] a function to solve the problem
void solve()
{
    //input
	cin >> n >> m >> k;
	build(1,1,k);
	rep1(i,1,m)
	{
		cin >> u[i] >> v[i] >> l >> r;
		if (l != r)
			insert(1,l + 1,r,i);
	}
    //solve
	rep1(i,1,n)
	{
		fa[i] = i;
		fa[i + M] = i + M;
	}
	dfs(1,1,k);
    //output

    //clear

}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
#ifdef MULTITEST
    cin >> t;
#else
    t = 1;
#endif
    while (t--)
        solve();
}

树链剖分

评价

难度： $8$
实用程度： $5$

介绍

其实严格来说树链剖分与线段树并无直接关系，但由于树剖的内部数据结构大多数时候是线段树，故也将其加入线段树文章中。

树链剖分，简称树剖，将一棵树划分成多条链，并使用数据结构快速维护。

树剖有多种形式，包括重链剖分、长链剖分等，其中最常见的是重链剖分（也被称为轻重链剖分，本质一样）。

首先给出一组定义：

定义重子节点表示其子节点中子树最大的子结点之一。如果没有子节点，就无重子节点。
定义轻子节点表示该节点剩余的其他子结点。
从这个结点到重子节点的边为重边。
从这个结点到轻子节点的边为轻边。
若干条首尾衔接的重边构成重链。

由于作者太懒，再次用 OI-Wiki 的图：

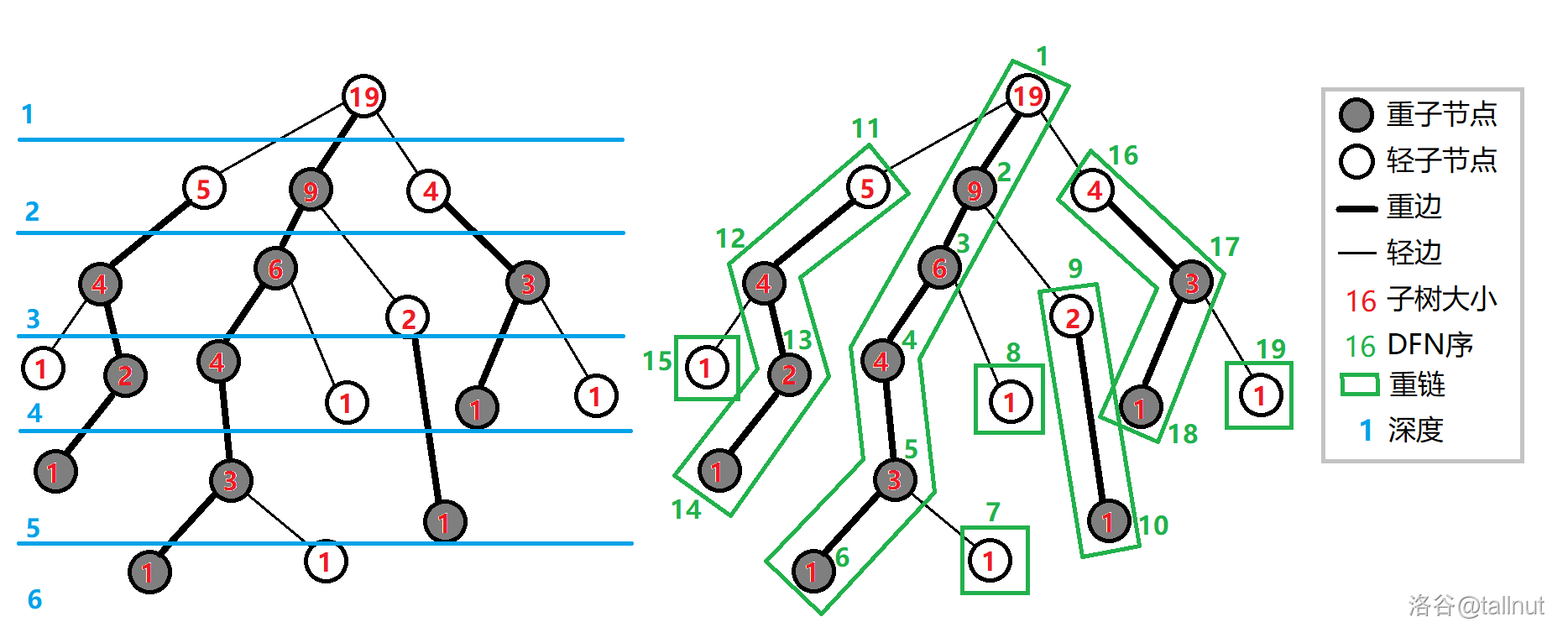
预处理部分：预处理所有节点的父亲 fa、深度 dep、其子树大小 siz、重子节点 son、DFS 序 dfn、该节点所在重链的顶部 top，以及所有 DFS 序对应的节点编号（即 dfn 的反函数，因为 dfn 是单射）。这些都可以用两遍 DFS 求出来。

可以发现，每向下走一条轻边，子树大小至少减半。因此树剖本身一次操作的时间复杂度为

\Theta(\log n)

，当然这不算线段树等内部数据结构带来的

\log

。

例题

P3384 【模板】重链剖分/树链剖分

模板题。考虑四个操作怎么做：

操作 $1$ ：每次选择两个点的 top 中深度较大的往上跳，这条链用线段树快速加。复杂度两只 $\log$ 。
操作 $2$ ：与操作 $1$ 类似，将修改换成查询即可。
操作 $3$ ：观察到一个子树内 DFS 序必定连续。于是线段树修改即可，复杂度一只 $\log$ 。
操作 $4$ ：类似操作 $3$ 。

代码：

CPP

#include <bits/stdc++.h>
using namespace std;
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
//CONSTANTS,VARIABLES
const int N = 1e5 + 10;
int n,q,r,mod,op,x,y,z,cnt;
int w[N],dep[N],siz[N],son[N],fa[N],top[N],dfn[N],wn[N];
vector<int> graph[N];
//树剖预处理DFS
void dfs1(int p,int faa)
{
    dep[p] = dep[faa] + 1;
    siz[p] = 1;
    fa[p] = faa;
    for (auto j : graph[p])
        if (j != faa)
        {
            dfs1(j,p);
            siz[p] += siz[j];
            if (siz[j] > siz[son[p]])
                son[p] = j;
        }
}
void dfs2(int p,int faa)
{
    if (p == son[faa])
        top[p] = top[faa];
    else
        top[p] = p;
    dfn[p] = ++cnt;
    wn[cnt] = w[p];
    if (son[p] == 0)
        return;
    dfs2(son[p],p);
    for (auto j : graph[p])
        if (j != faa && j != son[p])
            dfs2(j,p);
}
//SEGTREE
struct node
{
    int l;
    int r;
    int x;
    int lazy;
} t[N << 2];
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
inline void push_up(int p) { t[p].x = (t[ls(p)].x + t[rs(p)].x) % mod; }
void push_down(int p)
{
    t[ls(p)].lazy += t[p].lazy;
    t[rs(p)].lazy += t[p].lazy;
    t[ls(p)].x = (t[ls(p)].x + 1ll * t[p].lazy * (t[ls(p)].r - t[ls(p)].l + 1)) % mod;
    t[rs(p)].x = (t[rs(p)].x + 1ll * t[p].lazy * (t[rs(p)].r - t[rs(p)].l + 1)) % mod;
    t[p].lazy = 0;
}
void build(int p,int l,int r)
{
    t[p].l = l;
    t[p].r = r;
    if (l == r)
    {
        t[p].x = wn[l] % mod;
        return;
    }
    int mid = (l + r) >> 1;
    build(ls(p),l,mid);
    build(rs(p),mid + 1,r);
    push_up(p);
}
void modify(int p,int l,int r,int k)
{
    if (l <= t[p].l && t[p].r <= r)
    {
        t[p].lazy += k;
        t[p].x += (t[p].r - t[p].l + 1) * k;
        return;
    }
    push_down(p);
    int mid = (t[p].l + t[p].r) >> 1;
    if (l <= mid)
        modify(ls(p),l,r,k);
    if (r > mid)
        modify(rs(p),l,r,k);
    push_up(p);
}
int query(int p,int l,int r)
{
    if (l <= t[p].l && t[p].r <= r)
        return t[p].x % mod;
    push_down(p);
    int mid = (t[p].l + t[p].r) >> 1;
    int ans = 0;
    if (l <= mid)
        ans = (ans + query(ls(p),l,r)) % mod;
    if (r > mid)
        ans = (ans + query(rs(p),l,r)) % mod;
    return ans;
}
//树剖操作
void modify1(int u,int v,int k)
{
    k %= mod;
    int ans = 0;
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])
            swap(u,v);
        modify(1,dfn[top[u]],dfn[u],k);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v])
        swap(u,v);
    modify(1,dfn[v],dfn[u],k);
}
int query1(int u,int v)
{
    int ans = 0;
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])
            swap(u,v);
        ans = (ans + query(1,dfn[top[u]],dfn[u])) % mod;
        u = fa[top[u]];
    }
    if (dep[u] < dep[v])
        swap(u,v);
    ans = (ans + query(1,dfn[v],dfn[u])) % mod;
    return ans;
}
void modify2(int p,int k) { modify(1,dfn[p],dfn[p] + siz[p] - 1,k % mod); }
int query2(int p) { return query(1,dfn[p],dfn[p] + siz[p] - 1); }
//MAIN
int main()
{
    cin >> n >> q >> r >> mod;
    rep1(i,1,n)
        cin >> w[i];
    rep1(i,1,n - 1)
    {
        cin >> x >> y;
        graph[x].push_back(y);
        graph[y].push_back(x);
    }
    dfs1(r,0);
    dfs2(r,0);
    build(1,1,n);
    while (q--)
    {
        cin >> op >> x;
        switch (op)
        {
            case 1:
                cin >> y >> z;
                modify1(x,y,z);
                break;
            case 2:
                cin >> y;
                cout << query1(x,y) << '\n';
                break;
            case 3:
                cin >> y;
                modify2(x,y);
                break;
            case 4:
                cout << query2(x) << '\n';
                break;
        }
    }
}

P3979 遥远的国度

感谢 @zhikang 教会我代码实现细节，orz。

一开始按照

1

为根 DFS。

前两个操作是树剖板子，用区间覆盖、区间查

\min

即可。

第三种需要分类讨论。设换成的根为

x

，原树根为

rt

：

如果 $rt=x$ ：显然是对 $[1,n]$ 整棵树进行查询。
否则，令 $l=\operatorname{LCA}(rt,x)$ $l = LCA (r t, x)$ ：
- $l=x$ ：查询的就是这棵子树本身；
- 否则，在整棵树中抠掉这棵子树，对剩余部分进行查询。

以上内容画个图很好理解。

代码：

CPP

#include <bits/stdc++.h>
#define rep1(i,x,y) for (int i = (x);i <= (y);i++)
#define rep2(i,x,y) for (int i = (x);i >= (y);i--)
#define int long long
using namespace std;
const int N = 2e5 + 10;
int n,q,op,u,v,x,y,z,cnt,rt;
int a[N],siz[N],dep[N],son[N],top[N],dfn[N],rk[N],fa[N],ffa[20][N];
vector<int> graph[N];
#define mid ((t[p].l + t[p].r) >> 1)
class segtree
{
	struct node
	{
		int l;
		int r;
		int mn;
		int lazy;
	} t[N << 2];
	inline int ls(int p) { return p << 1; }
	inline int rs(int p) { return p << 1 | 1; }
	inline void push_up(int p) { t[p].mn = min(t[ls(p)].mn,t[rs(p)].mn); }
	void push_down(int p)
	{
		if (t[p].lazy)
		{
			t[ls(p)].mn = t[p].lazy;
			t[rs(p)].mn = t[p].lazy;
			t[ls(p)].lazy = t[p].lazy;
			t[rs(p)].lazy = t[p].lazy;
			t[p].lazy = 0;
		}
	}
	void build_p(int p,int l,int r,int a[])
	{
		t[p].l = l;
		t[p].r = r;
		if (l == r)
		{
			t[p].mn = a[rk[l]];
			return;
		}
		build_p(ls(p),l,mid,a);
		build_p(rs(p),mid + 1,r,a);
		push_up(p);
	}
	int query_p(int p,int l,int r)
	{
		if (l <= t[p].l && t[p].r <= r)
			return t[p].mn;
		push_down(p);
		int ans = 2e9;
		if (l <= mid)
			ans = min(ans,query_p(ls(p),l,r));
		if (r > mid)
			ans = min(ans,query_p(rs(p),l,r));
		return ans;
	}
	void modify_p(int p,int l,int r,int k)
	{
		if (l <= t[p].l && t[p].r <= r)
		{
			t[p].mn = k;
			t[p].lazy = k;
			return;
		}
		push_down(p);
		if (l <= mid)
			modify_p(ls(p),l,r,k);
		if (r > mid)
			modify_p(rs(p),l,r,k);
		push_up(p);
	}
	public:
		segtree() { memset(t,0,sizeof t); }
		void build(int n,int a[]) { build_p(1,1,n,a); }
		int query(int l,int r) { return query_p(1,l,r); }
		void modify(int l,int r,int k) { modify_p(1,l,r,k); }
} t;
#undef mid
void dfs1(int p,int faa)
{
	siz[p] = 1;
	fa[p] = faa;
	ffa[0][p] = faa;
	rep1(i,1,19)
		ffa[i][p] = ffa[i - 1][ffa[i - 1][p]];
	dep[p] = dep[faa] + 1;
	for (auto j : graph[p])
		if (j != faa)
		{
			dfs1(j,p);
			siz[p] += siz[j];
			if (siz[j] > siz[son[p]])
				son[p] = j;
		}
}
void dfs2(int p,int faa)
{
	if (p == son[faa])
		top[p] = top[faa];
	else
		top[p] = p;
	dfn[p] = ++cnt;
	rk[cnt] = p;
	if (son[p] == 0)
		return;
	dfs2(son[p],p);
	for (auto j : graph[p])
		if (j != faa && j != son[p])
			dfs2(j,p);
}
int jump(int p,int step)
{
	rep2(i,19,0)
		if ((1 << i) <= step)
		{
			p = ffa[i][p];
			step -= (1 << i);
		}
	return p;
}
int lca(int x,int y)
{
	while (top[x] != top[y])
	{
		if (dep[top[x]] > dep[top[y]])
			x = fa[top[x]];
		else
			y = fa[top[y]];
	}
	if (dep[x] < dep[y])
		return x;
	else
		return y;
}
void modify(int x,int y,int k)
{
	while (top[x] != top[y])
	{
		if (dep[top[x]] > dep[top[y]])
		{
			t.modify(dfn[top[x]],dfn[x],k);
			x = fa[top[x]];
		}
		else
		{
			t.modify(dfn[top[y]],dfn[y],k);
			y = fa[top[y]];
		}
	}
	if (dfn[x] < dfn[y])
		t.modify(dfn[x],dfn[y],k);
	else
		t.modify(dfn[y],dfn[x],k);
}
int qquery(int x)
{
	int lcaa = lca(x,rt);
	if (lcaa != x)
		return t.query(dfn[x],dfn[x] + siz[x] - 1);
	if (x != rt)
	{
		int tt = jump(rt,dep[rt] - dep[x] - 1);
		int ans1 = 2e9;
		int ans2 = 2e9;
		if (dfn[tt] > 1)
			ans1 = t.query(1,dfn[tt] - 1);
		if (dfn[tt] + siz[tt] <= n)
			ans2 = t.query(dfn[tt] + siz[tt],n);
		return min(ans1,ans2);
	}
	return t.query(1,n);
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> q;
	rep1(i,1,n - 1)
	{
		cin >> u >> v;
		graph[u].push_back(v);
		graph[v].push_back(u);
	}
	rep1(i,1,n)
		cin >> a[i];
	cin >> rt;
	dfs1(1,0);
	dfs2(1,0);
	t.build(n,a);
	while (q--)
	{
		cin >> op >> x;
		switch (op)
		{
			case 1:
				rt = x;
				break;
			case 2:
				cin >> y >> z;
				modify(x,y,z);
				break;
			case 3:
				cout << qquery(x) << '\n';
				break;
		}
	}
}