专栏文章

P14382 [JOISC 2017] 开荒者 / Cultivation

DDea_He
P14382题解参与者 4已保存评论 3

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
3 条
当前快照
1 份
快照标识符
@min9r4oz
此快照首次捕获于
2025/12/01 22:53
3 个月前
此快照最后确认于
2025/12/01 22:53
3 个月前
查看原文

题目大意

（根据个人习惯，将题目中的部分变量名做了修改）
有一个 N×MN \times M 的矩阵，除了有 KK 个位置为 11 以外全为 00，每次可以让所有为 11 的点克隆并向一个四联通的方向走一步。
问，将所有点变为 11 的最小操作次数。

解题思路

现在有一片矩形的草块，从 (x,y)(x,y) 覆盖到 (xx,yy)(xx,yy)，考虑一次风向对其的影响：
  • 向北，变为 (x−1,y)(x-1,y) 到 (xx,yy)(xx,yy)
  • 向南，变为 (x,y)(x,y) 到 (xx+1,yy)(xx+1,yy)
  • 向西，变为 (x,y−1)(x,y-1) 到 (xx,yy)(xx,yy)
  • 向东，变为 (x,y)(x,y) 到 (xx,yy+1)(xx,yy+1)
很容易发现，操作的顺序与最终的覆盖无关，也就是说，我们只需要找每个操作的次数就可以了。再随便优化一下，我们就有了一个 O(N2M2K)O(N^2M^2K) 的算法，拿下子任务1和2非常可观的15pts。
子任务3应该是很有启发性的，仍然可以 O(N2)O(N^2) 枚举一个 aa 和 bb，而另一维要么贪心，要么DP。从上往下扫行，我们现在还不确定列动的 cc 和 dd，但可以得到的是初始时，一些行已经占领的一些 11 点，形如很多竖直线（画得有点抽象）。
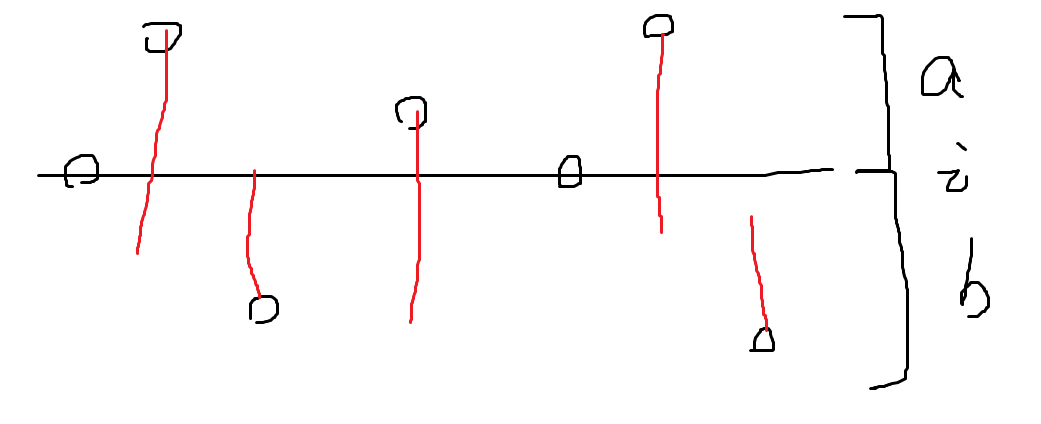
假设这些点的y坐标为序列 tt，且有 zz 个，那么我们的 cc 和 dd 要对所有行都满足 ti+d>ti+1−c(1≤i<z)t_i + d > t_{i+1} - c(1 \le i < z)，最左边和最右边要特判即 t1−c≤1∧tz+d≥Mt_1 - c \le 1 \land t_z + d \ge M。
要把 cc 和 dd 求出来是非常困难的，但我们只需要知道它俩的和就可以了，并且发现在第一个限制中左右的 cc 和 dd 是异号的，非常开心，整理一下得到 c+d≥max⁡(max⁡1≤i<zti+1−ti−1,t1−1+M−tz)c + d \ge \max(\max_{1 \le i < z} t_{i+1} - t_i - 1,t_1 - 1 + M - t_z)。复杂度 O(N2K)O(N^2K)，就可以得到30pts了！！！
但 NN 的范围依然非常大，并不能枚举，尽可能让复杂度往 KK 上靠。问题在于如何在不完全确定 aa 和 bb 的状态下，求出每行的 zz。
我们观察上面的图发现，这个时候 aa 加1，bb 减1后，只会对最后一行有影响，但其实我们可以直接把枚举 bb 的时间去掉，直接枚举 a+ba + b，然后看有 max⁡x−N\max x - N 到 max⁡x\max x 满足要求的最小 c+dc + d，感觉滑动窗口能写（这部分的具体实现放最后补充说明了，可以先去看看），复杂度 O(NK+K3)O(NK + K^3)，不知道为啥没这档分，是启发性不大还是太简单了。
现在还有一个 NN 需要优化，根据数据范围我们可以猜到，其实只有 K2K^2 个 a+ba + b 是备选答案。因为我们至少要满足每一行有一个 11 点，这样的限制与 c+dc + d 的限制是类似的，可以用相同的方法推出。现在就非常接近正解了！！！
实现上来看，我们枚举的 a+ba + b 其实就是要使 tt 序列不完全相同的，容易想到这样的 a+ba + b 只可能是 xi−xj−1x_i - x_j-1 或者 xi−1+R−xjx_i - 1 + R - x_j，复杂度 O(K3)O(K^3)。
补充说明：能覆盖到某一行的 11 点的 xx 一定是一段区间，所以可以 O(K3)O(K^3) 预处理出某一段点对应的三部分的贡献，即需要分别维护 max⁡1≤i<zti+1−ti−1\max_{1 \le i < z} t_{i+1} - t_i - 1，t1−1t_1 - 1，M−tzM - t_z，预处理时可以不用排序，扫描线加链表即可，我们就只需要对本质不同的每一行求出其点区间左端点和右端点，维护一个标号的最小值和最大值即可，对 xx 排序后双指针维护。
我的实现细节诡异的多，建议不要太参考。
附代码。
CPP
#include<bits/stdc++.h>
#define ll long long
#define LL __int128
#define pb push_back
#define fi first
#define se second
#define low(x,n,k) (int)(lower_bound(x+1,x+(n+1),k)-x)
#define upp(x,n,k) (int)(upper_bound(x+1,x+(n+1),k)-x)
using namespace std;
char BEGIN;
namespace hwq{
	inline int read(){int x=0;char ch=getchar();while(!isdigit(ch)) ch=getchar();while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-48,ch=getchar();return x;}
	const int MAXN=1e5+5;
	const int INF=2e9+5;
	int n,m,K;
	int nxt[MAXN],pre[MAXN],head; 
	ll f[305][305][3],mx[3][MAXN];
	struct node{
		int x,y;
		bool operator<(const node &a)const{return x<a.x;}; 
	}s[MAXN];
	struct deque{
		int que[MAXN],ql,qr,mx[MAXN],L[MAXN],R[MAXN];
		inline void clear(){ql=1,qr=0;}
		inline void Add(int l,const int &r,const int &x){
//			printf("Add(%d,%d,%d)\n",l,r,x);
			if(l>r) return ;
			while(ql<=qr&&mx[qr]<=x){
				if(R[qr]+1==l) l=L[qr];
				qr--;
			}
			mx[++qr]=x,L[qr]=l,R[qr]=r;
		}
		inline void Del(const int &x){while(ql<=qr&&R[ql]<=x) ql++;}
		inline ll front(){return mx[ql];}
		inline int gL(){return ql>qr?INF:L[ql];} 
		inline int gR(){return ql>qr?INF:R[ql];} 
	}q[3];
	int main(){
		n=read(),m=read(),K=read(); 
		for(int i=1;i<=K;i++) s[i].x=read(),s[i].y=read();
		sort(s+1,s+K+1);
		auto add=[&](const int &x){
			pre[x]=nxt[x]=0;
			if(!head||s[head].y>=s[x].y) return nxt[x]=head,pre[head]=x,head=x,void();
			int i=head;
			for(;nxt[i];i=nxt[i]) if(s[nxt[i]].y>=s[x].y) break;
			nxt[x]=nxt[i],pre[x]=i;
			if(nxt[i]) pre[nxt[i]]=x;
			nxt[i]=x;
		};
		for(int i=1;i<=K;i++){
			head=0;
			for(int j=i;j<=K;j++){
				add(j);
				int k=head;
				f[i][j][0]=s[head].y-1;
				for(;nxt[k];k=nxt[k]) f[i][j][1]=max(f[i][j][1],(ll)s[nxt[k]].y-s[k].y-1); 
				f[i][j][2]=m-s[k].y; 
			}
		}
		auto solve=[&](const int &len){
			if(len<0) return (ll)INF;
			ll ans=(ll)INF;
			for(int p=0;p<3;p++) q[p].clear();
			for(int i=1,j=1,pre=s[i].x-len;i<=K;i++){
				while(s[j].x<s[i].x-len){
					if(s[j].x==s[j-1].x){
						j++;
						continue;
					}
					for(int p=0;p<3;p++) q[p].Del(s[j].x-n);
					pre=max(pre,s[i-1].x-len);
					for(int p=0;p<3;p++) q[p].Add(pre,s[j].x,f[j][i-1][p]);
					pre=max(pre,s[j].x+1); 
					if(max({q[0].gL(),q[1].gL(),q[2].gL()})<=s[j].x-n+1) ans=min(ans,max(q[1].front(),q[0].front()+q[2].front()));
					j++; 
				}
				if(s[i].x==s[j].x||s[i].x==s[i-1].x) continue;
				for(int p=0;p<3;p++) q[p].Del(s[i].x-len-1-n);
				pre=max(pre,s[j].x-len);
				for(int p=0;p<3;p++) q[p].Add(pre,s[i].x-len-1,f[j][i-1][p]);
				pre=max(pre,s[i].x-len);
				if(max({q[0].gL(),q[1].gL(),q[2].gL()})<=s[i].x-len-1-n+1) ans=min(ans,max(q[1].front(),q[0].front()+q[2].front()));
			}
			return ans+len;
		};
		s[++K]=node{INF,0},s[0]=node{-INF,0};
		ll ans=solve(0);
		for(int i=1;i<K;i++) for (int j=i;j<K;j++) ans=min(ans,min({solve(s[j].x-s[i].x-1),solve(s[i].x-1+n-s[j].x),solve(s[j].x-1+n-s[i].x)}));
		printf("%lld",ans);
		return 0;
	}
}
char END;
int main(){
#ifdef HQ
	printf("Memory : %lld MB\n",(&BEGIN-&END)>>20);
//	freopen("03-02.in","r",stdin);
//	freopen(".out","w",stdout);
#endif
	hwq::main();
	return 0;
}
/*
2 4
2
1 1
1 4

4 4
3
1 4
2 2
3 3
专栏总结：https://www.luogu.com.cn/article/6030jn9i
实现框架：
	1. K^2枚举最外层的a+b
	2. 扫描线预处理加滑动窗口求解n行合法的c+d最小值 
实现细节： 
	1. 无脑开大数组，反正K都很小，别爆就行 
	2. 离散化t序列
	3. solve内不能直接统计答案，覆盖的行可能超过n，还需滑动窗口 
我天，1.25h想出来了，有进步，被提c+d那一步卡了一会，总的说还行
滑动窗口：最终可能是一个x区间内的东西提供贡献，如果K^2表示的话，要满足x[j]-(x[i]-len)+1>=n 
第一次觉得滑动窗口困难
f[i][j]要维护三个部分！！！0表示最前面，1表示中间，2表示最后面 
*/

评论

共 3 条评论，欢迎与作者交流。

正在加载评论...