P3375 KMP 题解

使用背景

暴力求解

KMP 算法

• next 数组

  此时可以建立一个 next 数组（或 nxt），作为一个转移数组。它的含义就是一个固定字符串的最长前缀与最长后缀相同的长度。
  如：
  abcdefgabc
  不难发现，在这个样例下，相同的最长前缀与最长后缀就是 abc。
  此时要注意，最长前缀是从第一个字符开始，但不包含最后一个字符。
  例如：
  kkkk
  他的最长前缀是 kkk。
  讲完上面的定义后，便进入正题。
  以字符串
  ababaca
  为例。
  我们用 next 数组来计算字符串中相同的最长前缀与最长后缀。方便理解，next 数组下标从 $0$ 开始，分别计算 a，ab，aba，abab，ababa，ababac，ababaca。
  显然得出，其对应为
  0. 无。a 只有一个字符，非相同，这是一个很重要的点。
  1. 无。ab 中 a 与 b 无法匹配。
  2. a，aba 中。
  3. ab，abab 中开头结尾两个 ab 匹配。
  4. aba，ababa 中先取前三个字符 aba，再取后三个字符 aba 匹配。
  5. 无。ababac 显然无法匹配。
  6. a，ababaca 开头结尾的两个 a 匹配。
  这时，next 数组已经赋值为了 {0, 0, 1, 2, 3, 0, 1}。
  我们想要用代码实现，可以用一张图来便于理解。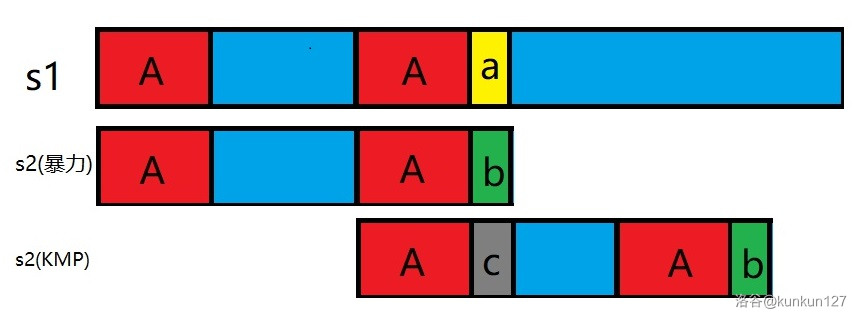
  
  上图中的 $A$ 是一样的。两个 $A$ 之间的也是一样的，我们发现 $a$ 和 $b$ 不一样。之前的算法是把下面的字符串往前移动一个距离，重新从头开始比较，那必然存在很多重复的比较。现在的做法是，我把下面的字符串往前移动，使 $s_1$ 尾部的 $A$ 和 $s_2$ 对齐，直接比较 $a$ 和 $c$ 是否一样。
  可以看到，匹配串每次往前移动，都是一大段一大段移动，假设匹配串里不存在重复的前缀和后缀，即 next 的值都是 $0$，那么每次移动其实就是一整个匹配串往前移动 $m$ 个距离。然后重新一一比较，这样就比较 $m$ 次，也就是，每次移动长度为 $m$ 的距离，比较 $m$ 次，移到末尾，就是比较 $n$ 次，时间复杂度为 $O(n)$。假设匹配串里存在重复的前缀和后缀，移动的距离相对小了，比较的次数也小了，但时间也是 $O(n)$。这就是 KMP 算法的好处。

代码实现

1. 求 next 数组（建议写成 nxt）
   CPP

   int len1 = s1.size(), len2 = s2.size();
   int j = 0;
   for (int i = 1; i < len2; i++)
   {
       while (j > 0 && s2[i] != s2[j]) j = nxt[j - 1];
       if (s2[i] == s2[j]) j++;
       nxt[i] = j;
   }
   

   外围的循环就是遍历整个 $s_2$，从 $1$ 开始寻找的原因就是刚刚所说的，单个字符无法构成最长前缀，直接从第二个字符开始查找。
   内层循环，如果 $j$ 此时大于 $0$，并且 $s2_i$ 与 $s2_j$ 不匹配，那么就进行回溯（$j = nxt_{j-1}$）。
   进入到下面的判断，此时如果 $s2_i$ 等于 $s2_j$，$j$ 加一。
   此时再将 $nxt_j$ 赋值为 $j$，也就是相同的最长前缀和最长后缀的长。
2. 进行 KMP。
   CPP

   for (int i = 0; i < len1; i++)
   {
      while (j > 0 && s1[i] != s2[j]) j = nxt[j - 1];
      if (s2[j] == s1[i]) j++;
      if (j == len2) cout << (i + 1) - len2 + 1 << endl, j = nxt[j - 1]; 
   }
   

   其实跟求 nxt 数组的过程差不多。只是我们不需要再更改 nxt 数组，而是当 $j$ 等于 $s_2$ 的长度时输出匹配成功的第一个字符的位置即可，再更新 $j$。

参考代码（模板）

#include <bits/stdc++.h>
using namespace std;
int nxt[1000005];
 
int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    int len1 = s1.size(), len2 = s2.size();
    int j = 0;
    for (int i = 1; i < len2; i++)
    {
        while (j > 0 && s2[i] != s2[j]) j = nxt[j - 1];
        if (s2[i] == s2[j]) j++;
        nxt[i] = j;
    }
    j = 0;
    bool flag = false;
    for (int i = 0; i < len1; i++)
    {
        while (j > 0 && s1[i] != s2[j]) j = nxt[j - 1];
        if (s2[j] == s1[i]) j++;
        if (j == len2) cout << (i + 1) - len2 + 1 << endl, j = nxt[j - 1], flag = true; 
    }
    for (int i = 0; i < len2; i++) cout << nxt[i] << ' ';
    return 0;
} 

时间复杂度