【Trick】prufer序列相关

定义：在一棵无根树中，每次删除最小的叶子并将叶子相连点编号加入序列。

性质：prufer序列与无根树一一对应

性质：大小为

n

的无根树的数量有

n^{n-2}

种，这同时也是完全图生成树的数量。

性质：每个结点在序列中出现的次数是其度数减一

建构：用一个指针维护目前最小的叶子，可以发现如果新出现的叶子比指针维护的叶子小，那么其可能出现的新的最小叶子为一根链，边跳边进序列即可，每个点最多被遍历两遍，复杂度

O(n)

。

CPP

void solve1() {
	for (int i = 1; i <= n - 1; i++) cin >> fa[i], deg[fa[i]]++;
	for (int i = 1, p = 1; i <= n - 2; i++, p++) {
		while (deg[p]) p++; // 自增找到下一个叶子结点
		pf[i] = fa[p]; // 加入序列
		while (i <= n - 2 && --deg[pf[i]] == 0 && pf[i] < p) // 如果产生新叶子结点且编号更小
			pf[i + 1] = fa[pf[i]], i++;
	}
}

还原：过程类似，不多赘述。

prufer序列还有很有趣的用途（来自oi-wiki）：

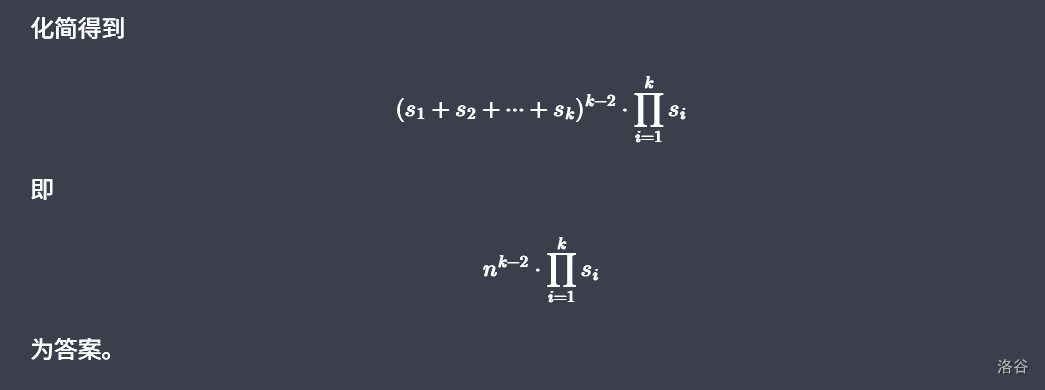
至于那个多元二项式定理，脑内展开一下

(x_1+...+x_m)^p

即可得到。

随机prufer序列的期望直径好像是

\sqrt{n}

的，我本来是为了这个性质来写文章的，但暂时找不到证明。

【Trick】prufer序列相关

文章操作

相关推荐

评论

【Trick】prufer序列相关