专栏文章

[ICPC 2025 Yokohama R] Seagull Population 题解

FFFTotoro
P14682题解参与者 2已保存评论 3

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
3 条
当前快照
1 份
快照标识符
@mkmfcq27
此快照首次捕获于
2026/01/20 18:01
4 周前
此快照最后确认于
2026/01/20 18:01
4 周前
查看原文
有一种直接的想法：记序列 bb（输入的序列）中的最小值为 mn\mathrm{mn}，构造 mn\mathrm{mn} 只海鸥使得它们全年都在海岛上，于是环就断成链了，问题转换为在一个新形成的序列 b′b'（满足 bi′=bi−mnb'_i=b_i-\mathrm{mn}）上求解。
将 b′b' 中任意一个为 00 的位置视为断开点（根据上面的定义一定存在这样的位置），不妨认为是 bn′b'_n（其他情况直接循环移位），问题变成了 [NOIP 2018 提高组] 铺设道路，新增加的答案为 f(b′)=∑i=1nmax⁡{bi′−bi−1′,0}f(b')=\sum\limits_{i=1}^n\max\{b'_i-b'_{i-1},0\}（认为 b0′=0b'_0=0），原因非常简单：若出现了比前一个元素大的元素，说明新增了若干只海鸥到岛上，新增的海鸥数量为两者的差值。构造方案可以借助一个栈，这样就可以得出若干仅有包含和相离关系的区间。称这个过程为新增加过程。
实现了这个做法后发现样例 33 无法通过。发现问题在于最开始的一步“构造 mn\mathrm{mn} 只全年在海岛上的海鸥”——由于海鸥可以跨年，所以可以在一个全年在岛上的海鸥中间“抠掉一段在岛上的时间”，然后将 b′b' 的一段区间 +1+1，从而让 f(b′)f(b') 更小。这么说可能有点抽象，下面将结合一张示例图具体地介绍这种方法。
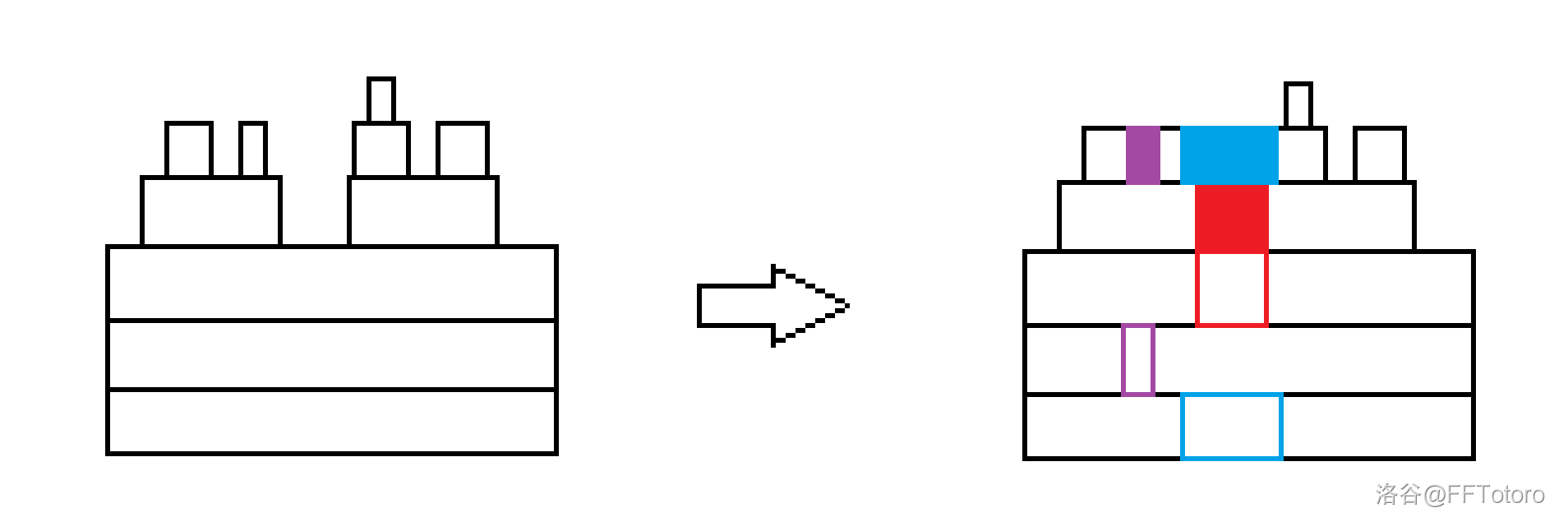
如图，底下那几层大的表示全年在岛上的海鸥，上面的几层表示必须新增的海鸥。根据上面描述的“新增加过程”，新增的区间只有包含与相离关系，意味着这是一个类似森林的结构。观察发现，操作的本质其实是合并两个区间，但不是所有区间都可以合并起来（因为有些是互相包含的）。紧接着可以发现，记这个森林的“高度”为 hh（例如，上图中描述的森林高度为 33），最终会留下最少 hh 个无法合并的区间（因为存在 hh 个区间是形如“一个包含一个”的链式结构）。而如果我们只合并“深度”相同的区间，则如果下面全年在海岛上的海鸥数量足够，就可以恰好留下 hh 个区间，因此这样的方法在所有合并区间的策略中是最优的。图片中展示了一种满足上述条件的合并方式。
接下来证明这种构造可以取到 mm 的下界。记 bb 中的最大值为 mx\mathrm{mx}，“新增加过程”产生的贡献为 f(b′)f(b')，则显而易见地有 m≥max⁡{mx,f(b′)}m\ge\max\{\mathrm{mx},f(b')\}。考虑上面的构造过程，当下面全年在岛上的海鸥足够合并所有能合并的区间时，对应的 m′m' 恰好等于 mx\mathrm{mx}（相当于每层都只有一个区间，下面加上面的总共有 mx\mathrm{mx} 层，于是就是 mx\mathrm{mx} 个区间）；否则，对应的 m′m' 恰好等于 f(b′)f(b')（下面一只全年在岛上的海鸥对应上面一个空位）。于是得出结论——这种构造是正确的。
时间复杂度 O(nlog⁡n)O(n\log n)，瓶颈在于一些排序。
放代码：
CPP
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=2e5;
int main(){
  ios::sync_with_stdio(false);
  cin.tie(0); cout.tie(0);
  int n; cin>>n;
  vector<int> a(n);
  for(auto &i:a)cin>>i;
  auto [mnp,mxp]=minmax_element(a.begin(),a.end());
  int mn=*mnp,mx=*mxp,p=mnp-a.begin();
  for(auto &i:a)i-=mn;
  rotate(a.begin(),mnp,a.end());
  // 把 0 转到最后一个位置
  ll m=0;
  stack<int> s;
  vector<tuple<int,int,int> > v;
  for(int i=1;i<=n;i++){
    if(i<n)m+=max(a[i]-a[i-1],0);
    if(m<=M){
      if(a[i%n]>a[i-1]){
        for(int j=0;j<a[i]-a[i-1];j++)
          s.emplace(i);
      } // 栈内压入新增区间左端点
      else{
        for(int j=0;j<a[i-1]-a[i%n];j++)
          v.emplace_back(a[i-1]-j,s.top(),i-1),s.pop();
      } // v 中记录的格式为：区间在森林中的“深度”，区间的左、右端点
    }
  }
  ll w=max(m,(ll)mx);
  if(cout<<w<<endl;w<=M){
    vector<pair<int,int> > vf;
    sort(v.begin(),v.end());
    while(v.size()>1&&mn){
      auto &[x1,l1,r1]=v.back();
      auto &[x2,l2,r2]=v[v.size()-2];
      if(x1!=x2)vf.emplace_back(l1,r1); // 不在同一层，不能合并
      else mn--,vf.emplace_back(l1,r2),r2=r1; // 在同一层，可以合并
      v.pop_back();
    } // 合并区间的过程
    for(auto [x,l,r]:v)
      vf.emplace_back(l,r);
    while(mn)vf.emplace_back(0,n-1),mn--;
    for(auto [l,r]:vf)
      cout<<(l+p)%n+1<<' '<<(r+p)%n+1<<'\n'; // 输出的时候记得把区间旋转回去
  }
  return 0;
}

评论

共 3 条评论，欢迎与作者交流。

正在加载评论...