这绝对是我写过的最神奇的考试题目。

——__H_J_M__

Part 1 赛事纪录（大事祭）

8:00 考场先开 T1，由于昨天写 T1 异常的顺利，因而我十分相信运气会顺延。

8:30 想了 30 分钟，什么都没想出来（除了暴力，部分分），但在这时，我抬头一看，Asa_fish 竟然已经开始对拍了，内心慌张。

8:40 写了一种特殊解，并借此发现了答案小于等于 3 的性质。

8:50 写了一种神奇的做法，并开始对拍。

9:00 开 T2。

9:30 T2 直接切掉了，并且开始写 T3。

10:10 听到了旁边的 GYC 一阵欢呼，原来是他 T2 也做出来了。

11:10 写完暴力后一直在想这道题 k=1 时的 DP 方程，费劲脑洞无法征服。

12:00 T4 写了一个贪心，写完后一侧大样利，才发现证伪了，还是写的特殊点。

12:30 又检查了一会 T1。

Part 2 题目

T1

T1 都十分简单，如果写不出来，一定是题目在诈骗你

——iChen

我当时的考场想法，不想看的跳过

首先，答案不大于三，为什么呢？

证明

CPP

aaa|a|a
aaa|a|a
aaa|a|a

像图中这样分割，就算是最坏情况（图中）我们也最多是 3

所以我当时的想法十分简单，既然这是一个万能方法，我直接特判不就是了吗？

可能是由于 Asa 的刺激，我虽然知道这是错的，仍然写了对拍

后来当然错了，于是我有想到了一个 "好办法"。

我直接大胆猜测不存在相同前缀长度超过 1 的情况，然后就这么 Ale

首先我先假设你已经知道了前文中的那个重要结论。

然后

一个直接的思路是枚举 $i, j$ 统计答案。考虑当前已经枚举了一个 $i$ ，如何找到最优的 $j$ 。对于 $b$ 的长度 < 3 的所有答案可以暴力枚举 $j$ ，只有 $O(1)$ 种。如果 $b$ 的长度 > 3，我们就不需要考虑 $j$ 的选取对 $a, b$ 字符串的影响，于是只考虑 $LCP(a, c)$ 和 $LCP(b, c)$ 的贡献。

可以让 $LCP(a, c) + LCP(b, c) = 0$ 当且仅当存在 $c_j \neq a_1 \land c_j \neq b_i$ 。否则：如果 $a_1 \neq b_i$ ，我们选 $j = n - 1$ 就有 $LCP(a, c) + LCP(b, c) = 1$ ，最优；如果 $a_1 = b_i$ ，那后面的 $c_j$ 也都和它们相等， $LCP(a, c) + LCP(b, c) \geq 2$ ，还是选 $j = n - 1$ 最优。

没啥好说得了，我的方法相当于在他的基础上多枚举了一些，当然完全没有证明

AC code

CPP

#include <bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e5+6;
int n;
int T;
int vis[27];
string a,b,c;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
struct node{
	int c[N];
	void add(int x,int k){
		for(int i=x;i<N;i+=(i&-i))
			c[i]+=k;
	}
	int ask(int x){
		int ans=0;
		for(int i=x;i>0;i-=(i&-i))
			ans+=c[i];
		return ans;
	}
}BIT[27];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
	cin>>T;
	while(T--){
		cin>>n;
		cin>>a>>b>>c;
		a=' '+a;
		b=' '+b;
		c=' '+c;
		for(int i=0;i<26;i++)
			memset(BIT[i].c,0,sizeof BIT[i].c);
		for(int i=1;i<=n;i++){
			BIT[b[i]-'a'].add(i,1);
		}
		int ANS=1e9;
		for(int p=n;p>=3;p--){
			for(int i=0;i<26;i++){
				if(BIT[i].ask(p-1)-BIT[i].ask(1)>0){
					ANS=min(ANS,(a[1]==(i+'a'))+(a[1]==c[p])+((i+'a')==c[p]));
				}
			}
		}
		cout<<ANS<<'\n';
	}
	return 0;
}

T2

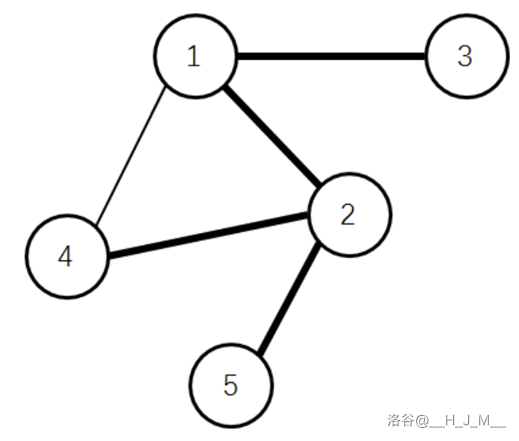
开局先看图

我们可以看一下样例中的 4 是如何出现的

这个图能够连接 (1-4),(1-5), 但为什么他们能连呢？

有两个条件：（x-y）

x 连接的是自己的祖宗节点
y 节点的儿子（路径上的）编号小于 x

所以直接用一个树状数组存储路径上的编号（除了 2）

AC code

code：

CPP

#include <bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=2e5+5,Mod=1e9+7;
int n;
int ans;
int tot,head[N],ver[N<<1],nxt[N<<1];
struct node{
	int c[N];
	void add(int x,int k){
		for(int i=x;i<N;i+=(i&-i))
			c[i]+=k;
	}
	int ask(int x){
		int ans=0;
		for(int i=x;i>0;i-=(i&-i))
			ans+=c[i];
		return ans;
	}
}BIT;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b){
	ver[++tot]=b;
	nxt[tot]=head[a],head[a]=tot;
}
void dfs(int x,int fa){
	ans+=BIT.ask(x-1);
	for(int i=head[x];i;i=nxt[i]){
		int y=ver[i];
		if(y==fa) continue;
		BIT.add(y,1);
		dfs(y,x);
		BIT.add(y,-1);
	}
}
int Pow(int x,int y){
	int ans=1;
	while(y){
		if(y&1) ans=ans*x%Mod;
		x=x*x%Mod,y>>=1;
	}
	return ans;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
	cin>>n;
	for(int i=1;i<n;i++){
		int a,b;cin>>a>>b;
		add(a,b),add(b,a);
	}
	dfs(1,0);
	cout<<Pow(2,ans)<<'\n';
	return 0;
}

T3

~~这不是人做的~~，Maybe

——__H_J_M__

暴力

\color{#52c41a} \mathcal {25tps}

TJ(仅供参考，防止PDF)

巡逻网络

k = 1

先考虑 k = 1，也即一维的情况。

整个题的贡献可以拆为三个部分：固定点内部互相的贡献、固定点与可选点之间的贡献、可选点内部互相的贡献。

第一种贡献是个定值，可以预处理出来；第二种贡献相当于在选择可选点的时候每个点会有一个额外权值，所以我们主要考虑第三部分，也即可选点内部之间的贡献如何处理。

考虑可选点，由于我们要求的是最大的曼哈顿距离和，且注意到绝对值本身就可以理解成最大值：

|a| + |b| = \max(a + b, a - b, -a + b, -a - b)

也就是说，绝对值比时无关紧要，我们只需要考虑安排好每个数每一维正负号的贡献就好了。

举个例子，假设已经选择了 m 个点，那么你可以先排序成

x_1 \leq x_2 \leq \cdots \leq x_m

，然后你按贡献计算

\sum_{i=1}^m (2i - m - 1)x_i = \sum_{j\neq i} |x_i - x_j|

。我们实际上只需要枚举 m! 种排列，然后将

\sum_{i=1}^m (2i - m - 1)x_i

的最大值算出来。

所以在一维的情况下，自然可以设一个 DP 出来：设

f(i, S)

表示前 i 个点中，已经设定了一些点位于 S 这些位置的情况下，所能产生的贡献最大值。此处的 S 应当是 m 位二进制数。也就是相当于用块压 DP 枚举了点坐标大小的 m! 种排列。

转移时，把第 i 个点放到第 p 个位置，贡献将会是

(2p - m - 1)x_i + c_i

，其中

c_i

表示第 i 个点与其他固定点之间的贡献。如此块压 DP，复杂度是

O(nm^2m)

，其中 n 代表可选点数，也即 m + t。

k = 2

其实本质上也没有什么区别，只是现在选择第 i 个点之后要同时考虑 x_i 和 y_i 的位置。

设

f(i, S_1, S_2)

表示前 i 个点中，已经设定了一些点的 x 坐标占据了 S_1 的位置，y 坐标占据了 S_2 的位置，所能产生的贡献最大值。

转移时，把第 i 个点的 x 坐标放到 p_1 的位置，y 坐标放到 p_2 的位置，贡献将会是

(2p_1 - m - 1)x_i + (2p_2 - m - 1)y_i + c_i

，复杂度粗略估计一下大概是

O(nm^2m)

，已经可以过了。

但是注意到，S_1 和 S_2 互相之间是有限制的，因为他们总需要保证出现的点数相同，不可能会是

O(4^m)

级别的状态量。实际上考虑枚举两个状态中出现的点数 k，状态量应当为

\sum_{k=0}^m \binom{m}{k}^2

这是

O(\frac{4^m}{\sqrt{m}})

的。

拓展

考虑一下有多次询问的情况，以及 k = 3.4 的情况怎么做？

T4

···

\color{white} \Huge \textsf {TA不应该出现在这里}

Part 3 展望未来

保T1T2，争T3T4。

赛前模拟2025/8/28

文章操作