专栏文章

各种三角形面积公式的证明、联系与优缺点

xxu_zhihao
算法·理论参与者 8已保存评论 7

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
7 条
当前快照
1 份
快照标识符
@mlmkmmb5
此快照首次捕获于
2026/02/15 01:09
5 天前
此快照最后确认于
2026/02/19 01:12
13 小时前
查看原文
作者：许智皓
摘要 三角形面积公式是连接几何图形与代数运算的重要桥梁。本文首先通过构造高线，利用勾股定理建立方程，几何代数结合地证明了秦九韶公式；进而，通过巧妙的代数恒等变形，将其转化为形式对称的海伦公式；最后，利用余弦定理与三角恒等式，揭示了秦九韶公式与正弦公式的统一性。论文不仅完成了三个公式的证明，更通过推导过程阐明了它们本质上源于同一几何关系（边与高）的不同代数表达，并对比了其在已知条件不同时的应用优势。

一、引言

三角形作为最基本的多边形，其面积计算是几何学的核心问题之一。从古埃及的土地丈量到现代计算机图形学，高效的面积求解方法始终具有重要价值。历史上，不同文化背景下的数学家沿着独特的思路。得出了形式各异却等价的三角形面积公式。
在西方，古希腊数学家海伦在其著作《度量》中记载了已知三边求面积的公式，即形式高度对称的海伦公式：
S=p(p−a)(p−b)(p−c)，其中 p=a+b+c2S = \sqrt{p(p-a)(p-b)(p-c)}，\quad 其中\ p=\frac{a+b+c}{2}
在东方，中国南宋数学家秦九韶在其巨著《数书九章》中独立提出了等价的 “三斜求积术”，其代数形式为：
S=144a2b2−(a2+b2−c2)2S = \frac{1}{4} \sqrt{4a^2b^2 - (a^2+b^2-c^2)^2}
随着三角学的发展，人们得到了更为直接的正弦公式，适用于已知两边及其夹角的情形：
S=12absin⁡C。S = \frac{1}{2} ab \sin C。
观察上述三个公式：海伦公式凸显对称之美，秦九韶公式展现直接运算，正弦公式则揭示边角关联。它们形式迥异，却服务于同一几何对象。这自然引发一系列思考：这些公式之间是否存在深刻的内在联系？它们是否源于同一个更为根本的几何原理？在实际应用中，面对不同的已知条件（如三边 SSSSSS、两边夹角 SASSAS），又应如何选择最优的计算路径以兼顾效率与精度？
因此，本文旨在从最基础的几何关系（底与高）出发，通过严谨的推导，系统地建立这三个公式之间的逻辑桥梁，阐明其本质上的统一性，并对比分析各自的优势与适用场景，从而揭示数学知识网络中有趣的连通性与和谐之美。

二、知识准备

  1. 余弦定理 c2=a2+b2−2abcos⁡Cc^2=a^2+b^2-2ab\cos{C}，以及其在直角三角形中的特殊情况——勾股定理 c2=a2+b2c^2=a^2+b^2。（由于 cos⁡90∘=0\cos {90^\circ}=0）。
  2. 三角形恒等式 sin⁡2θ+cos⁡2θ=1\sin^2 \theta+\cos^2 \theta=1。
  3. 三角形面积公式（面积为底与高的积的一半）。

三、主要证明过程

  • 秦九韶公式
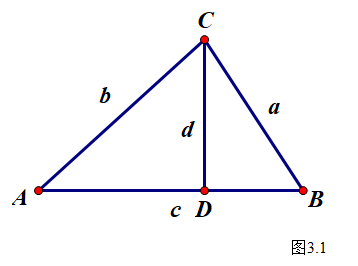
  1. 建立模型
建立一个如图 3.13.1 的模型，其中 CDCD 是 △ABC\bigtriangleup ABC 中 ABAB 边上的高。设 AB=c,BC=a,AC=b,BD=dAB=c,BC=a,AC=b,BD=d。
  1. 设元得出方程求解面积
设 x=ADx=AD，在 Rt△ACDRt\bigtriangleup{ACD} 和 Rt△BCDRt\bigtriangleup{BCD} 中，根据勾股定理分别可得：
CD2=AC2−AD2CD2=BC2−BD2 CD^2=AC^2-AD^2\\ CD^2=BC^2-BD^2
联立两式可得：
AC2−AD2=BC2−BD2 AC^2-AD^2=BC^2-BD^2
可得方程：
b2−x2=a2−(c−x)2 b^2-x^2=a^2-(c-x)^2
可解的 xx 的解为 x=b2+c2−a22cx=\frac{b^2+c^2-a^2}{2c}。故 d=b2−x2=b2−(b2+c2−a22c)2d=\sqrt{b^2-x^2}=\sqrt{b^2-(\frac{b^2+c^2-a^2}{2c})^2}，故 S△ABC=12cd=12cb2−(b2+c2−a22c)2=144b2c2−(b2+c2−a2)2S_{\bigtriangleup{ABC}}=\frac{1}{2} cd=\frac{1}{2} c\sqrt{b^2-(\frac{b^2+c^2-a^2}{2c})^2}=\frac{1}{4} \sqrt{4b^2c^2-(b^2+c^2-a^2)^2}。
  1. 从特殊到一般
S△ABC=144b2c2−(b2+c2−a2)2S_{\bigtriangleup{ABC}}=\frac{1}{4} \sqrt{4b^2c^2-(b^2+c^2-a^2)^2} 其实就是秦九韶公式的应用。对于高在外部的三角形也可以得出类似结论，这里不多赘述。
不难发现，对于一般的三角形，若三边长分别为 a,b,ca,b,c，其面积可以表示为 S=144a2c2−(a2+c2−b2)2=144a2c2−(a2+c2−b2)2=144b2c2−(b2+c2−a2)2S=\frac{1}{4} \sqrt{4a^2c^2-(a^2+c^2-b^2)^2}=\frac{1}{4} \sqrt{4a^2c^2-(a^2+c^2-b^2)^2}=\frac{1}{4} \sqrt{4b^2c^2-(b^2+c^2-a^2)^2}（轮换式对称），即秦九韶公式得证。
  • 海伦公式
海伦公式其实就是秦九韶公式的变形，下面是根据已经证明的秦九韶公式来推导海伦公式：
推导的过程看似繁琐，但目标明确：将秦九韶公式根号内的表达式，因式分解为关于边长和半周长（pp）的对称形式。关键技巧是反复使用平方差公式。
S=144a2c2−(a2+c2−b2)2 =a2c24−(a2+c2−b2)242                               =(ac2+a2+c2−b24)(ac2−a2+c2−b24)                                 =(2ac+a2+c2−b24)(2ac−a2−c2+b24)               =((a+c)2−b24)(b2−(a−c)24)                                             =((a+c+b)(a+c−b)4)((b−a+c)(b+a−c)4)                                         =(a+c+b2)(a+c−b2)(b−a+c2)(b+a−c2)                                                    =(a+b+c2)(a+b+c2−b)(a+b+c2−a)(a+b+c2−c)S =\frac{1}{4} \sqrt{4a^2c^2-(a^2+c^2-b^2)^2} \\ \ =\sqrt{\frac{a^2c^2}{4}-\frac{(a^2+c^2-b^2)^2}{4^2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{(\frac{ac}{2}+\frac{a^2+c^2-b^2}{4})(\frac{ac}{2}-\frac{a^2+c^2-b^2}{4})}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{(\frac{2ac+a^2+c^2-b^2}{4})(\frac{2ac-a^2-c^2+b^2}{4})} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \sqrt{(\frac{(a+c)^2-b^2}{4})(\frac{b^2-(a-c)^2}{4})}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{(\frac{(a+c+b)(a+c-b)}{4})(\frac{(b-a+c)(b+a-c)}{4})}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{(\frac{a+c+b}{2})(\frac{a+c-b}{2})(\frac{b-a+c}{2})(\frac{b+a-c}{2})}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{(\frac{a+b+c}{2})(\frac{a+b+c}{2}-b)(\frac{a+b+c}{2}-a)(\frac{a+b+c}{2}-c)}
然后设 p=a+b+c2p=\frac{a+b+c}{2}，所以 S=p(p−a)(p−b)(p−c)S=\sqrt{p(p-a)(p-b)(p-c)}，即海伦公式得证。
  • 三角形面积的正弦公式
正弦公式的证明可以独立进行，但为了体现公式间的联系，我们展示如何从秦九韶公式自然地推导出它。
由余弦定理变形可得 cos⁡C=a2+b2−c22ab\cos C=\frac{a^2+b^2-c^2}{2ab}，由三角形恒等式 sin⁡2θ+cos⁡2θ=1\sin^2 \theta+\cos^2 \theta=1 变形得 sin⁡2C=1−cos⁡2C=1−(a2+b2−c22ab)2\sin^2 C=1-\cos^2C=1-(\frac{a^2+b^2-c^2}{2ab})^2。以下是根据秦九韶公式来推导三角形面积的正弦公式的过程：
S=144a2b2−(a2+b2−c2)2         =144a2b2[1−(a2+b2−c22ab)2]=144a2b2sin⁡2C=12absin⁡CS=\frac{1}{4} \sqrt{4a^2b^2-(a^2+b^2-c^2)^2} \\ \ \ \ \ \ \ \ \ \ =\frac{1}{4} \sqrt{4a^2b^2[1-(\frac{a^2+b^2-c^2}{2ab})^2]}\\ =\frac{1}{4} \sqrt{4a^2b^2\sin^2 C}\\ =\frac{1}{2} ab \sin C

四、应用举例与数值比较

为了直观展示三个公式的应用，并对比其计算过程的特点，我们考虑一个具体的三角形实例：
例题：已知三角形三边长分别为 a=13a=13，b=14b=14，c=15c=15。求其面积 SS。

1. 使用秦九韶公式计算

公式：S=144a2b2−(a2+b2−c2)2S = \frac{1}{4} \sqrt{4a^2b^2 - (a^2 + b^2 - c^2)^2}
计算步骤：
  1. 计算各项：
    a2=169,b2=196c2=225a^2 = 169, \quad b^2 = 196 \quad c^2 = 225
    a2+b2−c2=169+196−225=140a^2 + b^2 - c^2 = 169 + 196 - 225 = 140
    4a2b2=4×169×196=4×33124=1324964a^2b^2 = 4 \times 169 \times 196 = 4 \times 33124 = 132496
    (a2+b2−c2)2=1402=19600(a^2 + b^2 - c^2)^2 = 140^2 = 19600
  2. 代入公式：
    S=14132496−19600=14112896S = \frac{1}{4} \sqrt{132496 - 19600} = \frac{1}{4} \sqrt{112896}
  3. 开方与化简：
    112896=336(因为3362=112896)\sqrt{112896} = 336 \quad (\text{因为} 336^2 = 112896)
    S=14×336=84S = \frac{1}{4} \times 336 = 84
结果：S=84S = 84
特点：计算过程为单一的代数运算流程，逻辑直接，但涉及较大数字的乘方与减法。

2. 使用海伦公式计算

公式：S=p(p−a)(p−b)(p−c),其中 p=a+b+c2S = \sqrt{p(p-a)(p-b)(p-c)},\quad 其中\ p=\frac{a+b+c}{2}
计算步骤：
  1. 计算半周长 pp：
    p=13+14+152=422=21p = \frac{13 + 14 + 15}{2} = \frac{42}{2} = 21
  2. 计算各差值：
    p−a=21−13=8p - a = 21 - 13 = 8
    p−b=21−14=7p - b = 21 - 14 = 7
    p−c=21−15=6p - c = 21 - 15 = 6
  3. 计算乘积并开方： p(p−a)(p−b)(p−c)=21×8×7×6p(p-a)(p-b)(p-c) = 21 \times 8 \times 7 \times 6
    计算顺序可灵活调整以简化：
    21×6=126,8×7=56 21 \times 6 = 126,\quad 8 \times 7 = 56
    126×56=7056126 \times 56 = 7056
    S=7056=84S = \sqrt{7056} = 84
结果：S=84S = 84
特点：计算步骤规整、对称，数字通常较小（尤其是半周长及其差值），心算或手算不易出错，体现了公式的优美与实用性。

3. 使用正弦公式计算

公式：S=12absin⁡CS = \frac{1}{2} ab \sin C
计算步骤： 前提：已知三边，需先利用余弦定理求出角 CC。
  1. 由余弦定理求 cos⁡C\cos C：
    cos⁡C=a2+b2−c22ab=169+196−2252×13×14=140364=513\cos C = \frac{a^2 + b^2 - c^2}{2ab} = \frac{169 + 196 - 225}{2 \times 13 \times 14} = \frac{140}{364} = \frac{5}{13}
  2. 由 sin⁡2C+cos⁡2C=1\sin^2 C + \cos^2 C = 1 求 sin⁡C\sin C：
    sin⁡2C=1−(513)2=1−25169=144169\sin^2 C = 1 - (\frac{5}{13})^2 = 1 - \frac{25}{169} = \frac{144}{169}
    sin⁡C=144169=1213(∠C为锐角,取正值)\sin C = \sqrt{\frac{144}{169}} = \frac{12}{13} \quad(\angle C \text{为锐角,取正值})
  3. 代入正弦公式：
    S=12×13×14×1213=12×14×12=7×12=84S = \frac{1}{2} \times 13 \times 14 \times \frac{12}{13} = \frac{1}{2} \times 14 \times 12 = 7 \times 12 = 84
结果：S=84S = 84
特点：当已知两边及其夹角（SASSAS）时，此公式是最直接、最快捷的选择。但在本例仅知三边（SSSSSS）的条件下，需要先解角，增加了计算步骤，反而显得繁琐。

4. 综合比较与结论

公式适用条件计算步骤数计算复杂度本例特点优势场景
秦九韶公式SSSSSS中等较高直接代数运算，数字较大编程实现时逻辑直接，无需先求半周长
海伦公式SSSSSS少且规整低数字小，乘法与开方简单，最便于手算已知三边时手算的首选，易于记忆和检查
正弦公式SASSAS多高需先求角，引入了三角函数已知两边夹角时的唯一直接公式，非常便捷
对于非常“扁平”的三角形（例如两边之和几乎等于第三边），海伦公式中的 p−cp-c 会非常接近 00，在计算机浮点运算中可能导致精度损失。此时，秦九韶公式或重新安排计算顺序的算法可能数值稳定性更优。但在绝大多数常规计算中，三个公式结果一致。
结论：通过同一道例题的验算，我们验证了三个公式的等价性。在选择公式时，应优先考虑已知条件：
  • 若已知三边（SSSSSS），首选海伦公式。
  • 若已知两边及其夹角（SASSAS），首选正弦公式。
  • 秦九韶公式作为代数形式的核心，在理论推导和特定计算中具有独特价值。
这种“一题多解”的对比，生动体现了数学的灵活性——通往正确答案的道路不止一条，而最合适的路径往往取决于我们手中的已知条件。

五、结论与感想

通过上述的过程，我们成功地证明了三种求三角形面积公式的正确性，通过推导的过程中，我们发现了三种公式的优点：
  • 秦九韶公式：它同样是已知三边（SSSSSS）时的选择。虽然在形式上不如海伦公式优美，但在某些手算或编程计算场景下，因其根号内为单一多项式，可能更利于数值稳定性或代数变形。
  • 海伦公式：当已知三边边长（SSSSSS）时，这是最对称、最便于记忆的公式。尽管计算涉及四次乘法，但流程规整，不易出错。
  • 三角形面积的正弦公式：公式直接关联边角，适合在已知一角两边的三角形（SASSAS）中，是求面积最直接、最快捷的解决方式。
感悟：数学中，通往同一结论的道路往往不止一条。从一条简单的几何高线出发，通过不同的代数视角，竟能演绎出三个各具特色的面积公式。这不仅锻炼了我们的逻辑推理能力，更让我们体会到数学内在的和谐与统一之美。探索公式之间的联系，远比记忆公式本身更有趣味，也更为重要。
这正应了那句古语：“道法三千六百门，而人人各执一苗根。”数学之道亦如是，通往真理的路径众多，关键在于理解其内在的贯通与联系，而非固守一隅。
参考文献
  • 秦九韶《数书九章》
  • Heath，T. L. A History of Greek Mathematics（海伦公式历史）
日期：20262026 年 22 月
AI 使用说明
本文在写作完成后使用 DeepSeek 进行了润色。保本文的论证过程和重要结论都是自主完成的。

评论

共 7 条评论，欢迎与作者交流。

正在加载评论...