前言

作者 @__CrossBow_EXE__ 在 2025.5.19 学完了 FFT 后，感觉脑子不够用，因此作此文章。

FFT 太强了！

前置芝士

复数
多项式
函数

不了解也没关系，马上就会介绍。

复数

众所周知，

\sqrt {-1}=i

。

i

称作虚数单位。形似

a+bi

的数叫做复数。复数的基本运算如下：

$(a+bi)+(a'+b'i)=(a+a')+(b+b')i$
$(a+bi)\times(a'+b'i)=aa'-bb'+(a'b+ab')i$

如果我们把实数轴看作横坐标，虚数轴看作纵坐标，我们就有了一个坐标系，称为复平面。每个实数或虚数都能在复平面上表示。如图：

而上图中的

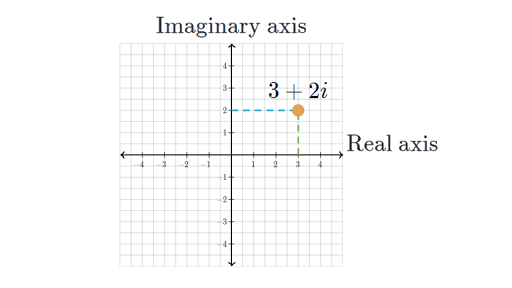
3+2i

可以看作一个从

(0,0)

指向

(3,2)

的向量。向量听起来高大上，其实就是一个有向线段。

接着，我们作一个圆，圆心为

(0,0)

，半径为

1

。根据圆的定义，每个从原点指向圆上一点的向量长度都为

1

。假设一个向量与实数轴的夹角为

\theta

，如下图：

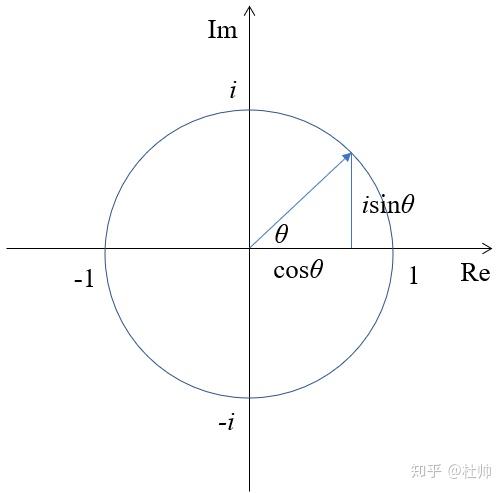
根据三角函数，我们知道：这个直角三角形三条边的长度分别为

\cos \theta

，

\sin \theta

，

1

。恰好这是一个直角三角形，满足勾股定理，于是就有我们的第一个公式：

\cos^2 \theta + \sin^2 \theta=1

我们还需要知道单位根。如果我们把单位圆给

n

等分，那我们就有了

n

个向量。为了表示每个向量，我们引入符号

\omega_n^i

，其中

n

为等分的数量，后面整篇文章默认

n

为

2

的幂，

i

不是虚数。（得后遗症了？）

我们把指向正右方的向量记作

\omega^0_n

，接着逆时针标上

\omega^1_n,\omega^2_n,\dots,\omega^{n-1}_n

。如下图：

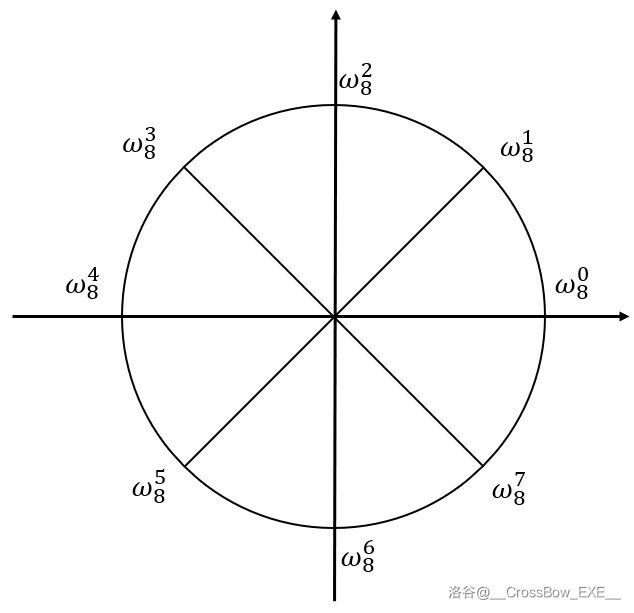
单位根有许多好玩~~但并不简单~~的性质：

还记得上面的公式吗？每一个单位根都可以通过这个公式的变形得到： $\omega_n^k=\cos k\times\frac{2\pi}{n}+i\sin k \times \frac{2\pi}{n}$ 。
单位根可以“约分”： $\omega^{ka}_{kb}=\omega^a_b$ 。很容易理解，比如六等分的第三个就相当于二等分的第一个。
$\omega^{k+n/2}_n=-\omega^k_n$ 。也很容易理解，右边相当于左边转了半圈。

多项式的表示法

假设我们有一个多项式

f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n

，显然我们可以用

a

数组

\{a_0,a_1,a_2,\dots,a_n\}

来表示它。这叫做一个多项式的系数表示法。

但计算机在处理它时效率很低。考虑把多项式看作一个函数。众所周知，两点确定两个项的一次函数，三点确定三个项的二次函数，那么多项式作为一个

n+1

个项的

n

次函数，肯定可以用

n+1

个点表示。即：选取

n+1

个横坐标，按照函数算出纵坐标，把所有点的坐标都列出来。这是多项式的点值表示法。

有一件很显然的事：系数表示法和点值表示法是可以互推的。FFT 就是在干这件事。

FFT 思想

如果我们要计算两个多项式的乘积，复杂度是

O(size^2)

的。快速傅里叶变换可以运用上面两个知识，把这个过程变为

O(n \log n)

的。

我们假设有一个多项式

f(x)

。它的系数表示法显然是

f(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}

。对它做如下变化：

f(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}

把下标按奇偶分类，

f(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+\dots+a_{n-1}x^{n-1})

把后面的括号提出

x

，

f(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+\dots+a_{n-1}x^{n-2})

稍作整理，

f(x)=f'(x^2)+xf''(x^2)

但是，如果我们随便带入一个

x

，复杂度依旧是

O(n^2)

的。那我们应该带入什么呢？

没错，代入复数！~~想一想，为什么。~~

将

\omega^k_n

带入后，还不能轻举妄动，需要分类讨论。

$k \le \frac{n}{2}$

\begin{aligned} f(\omega^k_n) &= f'(\omega^{2k}_n) + \omega^k_nf''(\omega^{2k}_n) \\ &= f'(\omega^k_{n/2})+\omega^k_nf''(\omega^k_{n/2}) \end{aligned}

$k > \frac{n}{2}$ ，那么 $k$ 就相当于 $k'+\frac{n}{2}$

\begin{aligned} f(\omega^k_n) &= f'(\omega^{2k+n}_n) + \omega^{k+\frac{n}{2}}_nf''(\omega^{2k+n}_n) \\ &= f'(\omega^k_{n/2})-\omega^k_nf''(\omega^k_{n/2}) \end{aligned}

看着复杂，其实对着图很快就能推出来。

不难发现，两个式子只有中间的符号上有区别。

而我们只需要把所有

\omega^k_{n/2}

带入

f'

和

f''

，就能求出来

f

的值了。那么怎么带入

f'

和

f''

呢？仿照上面的过程，递归实现即可。

这样问题每次都能减少一半（

n

变成了

n/2

），共有

\log n

层，而我们需要带入

n

个数，复杂度来到了

O(n \log n)

！

上面的过程是把系数表示法转为点值表示法，称作 DFT。怎么再转回来呢？这需要用到单位根反演的知识，~~老师上课也没讲~~，这里剧透一下：把欧拉公式中的加号改成减号即可。这个转回来的过程乘坐 IDFT。它与 DFT 的差别仅在正负号上。

因此，在代码实现时，不必分两个函数；而是在一个函数中加上一个参数

type

，往里传

1

或

-1

，函数中就用

type

乘上

\sin

后面那一坨即可。

知道了这些，我们就能写出最基础的 FFT 代码了。

递归版 FFT 代码

CPP

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
int n,m;
const double PI=acos(-1);
const int N=2000005;
struct num{
	double x,y;//x+yi
	num(double xx=0,double yy=0){x=xx,y=yy;}
	num operator +(num const &B) const{return num(x+B.x,y+B.y);}
	num operator -(num const &B) const{return num(x-B.x,y-B.y);}
	num operator *(num const &B) const{return num(x*B.x-y*B.y,x*B.y+y*B.x);}
	//除法没用
}f[N<<1],g[N<<1],tmp[N<<1];
void fft(num *f,int len,int type){
	if(len==1) return;//边界条件
	num *f0=f,*f1=f+(len>>1);
	for(int i=0;i<len;i++) tmp[i]=f[i];//缓存
	for(int i=0;i<(len>>1);i++){//分奇偶打乱
		f0[i]=tmp[i<<1];
		f1[i]=tmp[i<<1|1];
	}
	//分治
	fft(f0,len>>1,type);
	fft(f1,len>>1,type);
	num t(cos(2*PI/len),type*sin(2*PI/len)),buf(1,0);
	for(int i=0;i<(len>>1);i++){
		tmp[i]=f0[i]+buf*f1[i];
		tmp[i+(len>>1)]=f0[i]-buf*f1[i];
		buf=buf*t;//旋转
	}
	for(int i=0;i<len;i++) f[i]=tmp[i];//放回
}
int ans[N];
signed main(int argc,char *argv[]){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ios::sync_with_stdio(NULL);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=0;i<=n;i++) cin>>f[i].x;
	for(int i=0;i<=m;i++) cin>>g[i].x;
	int lim=1;
	for(;lim<=n+m;lim<<=1);
	fft(f,lim,1);fft(g,lim,1);
	for(int i=0;i<=lim;i++){
		f[i]=f[i]*g[i];
	}
	fft(f,lim,-1);
	for(int i=0;i<=lim;i++) ans[i]+=int(f[i].x/lim+0.5);
	for(int i=0;i<=n+m;i++) cout<<ans[i]<<' ';
	cout<<endl;
	return 0;
}
/*
---INFORMATIONS---
TIME:2025-05-19 08:53:45
PROBLEM:P3803
CODE BY __CrossBow_EXE__ Luogu uid967841
*/

注意到代码中的结构体了吗？那是我手工实现的复数类。虽说 STL 自带一个复数类 complex，但毕竟手工的更安心。

但是众所周知，递归的常数很大。为了解决这个问题，又有了非递归版的 FFT。

蝴蝶变换与非递归版 FFT

在讲非递归的 FFT 前，先来说一下如何优化。优化的方法叫做蝴蝶变换。

先来看这张图，很清晰地展示了 FFT 的递归过程：

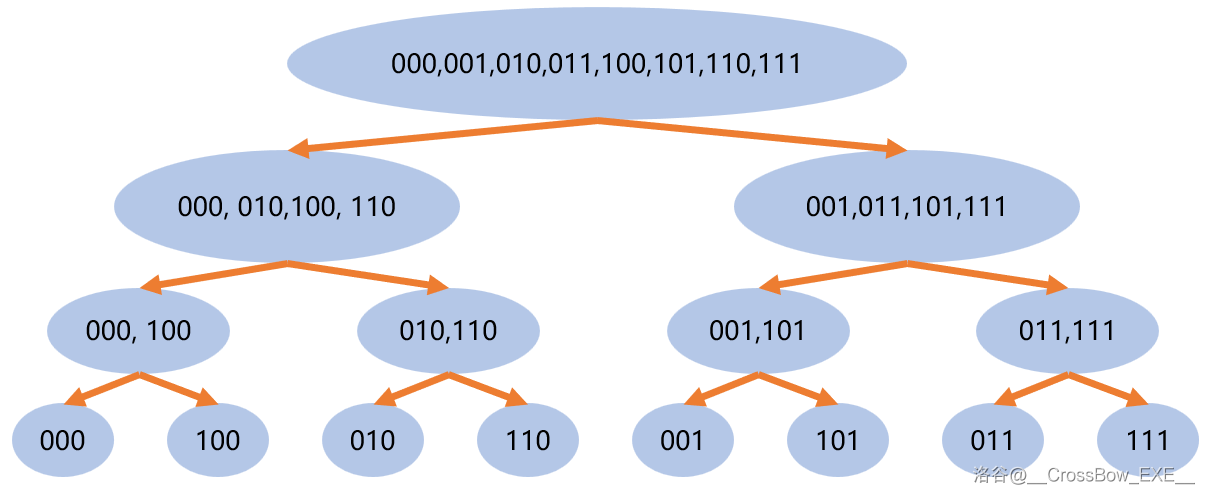
没看懂？再看这张图，注意叶子节点的二进制和它到根的路径的关系：

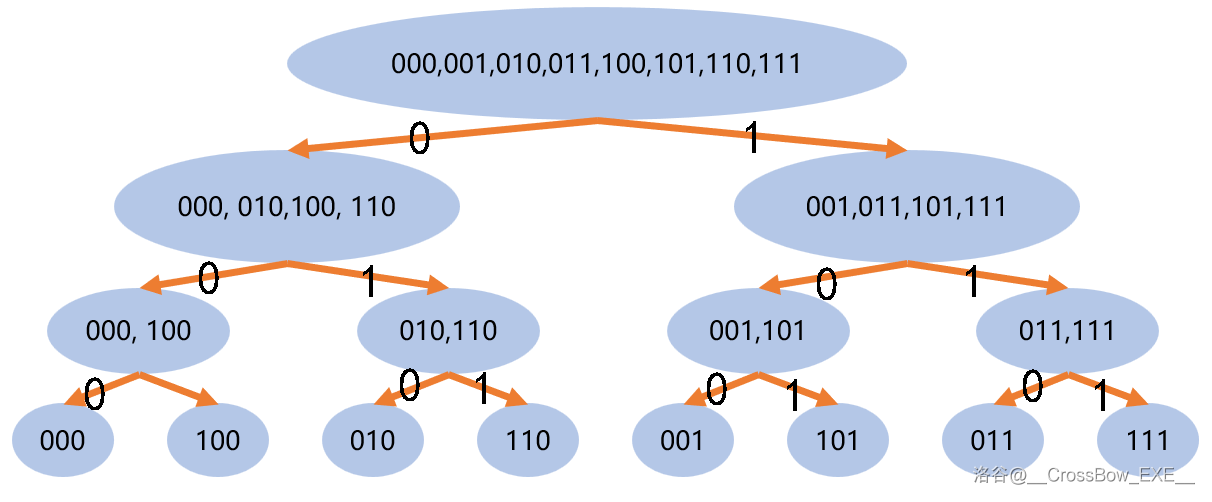
可以发现，每个叶子节点到根的路径都可以表示为一个 01 串，而这个 01 串刚好和这个叶子节点的二进制相同。反过来讲，从根节点到每个叶子节点的路径，刚好是叶子节点的二进制反过来。

还记得我们的代码吗？注意到在递归分治之前，只是把位置给调换过来了。如果我们提前就把位置摆好，是不是就不用递归了呢？知道了顺序，直接从叶子节点网上算不就搞定了？

换句话说，运算顺序可以表示为这张图：

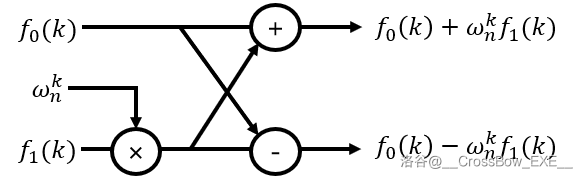
正因为这张图长得像一只蝴蝶，因此取名为“蝴蝶变换”。（哪里像了？）

CPP

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
int n,m;
const double PI=acos(-1);
const int N=2000005;
int r[N<<1];
struct num{
	double x,y;//x+yi
	num(double xx=0,double yy=0){x=xx,y=yy;}
	num operator +(num const &B) const{return num(x+B.x,y+B.y);}
	num operator -(num const &B) const{return num(x-B.x,y-B.y);}
	num operator *(num const &B) const{return num(x*B.x-y*B.y,x*B.y+y*B.x);}
	//除法没用
}f[N<<1],g[N<<1],tmp[N<<1];
void fft(num *f,int lim,int type){
	for(int i=0;i<lim;i++){//重新排列元素
		if(i<r[i]) swap(f[i],f[r[i]]);
	}
	for(int mid=1;mid<lim;mid<<=1){//当前区间长度
		num t(cos(PI/mid),type*sin(PI/mid));//单位根初始化
		for(int len=mid<<1,j=0;j<lim;j+=len){
			num w(1,0);//平躺单位根
			for(int i=0;i<mid;i++,w=w*t){//旋转
				num x=f[i+j],y=w*f[i+j+mid];
				f[i+j]=x+y;
				f[i+j+mid]=x-y;
			}
		}
	}
}
int ans[N];
int L;
signed main(int argc,char *argv[]){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ios::sync_with_stdio(NULL);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=0;i<=n;i++) cin>>f[i].x;
	for(int i=0;i<=m;i++) cin>>g[i].x;
	int lim=1;
	for(;lim<=n+m;lim<<=1,L++);
	for(int i=0;i<=lim;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
	fft(f,lim,1);fft(g,lim,1);
	for(int i=0;i<=lim;i++){
		f[i]=f[i]*g[i];
	}
	fft(f,lim,-1);
	for(int i=0;i<=lim;i++) ans[i]+=int(f[i].x/lim+0.5);
	for(int i=0;i<=n+m;i++) cout<<ans[i]<<' ';
	cout<<endl;
	return 0;
}

注意到主函数中新加的对

r

数组的预处理了吗？一大坨位运算，或许是新手最不容易理解的部分了。这里引用老师课件上的解释（有改动）：

一个简单的递推过程，观察一下：

r[i>>1] 相当于把最后一位砍掉，也就是把路径的最高位砍掉了。这样最高位就会凭空冒出一个 $0$ 。为了把这个 $0$ 也砍掉，再右移一位，就变成了 r[i>>1]>>1。

这样一来，我们就把除了最高位的所有位都倒了过来。那我们再把最高位补上，也就有了后面 |((i&1)<<(L-1)) 的部分。

你看懂了吗？反正我没看懂，背过就完了。

但还能优化！上面的代码调用了三次 FFT，可以把它优化到只调用两次！

终极优化版 FFT

注意到，如果一个复数平方，式子如下：

(a+bi)^2=a^2-b^2+2abi

后面的

2abi

不正是我们想要的、和

i

相乘的部分吗？因此我们可以只开一个表示函数的数组，它的实数部分存一个函数，虚数部分存另一个函数，自己乘自己平方即可。

但这样精度损失比较严重，有时用不了。

CPP

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
int n,m;
const double PI=acos(-1);
const int N=2000005;
int r[N<<1];
struct num{
	double x,y;//x+yi
	num(double xx=0,double yy=0){x=xx,y=yy;}
	num operator +(num const &B) const{return num(x+B.x,y+B.y);}
	num operator -(num const &B) const{return num(x-B.x,y-B.y);}
	num operator *(num const &B) const{return num(x*B.x-y*B.y,x*B.y+y*B.x);}
	//除法没用
}a[N<<1];
void fft(num *f,int lim,int type){
	for(int i=0;i<lim;i++){//重新排列元素
		if(i<r[i]) swap(f[i],f[r[i]]);
	}
	for(int mid=1;mid<lim;mid<<=1){//当前区间长度
		num t(cos(PI/mid),type*sin(PI/mid));//单位根初始化
		for(int len=mid<<1,j=0;j<lim;j+=len){
			num w(1,0);//平躺单位根
			for(int i=0;i<mid;i++,w=w*t){//旋转
				num x=f[i+j],y=w*f[i+j+mid];
				f[i+j]=x+y;
				f[i+j+mid]=x-y;
			}
		}
	}
	if(type==-1){
		for(int i=0;i<lim;i++){
			a[i].x/=lim;
			a[i].y/=lim;
		}
	}
}
int ans[N];
int L;
signed main(int argc,char *argv[]){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ios::sync_with_stdio(NULL);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=0;i<=n;i++) cin>>a[i].x;
	for(int i=0;i<=m;i++) cin>>a[i].y;
	int lim=1;
	for(;lim<=n+m;lim<<=1,L++);
	for(int i=0;i<=lim;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
	fft(a,lim,1);
	for(int i=0;i<=lim;i++) a[i]=a[i]*a[i];
	fft(a,lim,-1);
	for(int i=0;i<=n+m;i++){
		cout<<int(a[i].y/2+0.5)<<' ';
	}
	return 0;
}

这种优化叫做三步变两步优化。~~不过我管它叫虚实相乘。~~

例题

我们这种蒟蒻做不了太难的题，只能来个模板题练手。值得注意的是，上面三种代码都能通过。它们的对比如下：

	时间	空间
递归版 FFT	$3.19s$	$191.59MB$
非递归版 FFT	$2.40s$	$200.82MB$
三步变两步 FFT	$1.61s$	$72.59MB$

现在知道该背谁了吧？

但还没完！在测试中发现，STL 自带的 complex 居然比手写复数类快！

	时间	空间
三步变两步 FFT+STL 自带复数类	$1.45s$	$43.52MB$

因此，请大喊三声：

STL 太强了！

什么？你不会用？可以去看附录。

习题

这里直接给出老师讲的例题。

还有高精乘，就不放链接了。

参考资料

拓展阅读

快速数论变换
快速沃尔什变换
Dirichlet 卷积
多项式全家桶（慎入！可能做一道就回不来了！）

附录

STL 自带的复数类 complex 貌似比手写的快？这下不得不介绍了。

首先，使用它需要导入头文件 complex。

创建一个复数很简单，只需要

CPP

complex<T> num;

即可。其中 T 为数据类型。

众所周知，复数分为实部和虚部。而 num.real() 可以访问 num 的实部，num.imag() 可以访问它的虚部。

复数之间的四则运算 STL 都帮你重载了，直接用即可。

复数显然不能比较大小。

下面给出使用 complex 后的模板题代码：

CPP

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
#define num complex<double>
using namespace std;
int n,m;
const double PI=acos(-1);
const int N=2000005;
int r[N<<1];
num a[N<<1],t,w,x,y;
double tmp;
void fft(num *f,int lim,int type){
	for(int i=0;i<lim;i++){//重新排列元素
		if(i<r[i]) swap(f[i],f[r[i]]);
	}
	for(int mid=1;mid<lim;mid<<=1){//当前区间长度
		t=num(cos(PI/mid),type*sin(PI/mid));//单位根初始化
		for(int len=mid<<1,j=0;j<lim;j+=len){
			w=num(1,0);//平躺单位根
			for(int i=0;i<mid;i++,w=w*t){//旋转
				x=f[i+j],y=w*f[i+j+mid];
				f[i+j]=x+y;
				f[i+j+mid]=x-y;
			}
		}
	}
	if(type==-1){
		for(int i=0;i<lim;i++){
			a[i]/=lim;
		}
	}
}
int ans[N];
int L;
signed main(int argc,char *argv[]){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ios::sync_with_stdio(NULL);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=0;i<=n;i++) cin>>a[i];
	for(int i=0;i<=m;i++) cin>>tmp,a[i].imag(tmp);
	int lim=1;
	for(;lim<=n+m;lim<<=1,L++);
	for(int i=0;i<=lim;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
	fft(a,lim,1);
	for(int i=0;i<=lim;i++) a[i]=a[i]*a[i];
	fft(a,lim,-1);
	for(int i=0;i<=n+m;i++){
		cout<<int(a[i].imag()/2+0.5)<<' ';
	}
	return 0;
}

后记

本文或许是作者写的第一篇学习笔记。会有后人看到吗？

希望这一篇文章能让你走进多项式运算的神奇世界，感受爆切紫题的快乐。

依然有一些无聊的统计：本文共

11544

字，

6

张图片，

12

个超链接，手搓了

10

个公式，花费了

2

天时间。

本文将会发表在作者 @__CrossBow_EXE__ 的洛谷专栏和博客园中，欢迎光临。

就到这里吧，感谢你的观看。

2025.05.20 By @__CrossBow_EXE__

幸甚至哉，歌以咏志；CEXE好闪，拜谢 CEXE。

FFT 快速傅里叶变换学习笔记

文章操作

前言