专栏文章
题解:P10137 [USACO24JAN] Walking in Manhattan G
P10137题解参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @min0wq4w
- 此快照首次捕获于
- 2025/12/01 18:45 3 个月前
- 此快照最后确认于
- 2025/12/01 18:45 3 个月前
比较有意思的题。
Solution P10137
下文称“关键点”为横纵路径的交点。
不难考虑暴力。
- 每次先把奶牛从初始点挪到一个关键点。
- 根据时间开始模拟到下一个关键点(称一次这个过程为“挪一步”)。
- 最后如果剩余的时间不足以把奶牛挪到关键点就用完时间 然后输出。
会 T 飞。
考虑一头奶牛,如果它已经在一个关键点了且时间已经确定,那么它接下来的移动路径是确定的,这个显然。
进一步的,如果时间的奇偶性确定了,那么移动路径同样确定,因为你往哪边挪只与时间的奇偶性相关。
这个时候你其实可以想倍增了。因为路径确定,所以你可以设 表示 这个关键点,初始时间奇偶性为 ,挪了 步之后到哪个位置。
于是我们第二步的复杂度被降到 ,但是 MLE 了,因为你显然不可能把 的倍增数组开下来。
你再想想呢?你想想两次转向会发生什么?
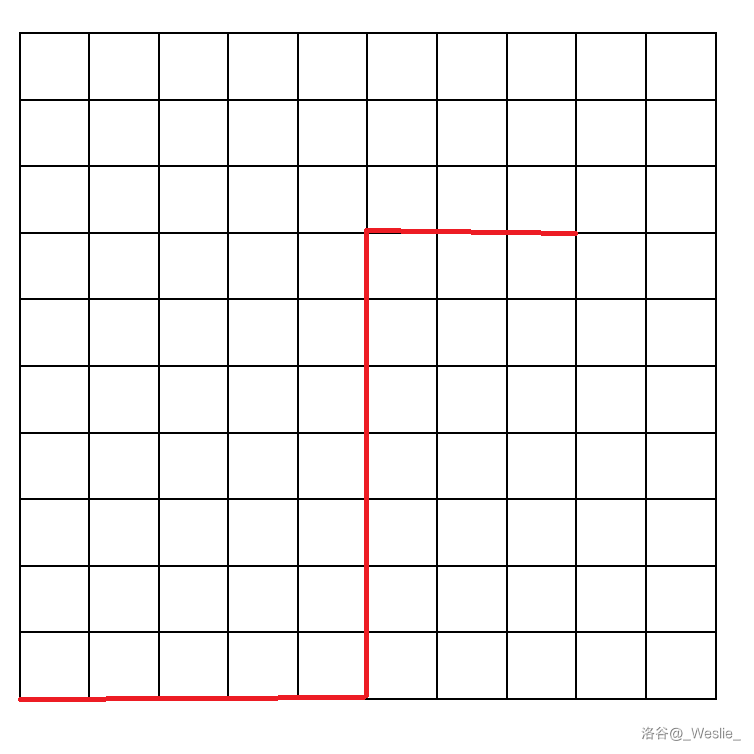
你会发现两次转向又回到了之前的方向!
而且如果我们以两次转向为一个单位考虑,行和列就可以正式被拆开了——因为你预处理倍增数组的时候,你需要保证第 行转移到的行一定会使得从第 行结束到目标行开始奇偶性变化(否则你无法走到目标行)。
然后还有一个性质:你开始走上走右,在轮数一定是 的倍数的情况下,对最终位置其实并没有影响。
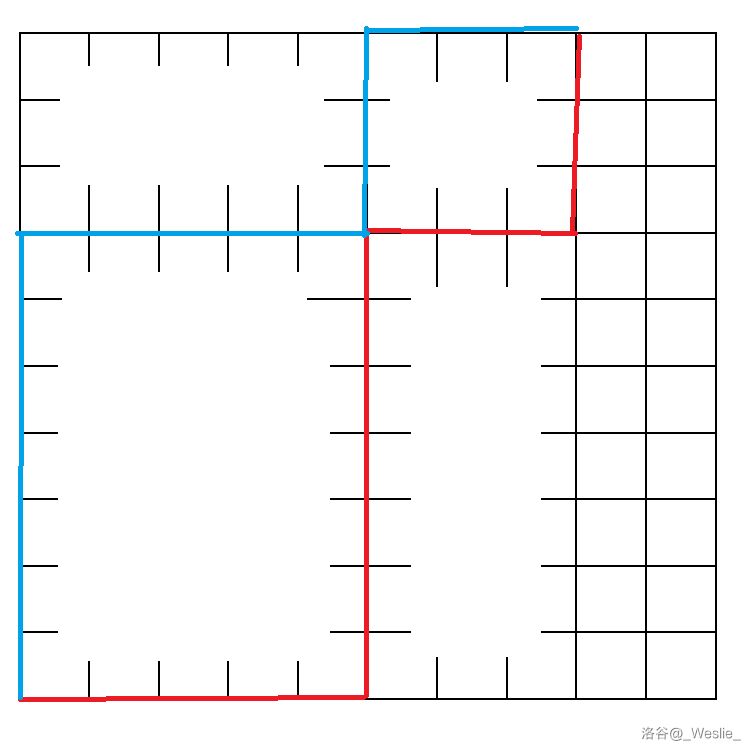
可以参考这张图上的蓝线和红线理解。
那么可以设 表示第 条竖线,连转 个两次后,到达第几条竖线; 表示第 条横线,连转 个两次后,到达第几条横线。
然后转移倍增数组就是
初值设为第一个使得两条竖线间距离差为奇数的点即可,具体上说,设 为第 和 条竖线的距离差,则:
f_{i,0}=i+1,&dis\bmod 2=0\\
f_{i,0}=f_{i+1,0},&dis\bmod 2\ne 0
\end{cases}$$
结束第二步之后你有可能剩下一部分 $t$ 还可以走,直接暴力跑就行,容易发现最多会暴力 $3$ 次。
复杂度 $\operatorname{O}(q\log n)$。代码实现较难。
::::success[Code]
```
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define fastio ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define ls (now<<1)
#define rs ((now<<1)|1)
#define int long long
using namespace std;
const int N=200005;
const int mod=1000000007;
const int intinf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
int lx[N],ly[N];
int f[N][19],g[N][19];
int n,q,lenx,leny;
pair<int,int> solve(int x,int y,int t){
pair<int,int>ans=make_pair(0,0);
int ut=0;
int px=lower_bound(lx+1,lx+lenx+1,x)-lx,py=lower_bound(ly+1,ly+leny+1,y)-ly;
if(lx[px]!=x&&ly[py]==y){
if(t<=(lx[px]-x)){
ans.fi=x+t;
ans.se=y;
return ans;
}
t-=(lx[px]-x);
ut+=(lx[px]-x);
x=lx[px];
}
if(ly[py]!=y&&lx[px]==x){
if(t<=(ly[py]-y)){
ans.fi=x;
ans.se=y+t;
return ans;
}
t-=(ly[py]-y);
ut+=(ly[py]-y);
y=ly[py];
}
for(int i=18;i>=0;i--){
int nx=f[px][i],ny=g[py][i];
int sum=(lx[nx]-lx[px])+(ly[ny]-ly[py]);
if(t>=sum){
ut+=sum;
t-=sum;
px=nx;py=ny;
}
}
x=lx[px];y=ly[py];
if(t==0){
return make_pair(x,y);
}
for(;;){
if((ut)&1){
int sum=(lx[px+1]-lx[px]);
if(t<=sum){
x+=t;
return make_pair(x,y);
}
t-=sum;
ut+=sum;
x=lx[px+1];px++;
}
else{
int sum=(ly[py+1]-ly[py]);
if(t<=sum){
y+=t;
return make_pair(x,y);
}
t-=sum;
ut+=sum;
y=ly[py+1];
py++;
}
}
return make_pair(x,y);
}
signed main(){
fastio;
cin>>n>>q;
char ch;
for(int pos;n;n--){
cin>>ch>>pos;
if(ch=='V')lx[++lenx]=pos;
else ly[++leny]=pos;
}
lx[++lenx]=mod*2;ly[++leny]=mod*2;
sort(lx+1,lx+lenx+1);
sort(ly+1,ly+leny+1);
for(int j=0;j<=18;j++){
f[lenx][j]=lenx;
g[leny][j]=leny;
}
for(int j=0;j<=18;j++){
for(int i=lenx-1;i>=1;i--){
if(j==0){
if((lx[i+1]-lx[i])&1)f[i][0]=i+1;
else f[i][0]=f[i+1][0];
}
else f[i][j]=f[f[i][j-1]][j-1];
}
for(int i=leny-1;i>=1;i--){
if(j==0){
if((ly[i+1]-ly[i])&1)g[i][0]=i+1;
else g[i][0]=g[i+1][0];
}
else g[i][j]=g[g[i][j-1]][j-1];
}
}
for(int x,y,t;q;q--){
cin>>x>>y>>t;
pair<int,int>ans=solve(x,y,t);
cout<<ans.fi<<' '<<ans.se<<'\n';
}
return 0;
}
```
::::相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...