题解：AT_agc021_d [AGC021D] Reversed LCS

很有意思的题啊！

一开始看到这个正串和反串的 $LPS$，就感觉会往回文那边靠。不过这个结论还是很厉害的：

感受一下就感觉很对，而且并不难证明这个结论，很巧妙地：

我们可以通过证明不等关系来证明它必定取等：首先由于最长回文子序列反过来还是一样的，都出现在正串和反串里，所以 $LPS\leq LCS$，其中 $LPS$ 是最长回文子序列的简称。

随后我们要证明 $LPS\geq LCS$，就可以得到 $LCS=LPS$。

考虑这个 $LCS$ 在原序列里面长成什么样，设它长度为 $k$，是原串 $T$ 中的 $T_{i_1},T_{i_2},\dots,T_{i_k}(i_1<i_2<\dots<i_k)$，以及反过来我们也能找到这个串，设为：$T_{j_k},T_{j_2},\dots,T_{j_1}(j_1>j_2>\dots>j_k)$（在 $T'$ 中的顺序是正过来的）。

我们总能找到一个位置使 $i_p<j_p$ 而 $i_{p+1}\geq j_{p+1}$，方便起见设 $i_{k+1}=\lvert T \rvert+1$ 以及 $j_{k+1}=-1$，这样保证两个串必然有个这样的交点。（画个图就好理解了）

现在，当 $i_{p+1}>j_{p+1}$ 的时候，我们很明显可以把串变成 $T_{i_1},\dots,T_{i_p},T_{j_p},\dots,T_{j_1}$，这是一个回文串；以及 $T_{j_{k}},T_{j_{k-1}},\dots,T_{j_{p+1}},T_{i_{p+1}},\dots,T_{i_k}$。都是回文序列，而且总长度是 $2k$ 啊！这意味着至少其中有一个长度为 $k$，我们就说明了 $LCS$ 肯定可以是 $LPS$。

而当 $i_{p+1}=j_{p+1}$ 的时候，我们把这个位置分给两个回文串就可以如上构造了：$T_{i_1},\dots,T_{i_p},T_{i_{p+1}},T_{j_p},\dots,T_{j_1}$，往另一个串里塞 $T_{j_{p+1}}$ 就得到了总长为 $2k$ 的两个回文串。画张图辅助理解：

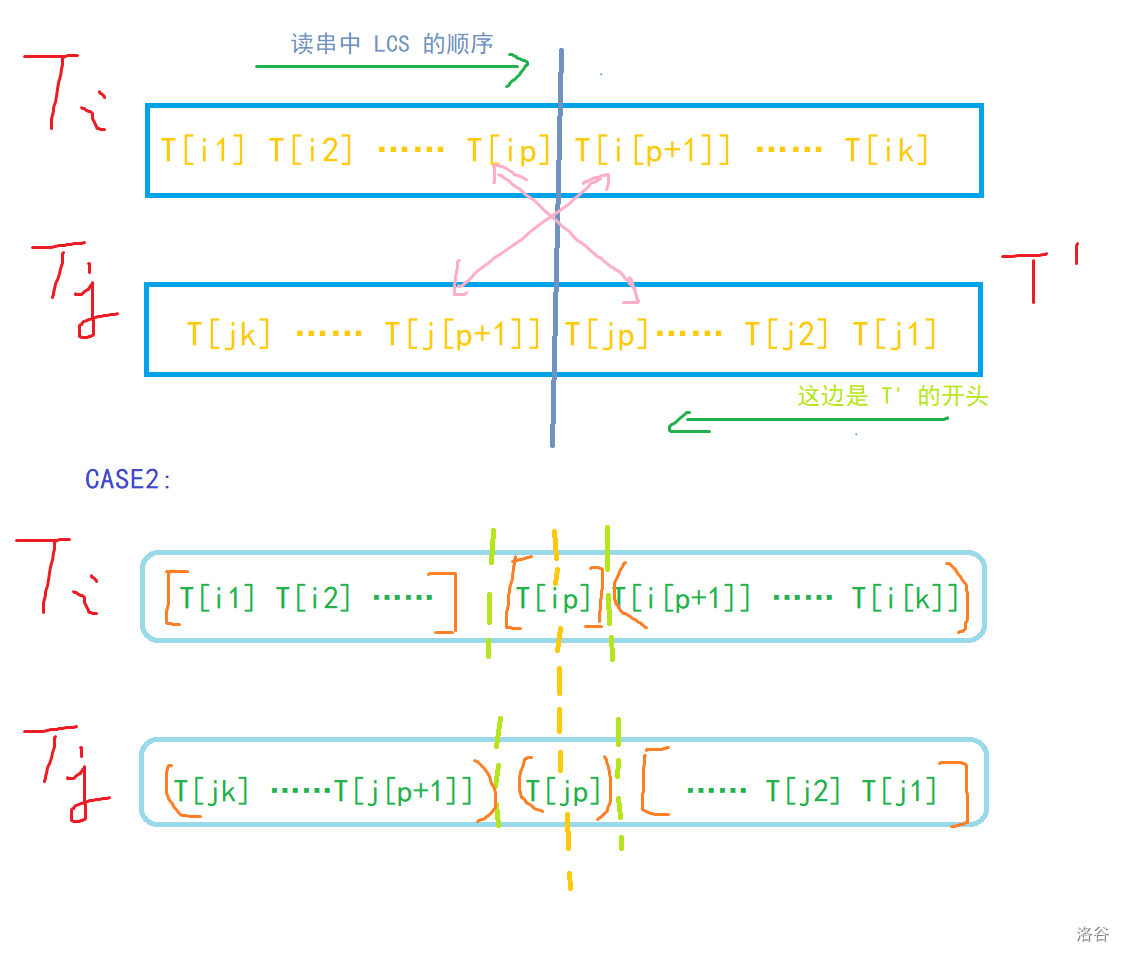
接下来问题转化为原串中最长回文子序列了，这应当是简单的，就不多说了。