专栏文章

CF2125E Sets of Complementary Sums 题解

蒟蒟蒻君HJT泽渡透香
CF2125E题解参与者 2已保存评论 5

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
5 条
当前快照
1 份
快照标识符
@mios16l3
此快照首次捕获于
2025/12/03 00:12
3 个月前
此快照最后确认于
2025/12/03 00:12
3 个月前
查看原文
∣Q∣|Q| 显然与 aa 中不同元素个数相等，不妨设值为 b[i]b[i] 的元素出现了 c[i]c[i] 次，其中 1≤i≤n,c[i]≥1,1≤b[1]<b[2]<⋯<b[n]1\leq i\leq n,c[i]\geq 1,1\leq b[1]< b[2]< \cdots < b[n]。设 QQ 中的元素是 x≥d[1]>d[2]>⋯>d[n]≥1x\geq d[1]>d[2]>\cdots >d[n]\geq 1。
考虑所有 c[i]=1c[i]=1 次的情况。此时可以发现 ∑b[i]=∑d[i]n−1\displaystyle\sum b[i]=\frac{\displaystyle\sum d[i]}{n - 1}。并且只要 ∑d[i]n−1\displaystyle\frac{\displaystyle\sum d[i]}{n - 1} 为整数且大于 d[1]d[1]，就一定能通过其分别减去所有 d[i]d[i]，来解出合法的 b[1]∼b[n]b[1]\sim b[n]。
c[i]≠1c[i]\neq 1 的情况，也可以找到类似的式子：∑b[i]c[i]=∑c[i]d[i](∑c[i])−1\displaystyle\sum b[i]c[i]=\frac{\displaystyle\sum c[i]d[i]}{(\displaystyle\sum c[i]) - 1}（怎么理解？一共有 ∑c[i]\displaystyle\sum c[i] 个数，求出 ∑c[i]\displaystyle\sum c[i] 个和，每个和对应缺掉其中一个数，所以加起来的和每个数出现了 (∑c[i])−1(\displaystyle\sum c[i]) - 1 次）。只要 ∑c[i]d[i](∑c[i])−1=d[1]+t\displaystyle\frac{\displaystyle\sum c[i]d[i]}{(\displaystyle\sum c[i]) - 1}=d[1]+t，tt 为正整数即可。
以上式子我们可以发现 d[1]d[1] 的存在是特殊的，所以将 d[1]d[1] 与其他 d[i]d[i] 分离化简，得到 d[1]+t(1−c[1])=∑i=2n(d[1]−d[i]+t)c[i]d[1]+t(1-c[1])=\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+t)c[i]，左边有上界 d[1]d[1]，右边有下界 ∑i=2n(d[1]−d[i]+1)\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)，那么是否只要满足 d[1]≥∑i=2n(d[1]−d[i]+1)d[1]\geq \displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1) 就可以了呢？确实如此，在此情况下，我们可以通过令 c[2]∼c[n]c[2]\sim c[n] 都为 11，c[1]c[1] 为 22，取合适的正整数 tt 使得 d[1]+t(1−c[1])=∑i=2n(d[1]−d[i]+1)c[i]d[1]+t(1-c[1])=\displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)c[i] 成立。
现在问题转化为了求有多少组 x≥d[1]>d[2]>⋯>d[n]≥1x\geq d[1]>d[2]>\cdots >d[n]\geq 1 满足 d[1]≥∑i=2n(d[1]−d[i]+1)d[1]\geq \displaystyle\sum_{i=2}^{n} (d[1]-d[i]+1)。注意到 d[i]d[i] 都比较接近 d[1]d[1]，记 e[i]=d[1]−d[i]+1,2≤i≤ne[i]=d[1]-d[i]+1,2\leq i\leq n，则有 2≤e[2]<e[3]<⋯<e[n]≤d[1]≤x2\leq e[2]<e[3]<\cdots <e[n]\leq d[1]\leq x。又可以转化为选出 n−1n-1 个 [2,x][2,x] 中不同的数，若他们的和为 ss，则能贡献 x−s+1x-s+1 种方案（d[1]d[1] 的方案数），因此只需要求出选出 n−1n-1 个 [2,x][2,x] 中不同的数，和为 ss 的方案数 f[s],s≤xf[s],s\leq x。先特判掉 n=1n=1 的情况（这是简单的，数组 [r,r][r,r] 的 Complementary Sum 为 {r}\{r\}）。
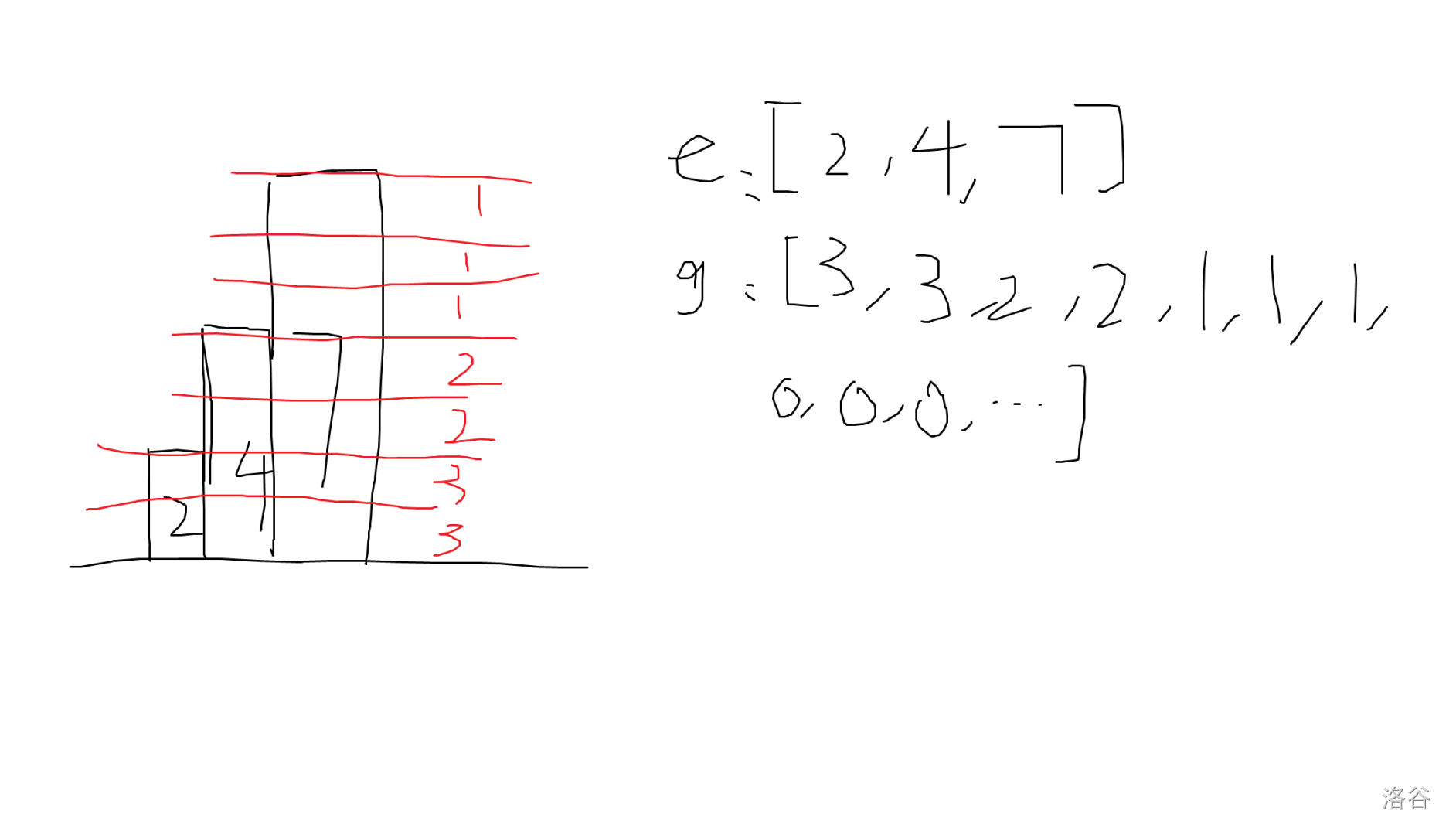
由此我们可以发现 nn 不能超过 O(x)\mathcal{O}(\sqrt x)，否则和一定超了。当然直接做背包还是做不了，因为你要记录当前的和，当前选了几个数，外面再套一层枚举 [2,x][2,x] 显然时间复杂度爆了。这里我们可以考虑做类似 Lesbegue 积分的操作，记 g[k]g[k] 表示 e[2]∼e[n]e[2]\sim e[n] 中大于等于 kk 的数的个数，则有 ∑k=1∞g[k]=∑i=2ne[i]\displaystyle\sum_{k=1}^{\infty}g[k]=\sum_{i=2}^{n}e[i]，原理见下图。
容易得到 g[1]=g[2]=n−1g[1]=g[2]=n-1，且 g[i]−g[i−1]∈{0,−1}g[i]-g[i-1]\in \{0,-1\}，这样子转化的好处是所有 g[k]g[k] 中 1∼n−11\sim n-1 必然都出现了大于等于 11 次，特别地，n−1n-1 必然出现了大于等于 22 次，而不再有选数个数的限制。依次考虑 1∼n−11\sim n - 1，每次加入一个新的 ii，令 f′[s]←f[s−i]+f[s−2i]+⋯f'[s]\leftarrow f[s-i]+f[s-2i]+\cdots 即可，实际上是一个完全背包。具体实现可以参考代码。
CPP
#include <bits/stdc++.h>

const int mod = 998244353;
int mul(int x, int y){
  return 1ll * x * y % mod;
}
int minus(int x, int y){
  x -= y;
  if(x < 0) x += mod;
  return x;
}
int add(int x, int y){
  x += y;
  if(x >= mod) x -= mod;
  return x;
}
int Qpow(int x, int y){
  int r = 1;
  while(y){
    if(y & 1) r = mul(r, x);
    x = mul(x, x); y >>= 1;
  }
  return r;
}

int n, x, f[200005], g[200005];

void solve(){
  scanf("%d%d", &n, &x);
  if(n == 1){
    printf("%d\n", x);
    return ;
  }
  int ans = 0;
  if(1ll * (n + 2) * (n - 1) / 2 > x){
    printf("0\n");
    return ;
  }
  for(int i = 0; i <= x; ++i) f[i] = g[i] = 0;
  f[0] = 1;
  for(int i = 1; i <= n - 1; ++i){
    for(int j = 0; j <= x; ++j){
      if(j < i) g[j] = 0;
      else g[j] = add(g[j - i], f[j - i]);
    }
    for(int j = x; j >= 0; --j){
      f[j] = g[j];
      if(i == n - 1 && j >= i) f[j] = minus(f[j], f[j - i]);
    }
  }
  for(int j = 0; j <= x; ++j) ans = add(ans, mul(f[j], x - j + 1));
  printf("%d\n", ans);
  return ;
}

int main(){
  int T = 1;
  scanf("%d", &T);
  while(T--) solve();
  return 0;
}

评论

共 5 条评论，欢迎与作者交流。

正在加载评论...