整理了一些关于 Splay 的资料,一个简洁美丽而高效的数据结构。
Splay 是最简洁的平衡树之一,支持维护区间信息。相比线段树,其可以动态地删点、加点,更加灵活;相比分块,其复杂度是均摊对数,更加高效。
在形态变化时,Splay 并不通过维护一系列性质来保证树高,而是通过伸展保证均摊复杂度。这让它少了常见平衡树的繁杂分讨,但常数也要大不少。
形态及操作
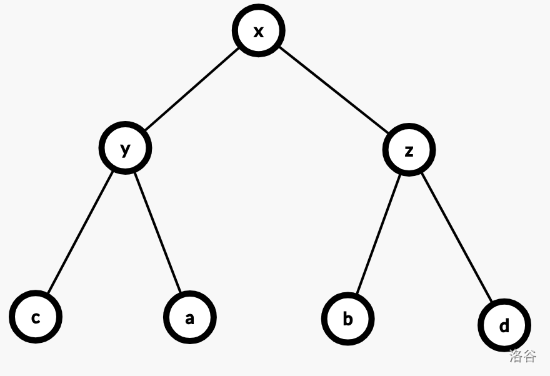
Splay 首先是一棵二叉搜索树,由许多节点组成。我们在每个节点维护父亲的左右儿子指针,以及键值。如有需要,还可以维护它子树内的信息,如它的子树大小。维护子树大小,可以实现快速查询第 k 大或者某数排名。
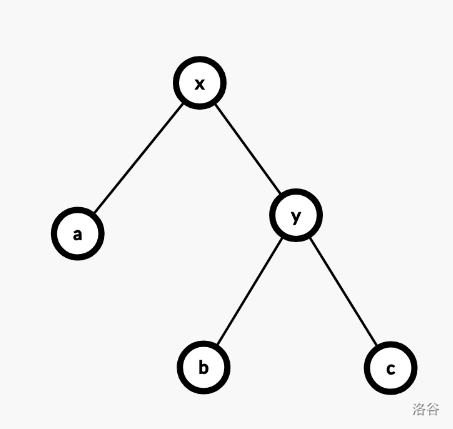
Splay 的核心操作是伸展(splay)。伸展某个节点
x,意味着将
x 节点提升到根,同时更新所维护的子树信息。原来的根在伸展后成为某个普通内部节点。伸展操作的均摊复杂度是对数。
如果能够实现伸展操作,就可以方便地进行许多操作:
-
插入。插入与普通二叉树的插入相同,按照二叉树的遍历方法找到某个叶子节点,将新值插入到该叶子的儿子下。不同的是,在插入某个点后,为了保证复杂度正确,我们要将这个节点伸展到根。
-
删除。首先将这个节点伸展到根,然后将其与其儿子断开。这时原树分裂成两个子树,考虑合并它们。找到左子树的最大值,由二叉树的性质,这个数一定小于右子树的最小值。因此,我们将
y 伸展到根。这时
y 的右儿子一定空,于是将右子树拼到其右儿子上即可。
-
查找某个数。按照二叉树的查找方法,一直找到这个数,或者某个叶子。将最后找到的节点伸展到根。
-
查询排名。首先查找这个数,伸展到根。然后小于其的数数量就是现在根左子树的大小。如果待查询的值不存在,还要考虑根是否小于这个数。
-
查询第
k 大。和二叉树相同。从根节点开始遍历。如果当前节点
x 左子树的大小,也就是小于
x 的数字数量,大于等于
k,要找的节点在左子树;如果等于
k−1,那么就是当前节点
x;否则,在右子树,并且
k 减去左子树加上当前点大小。
-
查询前驱。伸展到根,然后找左子树的最大值,也就是一直向右走。如果查询的值不存在,特判根是否小于待查值。
-
查询后继。与查询前驱同。
-
查询区间。设待查询区间为
[l,r],我们将
l−1 旋到根,
r+1 旋到根的右儿子,那么根的右儿子的左儿子,其上的信息就是
[l,r] 的信息。
伸展
旋转
现在,我们只需要有效地实现伸展操作,就可完成所需的一切操作。
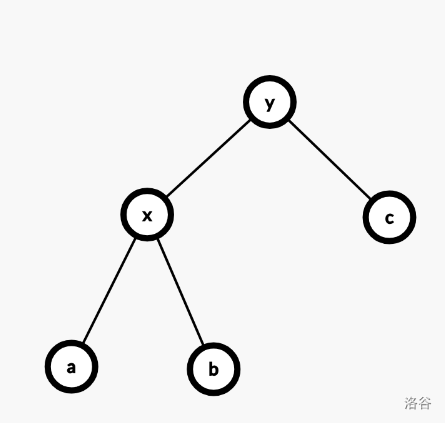
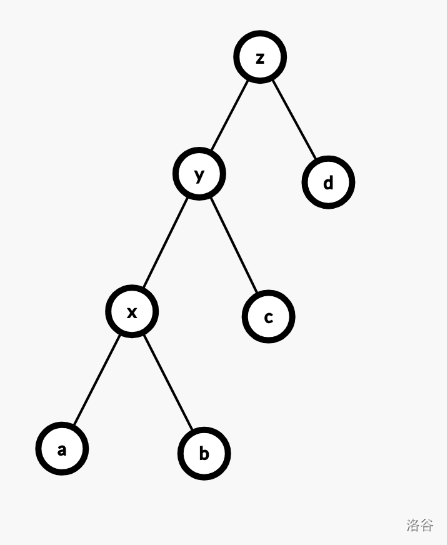
考虑怎么将某个节点高度提升一。我们称这个操作为旋转。
那样,
4 该放到哪里?可以接到
2 的右儿子上。
2 的右儿子放到哪里?放到
4 的左儿子上,因为
4 原来的左儿子是
2,现在已经空。其他子树不变。因此,变的只有
2 和
4。
单旋与双旋
伸展操作能不能直接一直向上旋转呢?可以,但复杂度错误。
为了改善复杂度,我们需要引入双旋。
双旋是指,在伸展过程中,如果出现
x 与
x 的父亲同向,不能简单地旋转两次
x,而是要先旋转其父亲,再旋转
x。
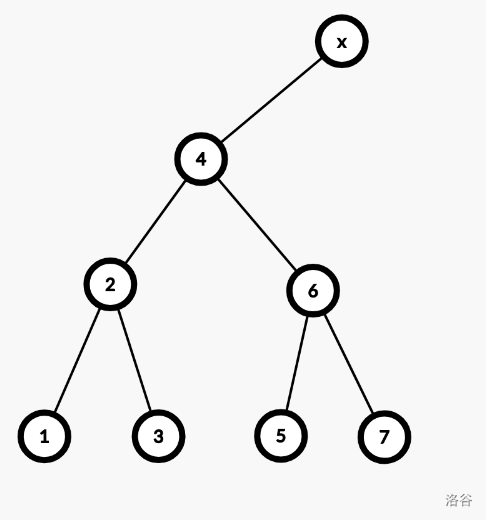
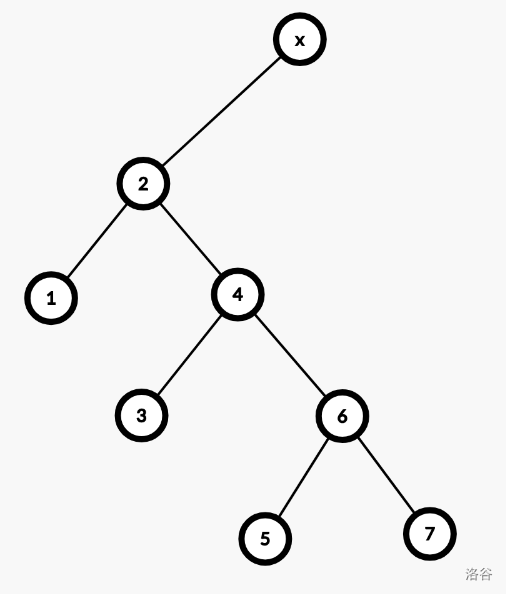
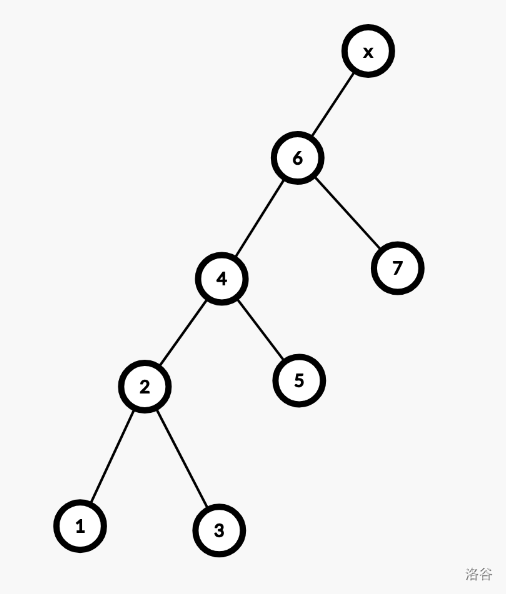
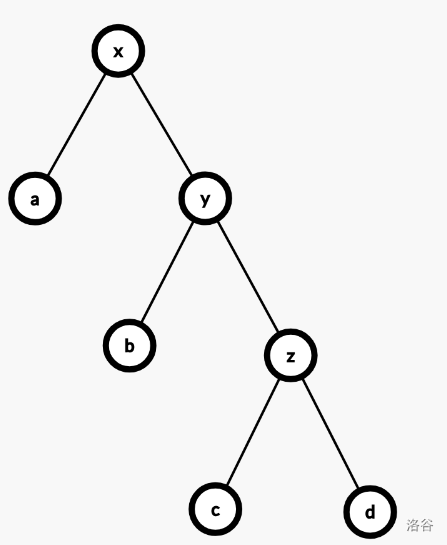
我们如果想要将
6 伸展到根,是不是需要双旋?答案是肯定的,因为
4 和
6 都是其父亲的右儿子,属于同向。如果是伸展
3,就不需要了。按照双旋的过程,我们先旋转
4,再旋转
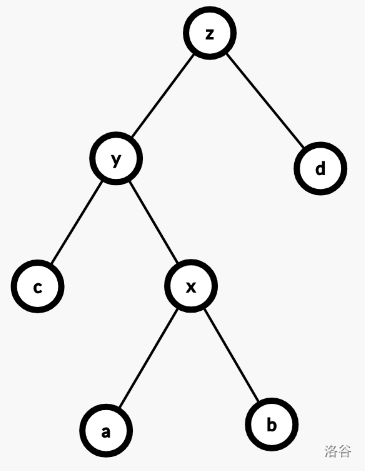
6。也就是,先变成:
光看上图,可能感觉双旋和单旋没有什么区别,但实际上在复杂度分析时,使用双旋可以保证某个性质,进而保证复杂度正确。
总之,我们已经知道了怎样以正确的复杂度将
x 伸展到根。有关 Splay 的基本操作,就介绍完毕了。
复杂度
势能分析简介
我们发现,Splay 的复杂度来源于两部分,一部分是遍历,另一部分是伸展。让最终遍历到节点马上被伸展到根,就可以把复杂度都算在伸展里,进而只需证明伸展的复杂度。
我们采用势能分析。势能分析是指,引入某个势能函数
Φ(D),描述某时数据结构的状态。
设每次操作的代价是
ci,每次操作后数据结构为
Di。要证
∑ci 有某上界。如果
Φ(Dn)−Φ(D0)=O(F(n)),
Φ(Dn)−Φ(D0)+∑ci=∑(ci+ϕ(Di)−ϕ(Di−1))=O(G(n)),显然
∑ci=O(F(n)+G(n))。
这样有什么好处?我们考虑,Splay 等数据结构复杂度分析的难处,在于我们只知道
ci 的一个很松的上界,而不好直接分析
∑ci。实际上,某个大的
ci 对数据结构的影响也是大的,会导致后续的操作
ci 更小;换句话说,不会出现所有
ci 都取到上界的情况。
引入势能函数后,每个很大的
ci,可以用一个很小的
Φ(Di)−Φ(Di−1) 来平衡。因而可以更方便地放缩,并得到上界。
具体分析
我们设某个节点的势能函数为
ϕ(x)=log∣x∣(
log 均以二为底;
∣x∣ 表示
x 的子树大小),
Φ(D)=∑ϕ(x)。显然的,
0≤Φ(D)<nlogn,并且
Φ(Dn)−Φ(D0)=O(nlogn)。我们要证明每次伸展操作的均摊复杂度是对数。
伸展的分解
根据上面对 Splay 的介绍,我们可以将伸展分为三种具体操作。设
x 为待伸展的节点,
y 为
x 的父亲,
z 为
y 的父亲。
-
zig,即一次单旋,在
y 为根时候发生。直接旋转
x,其深度减少一。发现这种旋转最多发生一次。
-
zig-zig,即一次双旋,在
y 和
x 同向时发生。先旋转
y,后旋转
x。
x 深度减少二。
-
zig-zag,即两次对
x 的单选,在
x 和
y 不同向时发生。
x 深度减少二。
伸展的过程是数次 zig-zig 与 zig-zag 的组合,加上可能存在的一次 zig。
zig 的分析
旋转的复杂度为
O(1),势能的变化量为
ϕ(x′)+ϕ(y′)−ϕ(x)−ϕ(y)=ϕ(y′)−ϕ(x)≤ϕ(x′)−ϕ(x)
因此摊还代价是
O(1)+ϕ(x′)−ϕ(x)。
zig-zig 的分析
摊还代价是
==c1+ϕ(x′)+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)−ϕ(z)1+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)
考虑怎么把
1 去掉,因为如果引入
1,就会导致最终复杂度与旋转次数有关。
有:
2ϕ(x′)−ϕ(x)−ϕ(z′)=log(∣x∣∣z′∣∣x′∣2)≥1
这是因为
∣x′∣≥∣x∣+∣z′∣。注意到不双旋时,此不等式不满足。这也是为什么双旋才能保证复杂度。
成功将常数消去,同时和前面的
ϕ(x′)−ϕ(x) 保持了一致。
zig-zag 的分析
类似的,我们有不等式:
2ϕ(x′)−ϕ(y′)−ϕ(z′)=log(∣y′∣∣z′∣∣x′∣2)≥1综合
分析得到,zig 的摊还代价为
O(1+ϕ(x′)−ϕ(x)),而这种旋转最多一次;其他的两种旋转,摊还代价都是
O(ϕ(x′)−ϕ(x))。这样,伸展的总代价就是
O(log∣x′∣−log∣x∣+1)=O(logn)。我们成功证明了伸展的复杂度是摊还对数,由此知道 Splay 的复杂度是正确的。