论 dfs 的优化：不是搜索选择优化，而是优化选择搜索

写在前面

算法竞赛中，相比于其它思想，深度优先搜索（dfs）算法起到了不可替代的作用。它没有高深的理论、冗长的证明、过于复杂的代码；但是，无论是暴力夺分、对拍验证还是人类智慧，都常有其身影。图论上，基于 dfs 的函数更是不计其数。

dfs，核心思想是“不撞南墙不回头”，可理解为迷宫求解的左手原理。即：一直将一个状态往下探索，直到状态无解或遇到正确答案。

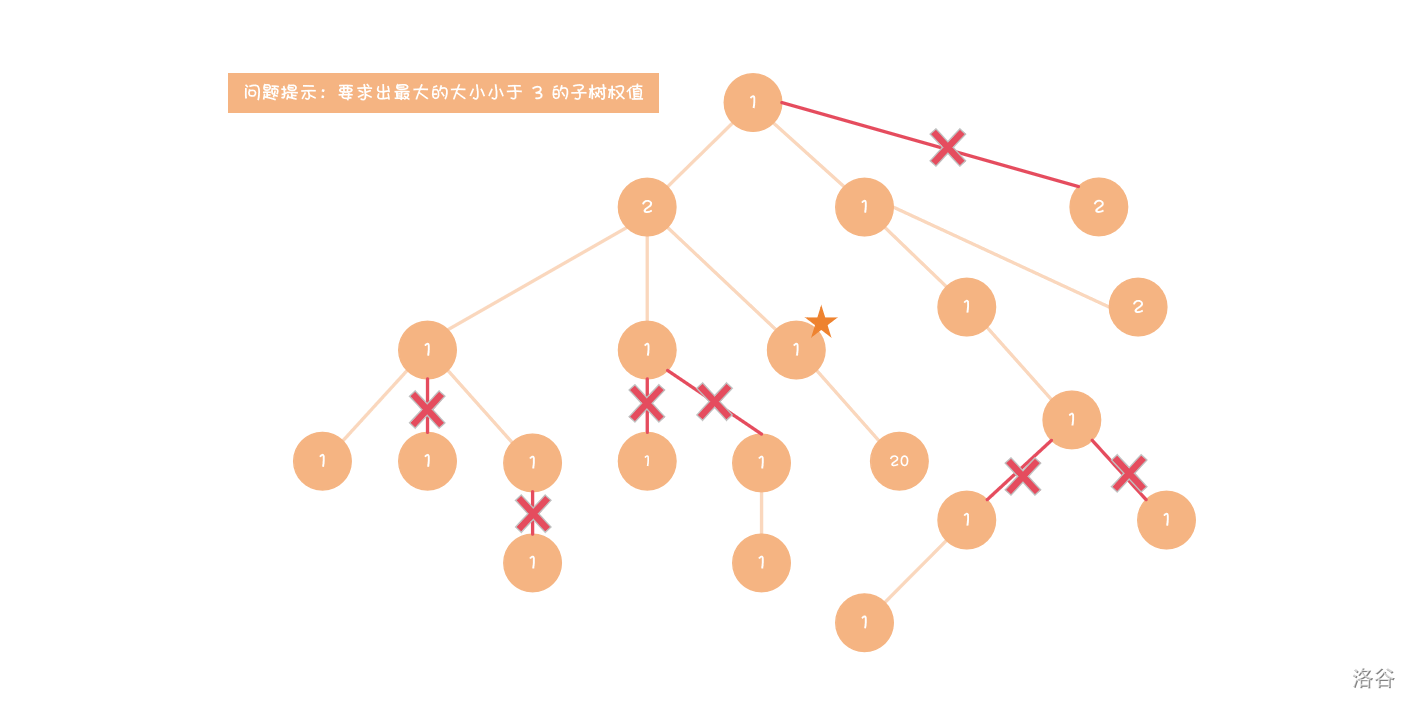
如，要在搜索树中寻找

12

号点。下图中，搜索算法会观察链条

1 \to 2 \to 3 \to 4

，并在发现

4

号为叶子无法成立后回到

3

号点，开始遍历

5,6,7

三个点。之后其又会遍历以

8

为根的子树，在发现其完全不可行后往右遍历，发现了

12

号点，即为其答案。当然，在搜索算法中往往需要父节点向子节点传递信息，信息也须回溯。

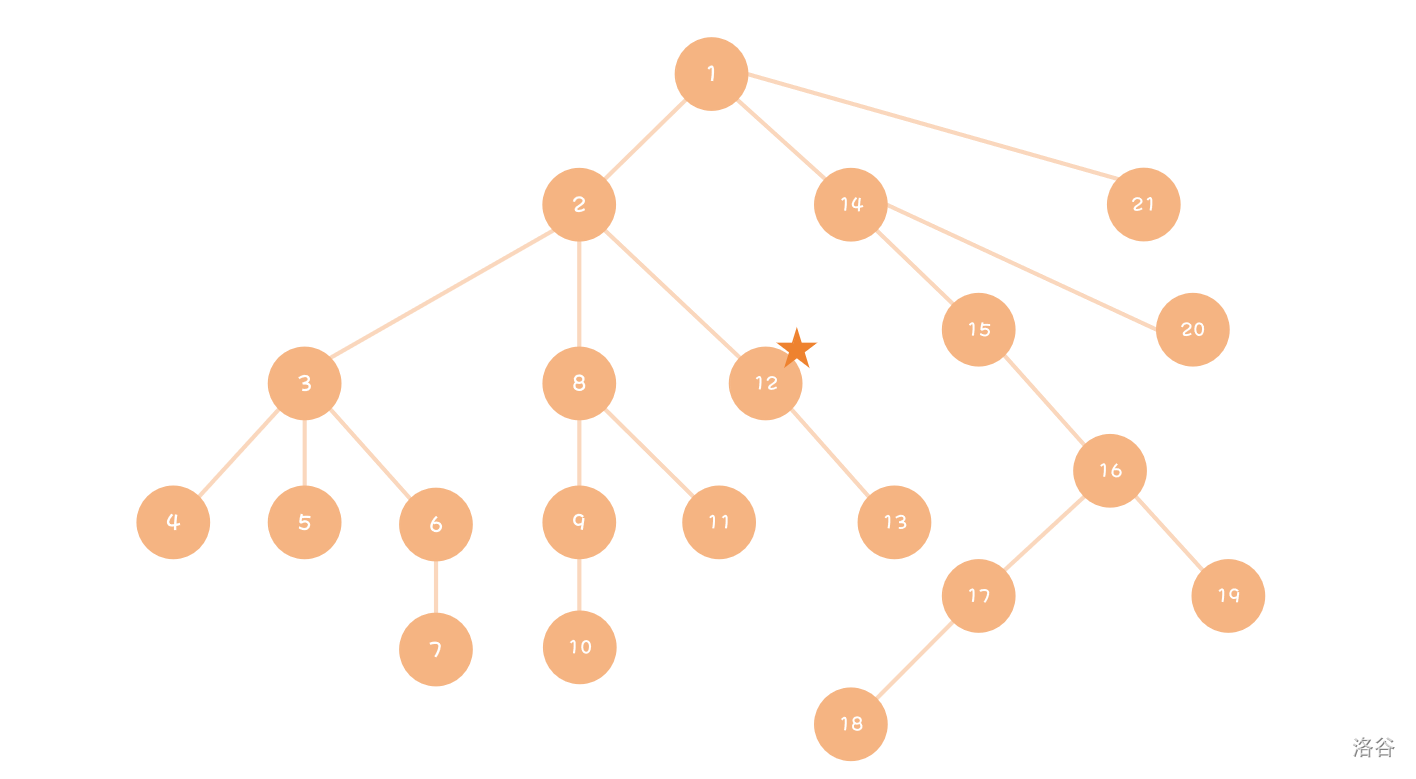
深度优先搜索算法的奥妙远没有就此结束。为了优化其高额的时间复杂度，我们需要两个利器：

减去能够确定不会产生答案的子树；（搜索剪枝）
改变 dfs 的遍历顺序。（IDDFS 和双向搜索）

两者本质不同。虽然这两种算法都不会影响答案，但是前者会导致有些点永远无法被访问，而后者不会。前者更加灵活变通，而后者不同。前者一般无法大额提升复杂度却能大额提升时间，而后者在复杂度上做出了改变。

本文将聚焦于这些优化方法，展开描述 dfs 优化的妙处。

搜索剪枝

六个字描述：删除无用子树。

搜索剪枝的方法也分

4

种，它们是：

搜索顺序重排

对顺序排序，将含有答案的枝条尽量排前面。

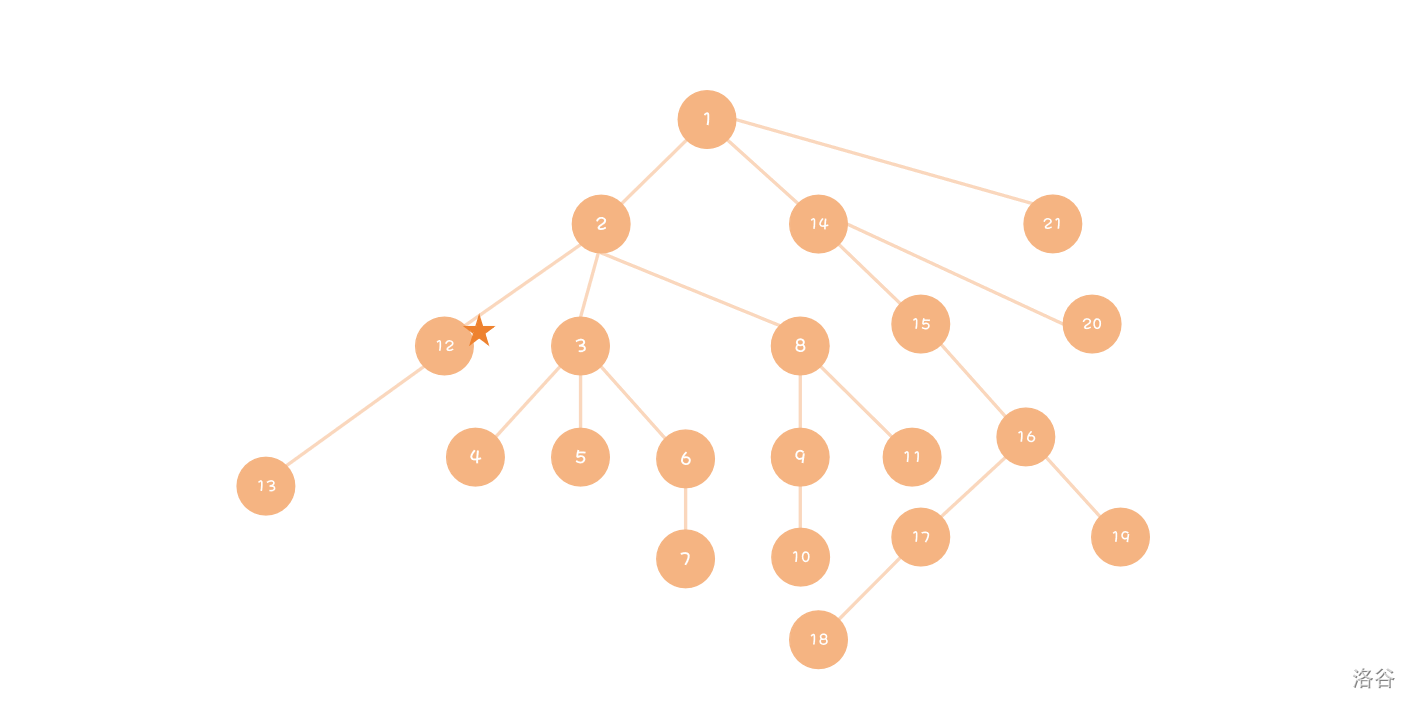
可行性剪枝

通过题意，只选取可能出现答案的枝条。

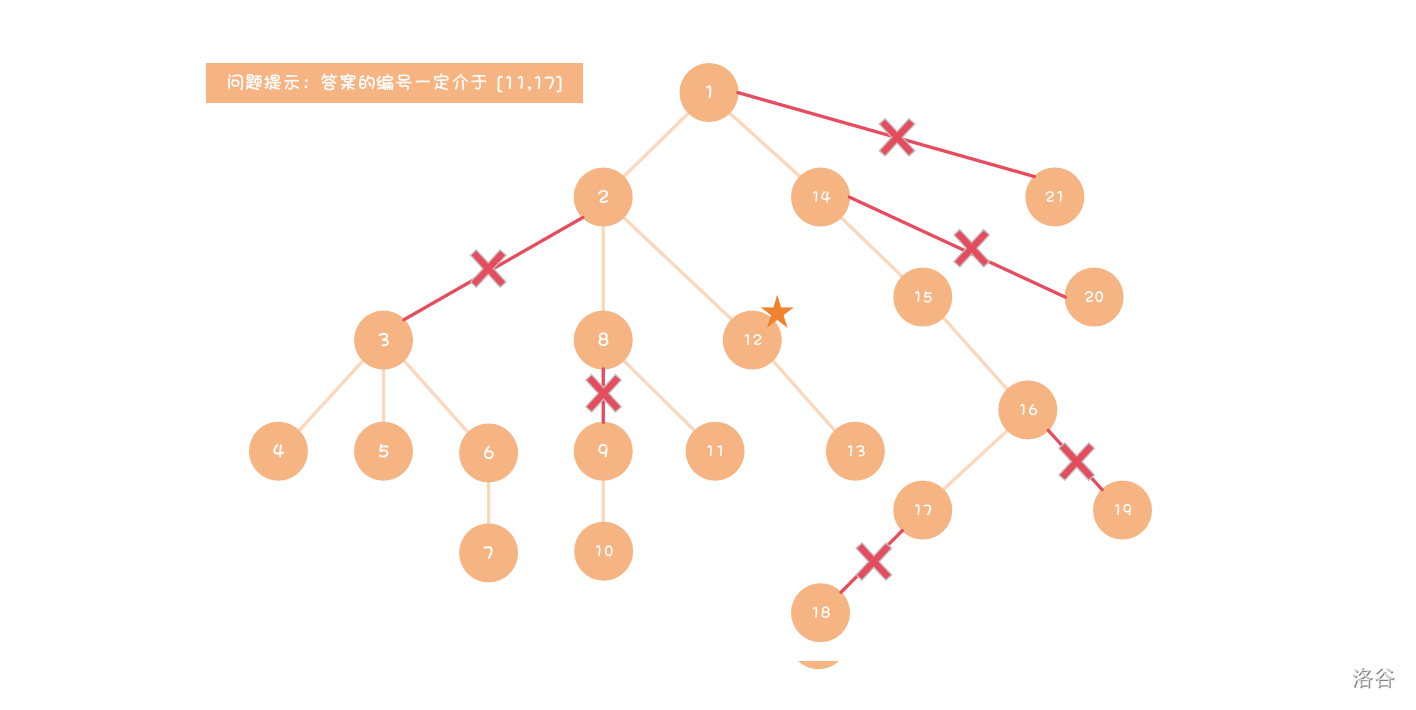
最优性剪枝

将已搜到的答案对后面产生的答案作比较，如果不可能比它更优那么直接不搜，常配合搜索顺序一起剪。

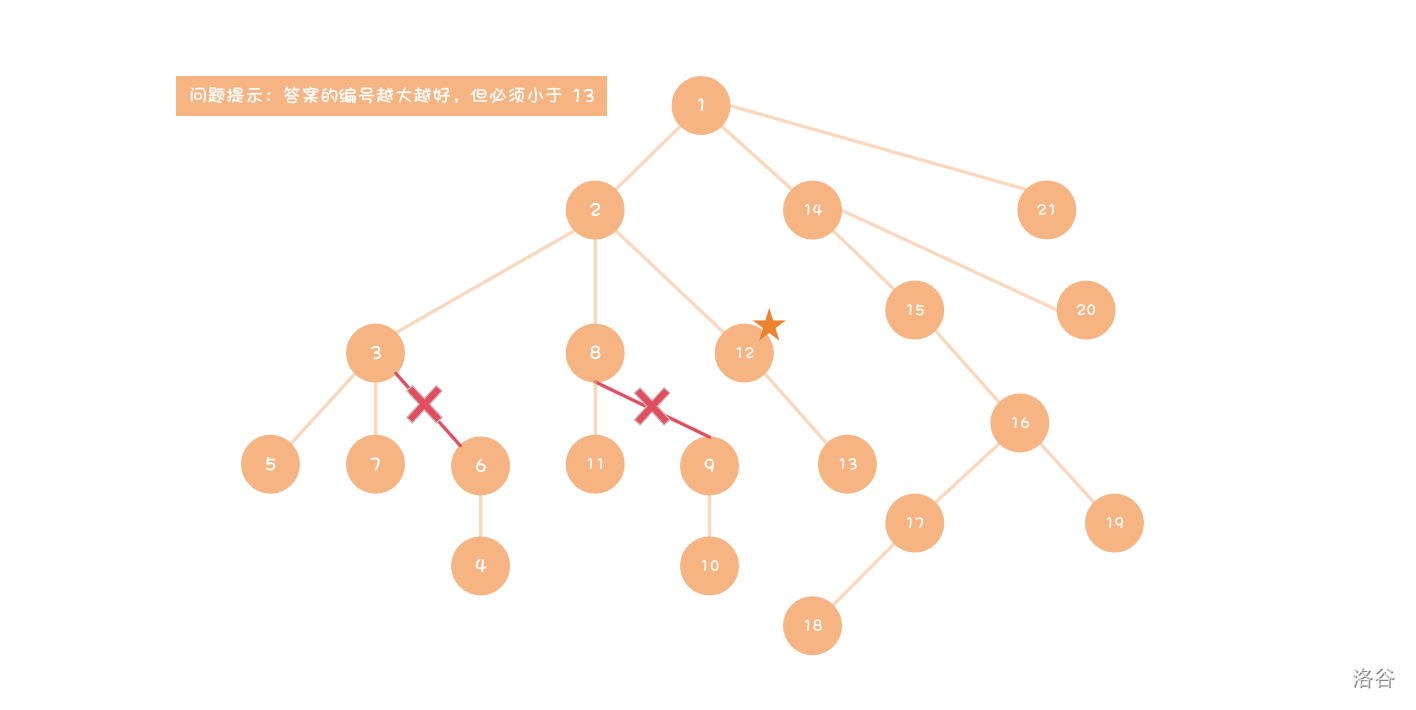
重复性剪枝

尽量减少重复的状态，以降低时间复杂度。

使用上面的四种方法，就能够做出许多问题。

例题 1

小木棍。

可以考虑成排列问题，对于每个答案，验证一次的复杂度为

n!

。

必然会超时，考虑优化每一次的 dfs：

搜索顺序：因为短木棍更灵活，所以考虑后期救场，将配对每一组时，将木棍从大到小排序。并且总值域比 $n$ 小，所以以木棍长度建立桶，直接用桶记录支持爆搜。
可行性：木棍长度之和 $\bmod$ 最终答案必须为 $0$ 。如果刚拼接好一个木棍或者加上这个木棍刚好拼完，并搜索失败，可以直接回溯。因为在用其他木棍搜下去和它们也是用那么多的木棍拼是一样的，也会失败。
最优原则：循环从小到大枚举最终答案。
降低重复运算：用从大到小的顺序保证不会重复。

代码

CPP

#include<bits/stdc++.h>
using namespace std;
int T,n,a[110],sum,x,minn=110,maxn;
bool flag;
inline void dfs(int num,int cnt,int maxm,int ans) {
	if(flag) return;
	if(num==0) {
		cout<<ans<<"\n";
		flag=1;
		return;
	}
	if(cnt==ans) {
		dfs(num-1,0,maxn,ans);
		return;
	}
	for(int i=maxm; i>=minn; i--)
		if(a[i]>0 and cnt+i<=ans) {
			a[i]--;
			dfs(num,cnt+i,i,ans);
			a[i]++;
			if(cnt==0 || i+cnt==ans) return;
		}
}
inline void solve() {
	sum=0, minn=110, maxn=0;
	flag=0;
	for(int i=1; i<=105; i++) a[i]=0; 
	cin>>n;
	if(n==0) exit(0);
	for(int i=1; i<=n; i++) {
		cin>>x;
		if(x>50) continue;
		sum+=x;
		minn=minn>x?x:minn,maxn=maxn<x?x:maxn;
		a[x]++;
	}
	int tmp=sum>>1;
	for(int i=maxn; i<=tmp; i++){
		if(sum%i==0) dfs(sum/i,0,maxn,i);
		if(flag) return;
	}
	cout<<sum<<"\n";
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	while(true) solve();
	return 0;
}

例题 2

Sudoku 2。

如果枚举每个元素的可能性并在最后判断，代码的时间复杂度为

9^{81} \approx 10^{77}

，超算都救不回来。

考虑可行性剪枝：如果填入与已有数据矛盾的数据，立即离开。不过，这仍无法解决问题。

不妨将一行、一列、或者一个方块的状态压缩到一个二进制数

v

上面，对于二进制位

\textrm{pos}

，用

1

表示不能填这个数，用

0

表示能填。

这样一来，定义

\textrm{row}_x

表示

x

所在行，

\textrm{line}_x

表示

x

所在列，

\textrm{block}_x

表示

x

所在块，令

|

表示按位与，考虑如下更新或检测方法：

若 $\textrm{row}_x~|~\textrm{line}_x~|~\textrm{block}_x$ 的第 $i$ 位为 $0$ ，则可填入 $i$ 。
若填入 $i$ ，必使 $\textrm{row}_x \gets \textrm{row}_x~|~2^i$ ， $\textrm{line}_x \gets \textrm{line}_x~|~2^i$ ， $\textrm{block}_x \gets \textrm{block}_x~|~2^i$ 。
回溯时，使 $\textrm{row}_x \gets \textrm{row}_x \oplus 2^i$ ， $\textrm{line}_x \gets \textrm{line}_x \oplus 2^i$ ， $\textrm{block}_x \gets \textrm{block}_x \oplus 2^i$ 。

此题可解...等等？

TLE 代码

CPP

#include<bits/stdc++.h>
using namespace std;
string s,ss;
inline int getR(int idx){
	return idx/9+1;
}
inline int getC(int idx){
	return idx%9+1;
}
inline int getB(int idx){
	return ((getR(idx)-1)/3)*3+(getC(idx)-1)/3+1;
}
int r[10],c[10],b[10];
bool flag;
inline void dfs(int step){
	if(flag) return;
	if(step==81){
		for(int i=0; i<81; i++) putchar(s[i]);
		putchar(10);
		flag=1;
		return;
	}
	if(ss[step]!='.'){
		dfs(step+1);
		return;
	}
	int cond=r[getR(step)]|c[getC(step)]|b[getB(step)];
	for(int i=0; i<=8; i++){
		if(cond&(1<<i)) continue;
		s[step]='1'+i;
		r[getR(step)]|=(1<<i);
		c[getC(step)]|=(1<<i);
		b[getB(step)]|=(1<<i);
		dfs(step+1);
		r[getR(step)]^=(1<<i);
		c[getC(step)]^=(1<<i);
		b[getB(step)]^=(1<<i);
	}
}
inline void solve(){
	flag=0;
	getline(cin,s);
	ss=s;
	if(s[0]=='e') exit(0);
	for(int i=1; i<=9; i++) r[i]=b[i]=c[i]=0;
	for(int i=0; i<81; i++){
		if(s[i]=='.') continue;
		r[getR(i)]|=(1<<(s[i]-'1'));
		c[getC(i)]|=(1<<(s[i]-'1'));
		b[getB(i)]|=(1<<(s[i]-'1'));
	}
	dfs(0);
}
int main(){
	while(true) solve();
	return 0;
}

/*
显然考虑直接使用位运算完成此题。对于每一个九宫格、行、或者列，考虑对其赋一个二进制权值 abcdefghi。
一旦不能填了，我们就立马设 w 为 1.将某个点所在的行、列、九宫格的权值按位与一下，就可知该位能填的元素，将这三者这一列赋值为 1 并且继续。若将这一位重新 &0，就能实现回溯。
做完了。 
*/

这题显然没那么简单。

思考我们鱼类如何做数独。我们会选择一个没有任何信息的方格，在其中随机填入

1 \sim 9

中的所有数吗？

显然不会。题目假定唯一解，意味着这样一填可能的概率是

\frac{1}{9}

。如果是一个确定的格子或者二分之一的格子，那该多好啊，后续不会浪费太多无用功。

所以，程序每次会选择一个填入数字后最有希望的格子，也是抉择最少的格子。每次虽然需要遍历一遍也就是

\mathcal{O}(n^2)=\mathcal{O}(81)

，但是这会对后面的计算过程进行指数级的化简。

AC 代码

CPP

#include<bits/stdc++.h>
using namespace std;
string s,ss;
inline int getR(int idx) {
	return idx/9+1;
}
inline int getC(int idx) {
	return idx%9+1;
}
inline int getB(int idx) {
	return ((getR(idx)-1)/3)*3+(getC(idx)-1)/3+1;
}
int r[10],c[10],b[10],ans,maxn,val,tot;
bool flag;
inline int best_cell() {
	ans=-1,maxn=999;
	for(int step=0; step<81; step++) {
		if(s[step]!='.') continue;
		val=r[getR(step)]|c[getC(step)]|b[getB(step)];
		tot=9;
		while(val) val-=(val&(-val)), tot--;
		if(tot<maxn) maxn=tot, ans=step;
	}
	return ans;
}
inline void dfs() {
	if(flag) return;
	int cond=best_cell();
	if(cond==-1) {
		flag=1;
		for(int i=0; i<81; i++) putchar(s[i]);
		putchar(10);
		return;
	}
	int cenc=r[getR(cond)]|c[getC(cond)]|b[getB(cond)];
	for(int i=0; i<=8; i++) {
		if(cenc&(1<<i)) continue;
		s[cond]='1'+i;
		r[getR(cond)]|=(1<<i);
		c[getC(cond)]|=(1<<i);
		b[getB(cond)]|=(1<<i);
		dfs();
		s[cond]='.';
		r[getR(cond)]^=(1<<i);
		c[getC(cond)]^=(1<<i);
		b[getB(cond)]^=(1<<i);
	}
}
inline void solve() {
	flag=0;
	getline(cin,s);
	ss=s;
	if(s[0]=='e') exit(0);
	for(int i=1; i<=9; i++) r[i]=b[i]=c[i]=0;
	for(int i=0; i<81; i++) {
		if(s[i]=='.') continue;
		r[getR(i)]|=(1<<(s[i]-'1'));
		c[getC(i)]|=(1<<(s[i]-'1'));
		b[getB(i)]|=(1<<(s[i]-'1'));
	}
	dfs();
}
int main() {
	while(true) solve();
	return 0;
}

/*
显然考虑直接使用位运算完成此题。对于每一个九宫格、行、或者列，考虑对其赋一个二进制权值 abcdefghi。
一旦不能填了，我们就立马设 w 为 1.将某个点所在的行、列、九宫格的权值按位与一下，就可知该位能填的元素，将这三者这一列赋值为 1 并且继续。若将这一位重新 &0，就能实现回溯。
做完了。
*/

IDDFS

六个字描述：限制搜索深度。

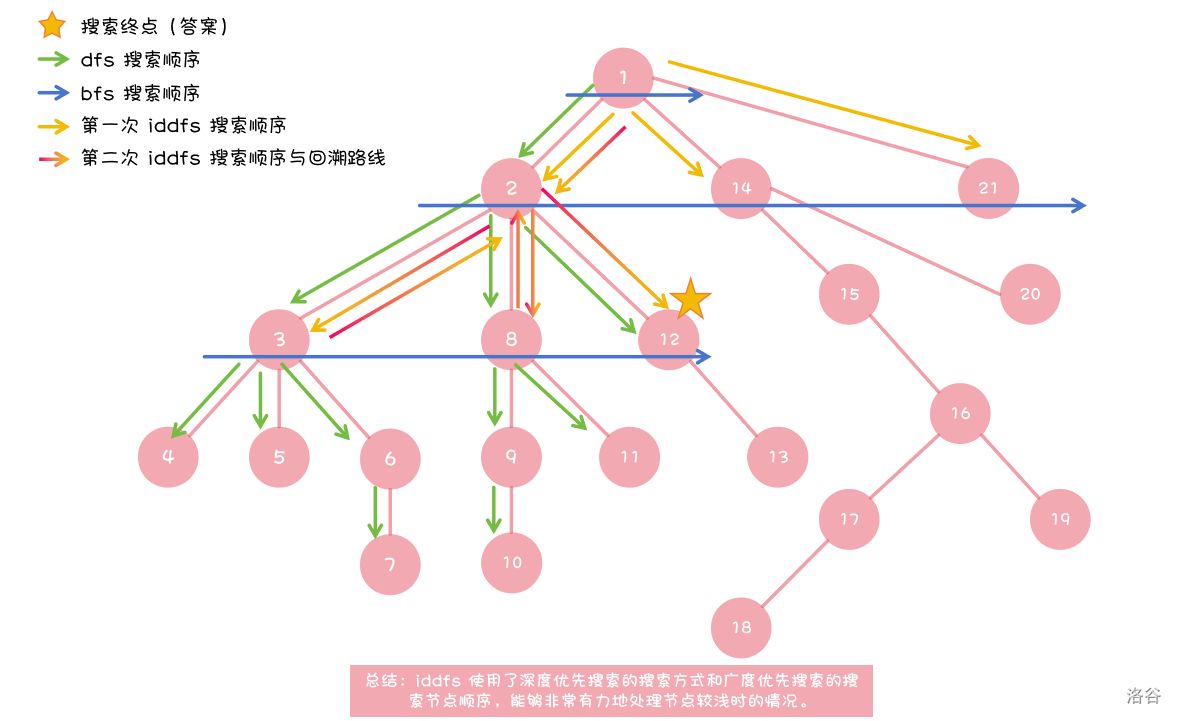
仍然观察下面这张图：

你会发现搜索者在左侧的树上做了一段时间的无用功。如果整棵树往左边倾斜，那么搜索的消耗将会巨大，栈空间可能爆表。故，在答案

\textrm{dfn}

序出现较晚时，普通的 dfs 会有一定的劣势。

除了剪去枝干之外，我们还可以尝试改变其的搜索顺序。不妨像 bfs 那样，一层、一层地搜索，这样能够解决较浅的答案。可惜的是，bfs 同样存在劣势：它的队列所需存储的元素个数很多，可能会爆空间。

一个 TLE 一个 MLE，那有没有折中的方法呢？

迭代加深搜索（Iterative Deepening DFS, IDDFS）结合了 DFS 的空间优势和 BFS 的“按层搜索”优势。

其核心思想是：从小到大，逐步放宽搜索深度的限制

\textrm{maxd}

。对于每一个深度限制，执行一次深度受限的 DFS。如果在本层找到了答案，则立即返回；否则，增加深度限制，重新开始一次全新的 DFS。

虽然看起来每一层都会重复搜索浅层节点，但因为在搜索树中，深层节点数量占压倒性多数，所以这种重复带来的额外开销相对很小。其时间复杂度与目标深度所在的 BFS 同阶，而空间复杂度仍与 DFS 同阶。

为什么一定是迭代加深搜索？

迭代加深搜索相比于深度优先搜索（dfs）来说，主要特长是一定可以搜索到相对浅层的答案，劣势是会多搜索浅层元素几遍。
相比于广度优先搜索（bfs）来说，其唯一特点就是不必使用队列存储当前状态，来赢得较低的时间复杂度。

一般需要迭代加深搜索的题目都会公示答案范围或深度，如【保证移动数量不超过

17

】。

例题 3

Power Hungry Cows。

考虑到记录下

k_1=\log_x \textrm{MV1}

和

k_2=\log_x \textrm{MV2}

，则其开始时满足

k_1=1

，

k_2=0

，每次可以进行如下操作：

$k_1 \gets 2 \times k_1$
$k_1 \gets 2 \times k_2$
$k_1 \gets k_1+k_2$
$k_1 \gets |k_1-k_2|$
$k_1 \gets 0$
$k_2 \gets 2 \times k_1$
$k_2 \gets 2 \times k_2$
$k_2 \gets k_1+k_2$
$k_2 \gets |k_1-k_2|$
$k_2 \gets 0$

直接考虑 IDDFS，最大深度则设置为至少需要多少次变换才能达到效果。

我们还可以进行一些小剪枝：

最优性剪枝：如果 $k_1 > 2 \times n$ 或者 $k_2 > 2 \times n$ ，立即停止，因为这一定是无用功。
可行性剪枝 A：考虑一个变量 $k=a$ ，则在 $b$ 轮后该变量通过自我累加能获得值 $a \times 2^b$ 。如果在限定轮数结束后都没能使 $k \ge n$ ，则在该状态下一定无解，可以剪去。这里能够证明更大的变量自我迭代产生的结果注定最大，所以取 $k=\max\{k_1,k_2\}$ 。能够发现的是：通过 IDDFS 的算法特色，其能与各种各样的剪枝联用，尤其是可行性剪枝。
可行性剪枝 B：注意到当 $k_1$ 与 $k_2$ 无论怎么互相加减，根据余数的加减性，其产生的结果除 $\gcd(k_1,k_2)$ 的余数一定等于 $0$ 。因此，易证得当 $n \bmod \gcd(k_1,k_2) \neq 0$ 时，该思路一定无解，可以舍去。

这样一来，此题可解。

代码

CPP

#include<cstdio>
int n,mxdep;
inline int gcd(int A,int B){
	return B?gcd(B,A%B):A;
}
inline bool dfs(int x,int y,int mxdep,int dep) {
	if(x>n*2 or y>n*2) return 0;
	if(dep>mxdep) return 0;
	if(x<y) x^=y^=x^=y;
	if((x<<(mxdep-dep))<n) return 0;
	if(x==n or y==n) return 1;
	if(gcd(x,y)!=0 and n%gcd(x,y)!=0) return 0;
	if(dfs(x+y,x,mxdep,dep+1)) return 1;
	if(dfs(x-y,y,mxdep,dep+1)) return 1;
	if(dfs(x-y,x,mxdep,dep+1)) return 1;
	if(dfs(x+y,y,mxdep,dep+1)) return 1;
	if(dfs(x+x,x,mxdep,dep+1)) return 1;
	if(dfs(x+x,y,mxdep,dep+1)) return 1;
	if(dfs(y+y,x,mxdep,dep+1)) return 1;
	if(dfs(y+y,y,mxdep,dep+1)) return 1;
	return 0;
}
signed main() {
	scanf("%d",&n);
	while(!dfs(1,0,mxdep,0)) mxdep++;
	printf("%d",mxdep);
	return 0;
}

例题 4

埃及分数。

这下难了，因为埃及分数的拆分是无穷无尽的。如果不限制分数的个数，极有可能引发陷入死胡同的尴尬。倘若设计阈值

\textrm{limit}

，当答案大于

\textrm{limit}

时自动返回，尚有一定风险：因为

\textrm{limit}

的值必须要设的既不大又不小，这个枝叶剪的，当然很麻烦。并且，还有 hack。

所以，可以让程序自动调节

\textrm{limit}

，也就是 IDDFS。因此，我们还可以理解到 IDDFS 是带自调节阈值的智能剪枝算法。不妨让

\textrm{maxd}

等于最多选择的分数个数，就能让程序根据输入数据智能的进行调节。

可是，第二个问题也出现了：分母也可以是无限的。那怎么办呢？那就是，可以将分母也进行迭代加深，也就是双迭代加深法。在树上遍历时，两个苛刻的条件限制，就可以达成防止 dfs 脱轨的情况下找出浅层答案的作用了。

最后，再说两个剪枝。

可行性剪枝 A：当已经累加的和 $> \frac{a}{b}$ 时，一定无解。这很好理解。
可行性剪枝 B：题解区中通过证明方程 $\frac{a}{b}=\frac{1}{x}+\frac{1}{y}$ 的判别式 $\Delta$ 得到枚举下界 $\lfloor \frac{4b}{a^2} \rfloor+1$ ，不过不在本文涉及范围之内，可做了解。

此题可解。

代码

CPP

#include<vector>
#include<cmath>
#include<algorithm>
#include<cstdio>
#define int long long
int memo[105];
std::vector<int> vec;
int nowp,cnt,max_dep=1,lim;
inline void dfs(int step,int a,int b,int pre) {
	if(!a) return;
	int tool=std::__gcd(a,b);
	a/=tool,b/=tool;
	if(step==max_dep-1) {
		for(int k=4*b/(a*a); k*a<=2*lim; k++) {
			int del=(k*k*a*a)-(4*k*b),x,y;
			if(del<=0) continue;
			int s=sqrt(del);
			if(s*s!=del) continue;
			y=((k*a)+s)>>1;
			x=((k*a)-s)>>1;
			if(x>lim or y>lim or x<0 or y<0) continue;
			if(cnt==0 or y<memo[max_dep]) {
				if(x==vec[step-1]) continue;
				for(int i=1; i<step; i++) memo[i]=vec[i];
				memo[step]=x;
				memo[step+1]=y;
				cnt=max_dep;
				break;
			}
		}
		return;
	}
	for(int i=pre+1; i<lim; i++) {
		if(a*i<b) continue;
		if((max_dep-step+1)*(1/double(i))<double(a)/double(b)) break;
		vec.push_back(i);
		dfs(step+1,a*i-b,i*b,i);
		vec.pop_back();
	}
}
int a,b;
signed main() {
	scanf("%lld %lld",&a,&b);
	while(true) {
		++max_dep;
		for(lim=1000; lim<=10000000; lim*=10) {
			for(int i=0; i<105; i++) memo[i]&=0;
			vec.clear();
			vec.push_back(0);
			nowp=cnt=0;
			dfs(1,a,b,0);
			if(cnt) {
				for(int i=1; i<=cnt; i++) printf("%lld ",memo[i]);
				return 0;
			}
		}
	}
	return 0;
}

双向搜索

六个字描述：统计多向答案。

当搜索的起点和终点都明确时，从起点和终点同时开始搜索，在中途相遇，可以极大地减少搜索空间。时间复杂度通常从

\mathcal{O}(b^d)

降为

\mathcal{O}(b^{d/2})

，其中

b

是分支因子，

d

是深度。

双向搜索的实现通常有两种方式：

双向 BFS：更适合求最短步数。两个队列交替扩展，用哈希表记录每个状态是从起点还是终点访问的，相遇时步数相加。
双向 DFS（Meet in the Middle）：更适合处理状态庞大但深度较浅的问题，尤其是组合枚举问题。从起点和终点各搜索一半深度，将产生的状态分别存储，最后通过匹配（如排序后双指针）来组合答案。

本文介绍的主要是后者：双向 DFS。

对于一棵搜索树来说，双向 DFS 将一棵搜索树一分为二并且彻底改变其结构，并最后跨树统计答案，如图所示。

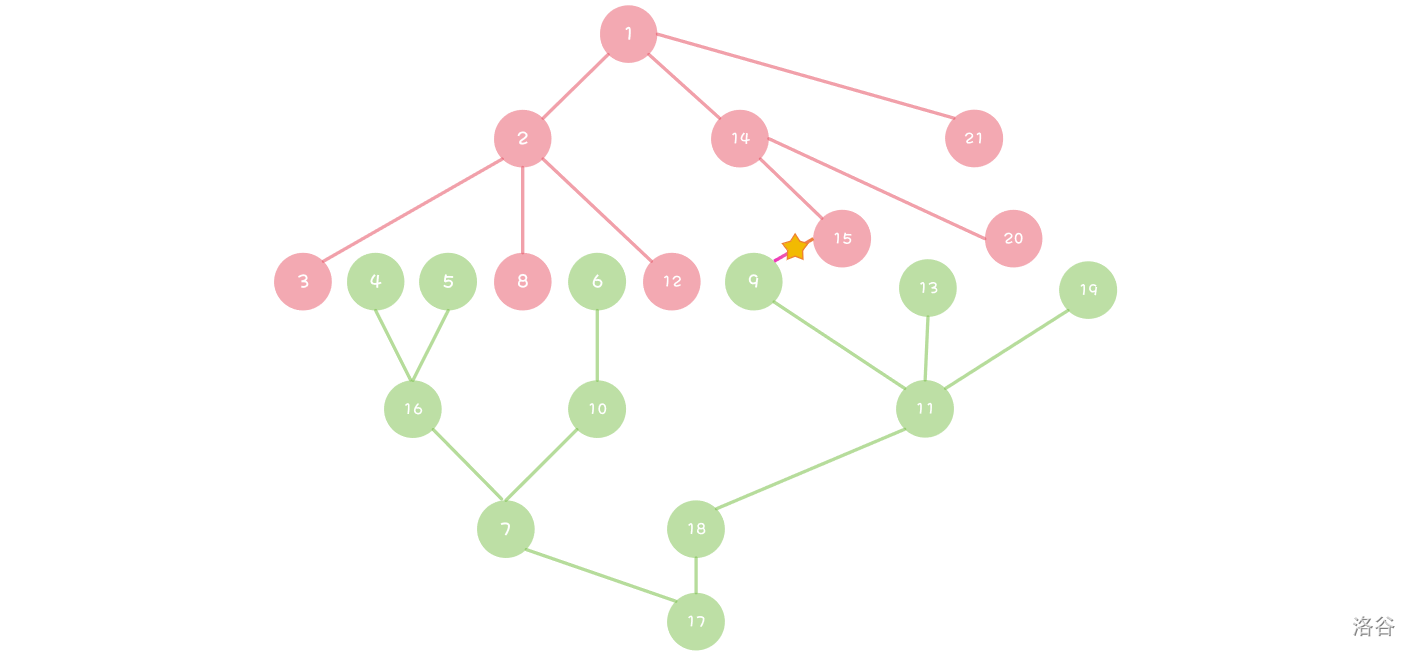
这么说你肯定还是很晕。所以看几道题。

例题 5

送礼物。

倘若直接枚举每个元素选或不选并加上适量的剪枝，最坏时间复杂度为

2^n

。由于

n=46

，所以

2^{46} \approx 10^{13}

肯定做不了。由于

W < 2^{31}

，所以第二反应动态规划也做不了。

思考这样的问题：如果有两个单调不降序列

a

或者

b

，你需要从里面选出各一个数并且这个数不小于

W

，那么该怎么做？尺取法。只需要

a

中指针一直往右走，

b

中指针找到第一个符合

b_j+a_i \le W

的值并让

a

中指针继续移动即可。时间复杂度

\mathcal{O}(\textrm{len}_a)

。

那么这和此题有什么关联呢？不妨将数组左侧部分

G_{1} \sim G_{\lfloor \frac{n}{2} \rfloor}

和数组右侧部分

G_{\lfloor \frac{n}{2} \rfloor+1} \sim G_n

分别跑一次 dfs，求出所有可能的答案（皆分布在二叉搜索树的叶子部分）。这两个答案组合，一定能够不重不漏统计出所有满足条件的礼物质量总和，而总时间复杂度为

\mathcal{O}(2 \times b^{d/2}) = \mathcal{O}(2^{24}) \approx 10^7

，此题可解。

我们能够发现：一旦找到了高效统计跨串答案的思路，就可以考虑将串切成两半，并分半求解。也就是说， $2^{46}$ 变为两个 $2^{23}$ 的搜索树缩水过程和两个搜索树叶子上的答案统计，就是 Meet in the Middle 算法的精华。

代码

CPP

#include<bits/stdc++.h>
#define ub upper_bound
using namespace std;
inline int read(){
    int s=0,f=1; char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();} // 如果是标点或负号
    while(isdigit(ch)){s=(s<<3)+(s<<1)+ch-'0';ch=getchar();} // 如果是数字
    return s*f;
}
int w,a[50],n,ans,b[(1<<24)],tot;
void getsum(int step,int sum){
    if(step==n/2+1){
        b[++tot]=sum; 
        return;
    } 
    getsum(step+1,sum);
    if(a[step]<=w-sum) getsum(step+1,sum+a[step]);
}
void dfs(int step,int sum){
    if(step==n+1){
        ans=max(ans,b[ub(b+1,b+tot+1,w-sum)-b-1]+sum);
        return;
    }
    dfs(step+1,sum); 
    if(a[step]<=w-sum) dfs(step+1,sum+a[step]);
}
signed main(){
	w=read(); n=read();
    for(int i=1; i<=n; i++) a[i]=read();
    sort(a+1,a+n+1); 
    getsum(1,0); 
    sort(b+1,b+tot+1); 
    dfs(n/2+1,0);
    printf("%lld",ans);
	return 0;
}

例题 6

Prime Gift。

第一反应竟然是完全背包，因为题意可以转化为“给你若干个数，每个数可以选无限次，问其乘积的

k

大值”。但是结果可能很大，所以数组存不下，没法做。

根据前面的经验我们可以猜出此题的技巧：将前面

p_{1} \sim p_{\lfloor \frac{n}{2} \rfloor}

的部分算出所有可能乘积，并将后面

p_{\lfloor \frac{n}{2} \rfloor+1} \sim p_n

照样算出所有可能的乘积。我们设两个答案为

\{f\}

和

\{g\}

吧。

那么怎么统计答案？考虑二分查找。通过二分查找，我们可以得知一个数大于多少个乘积（还是用类似的方法），记其为

r

。故可以让

r

接近

k

，并查出答案。

此题可解。

代码

CPP

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[30],k;
int e[5000010],g[5000010];
int tot,cnt;
void dfs1(int x,int u) {
	if(x>n) {
		e[++tot]=u;
		return;
	}
	for(int i=1; ; i*=a[x]) {
		if(1e18/i<u) break;
		dfs1(x+2,u*i);
	}
}
void dfs2(int x,int u) {
	if(x>n) {
		g[++cnt]=u;
		return;
	}
	for(int i=1; ; i*=a[x]) {
		if(1e18/i<u) break;
		dfs2(x+2,u*i);
	}
}
bool check(int x) {
	int ans=0;
	for(int i=1,j=cnt; i<=tot; i++) {
		while(j>0 and g[j]>x/e[i]) j--;
		ans+=j;
	}
	return ans<k;
}
signed main() {
	cin>>n;
	for(int i=1; i<=n; i++) cin>>a[i];
	cin>>k;
	sort(a+1,a+n+1);
	dfs1(1,1);
	dfs2(2,1);
	sort(e+1,e+tot+1);
	sort(g+1,g+cnt+1);
	tot=unique(e+1,e+tot+1)-e-1;
	cnt=unique(g+1,g+cnt+1)-g-1;
	int l=0,r=1e18,ans;
	while(l<=r) {
		int mid=l+r>>1;
		if(check(mid)) l=mid+1;
		else r=mid-1,ans=mid;
	}
	cout<<ans;
	return 0;
}

也许是巧合？

这两道题怎么长得都好像背包？难道说折半搜索的精髓在于背包？

但是好像没有发现必要联系。也许，背包更好统计串间信息。也许，我更喜欢背包。

什么时候使用双向搜索？

小心，因为不能在任何时候都使用双向搜索。双向搜索需要统计的答案是

\mathcal{O}(b^{\frac{d}{2}})

阶的。一旦跨块的信息统计达到了平方复杂度以上，其时间复杂度就会大于

\mathcal{O}(b^d)

，也就是不如不用双向搜索。

写在后面

dfs 能被如此多的算法或思想优化，不仅体现其兼容性，更体现其重要性。我们能从多种搜索剪枝算法的迥然不同看出其多样性，能从 IDDFS 的自我扩容中看出其智能性，也能从 Meet in the Middle 的砍半分治中看出其灵活性。这些一个又一个思想，归根到底，都阻止了 dfs 陷入死胡同的境地。

也许生活中，我们就像没有剪枝的深度优先搜索。答案就在眼前，只不过我们没有注意观察，而是选择撞上南墙。别担心，当下次看到

n \le 30

时，我们再也不必在算法选择的搜索树上迷茫——你应当自信一笑，在一片空白的编译软件上写下第一个函数——dfs。

论 dfs 的优化：不是搜索选择优化，而是优化选择搜索

文章操作

写在前面

搜索剪枝

例题 1

例题 2

IDDFS

例题 3

例题 4

双向搜索

例题 5

例题 6

写在后面

相关推荐

评论

论 dfs 的优化：不是搜索选择优化，而是优化选择搜索