专栏文章

题解：P5490 【模板】扫描线 & 矩形面积并

IICU_midway_azuma
P5490题解参与者 2已保存评论 1

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
1 条
当前快照
1 份
快照标识符
@miogzki3
此快照首次捕获于
2025/12/02 19:03
3 个月前
此快照最后确认于
2025/12/02 19:03
3 个月前
查看原文
前排提醒：本题要求先掌握线段树和离散化。

算法介绍：

扫描线，顾名思义，一段线在平面上扫。一般用于解决图形的周长和面积问题。
给一张动图（引用自 oiwiki）：
观察整个过程不难看出，我们实际上可以这么求图形的面积：
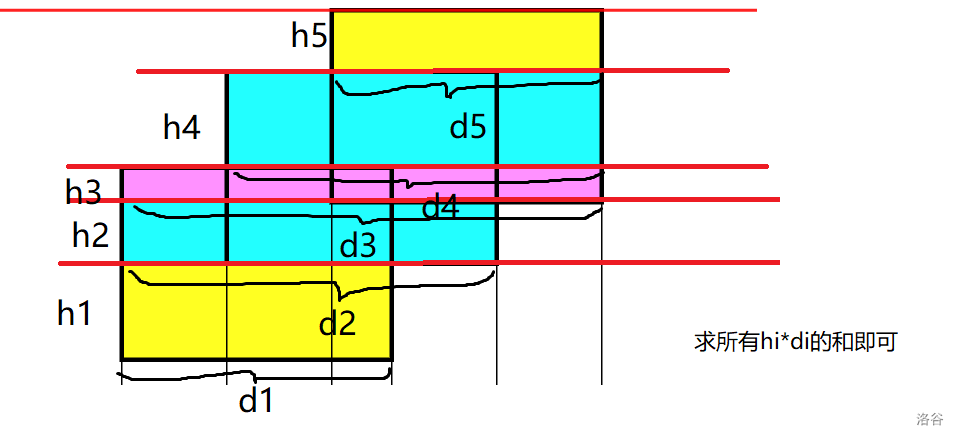
即，用一条红线不断扫描，把整个图形分成不同的小矩形，扫过的距离为小矩形的高，只需要知道每个小矩形的宽就能求得整个图形的面积。
如何求得小矩形的宽？
如果遇到矩形下方的边，就将该线段所代表的区间加一，如果是矩形上方的边就减一。
最后，数轴上大于零的位置证明被覆盖，需要计算，而等于零就证明没有被覆盖，显然不能小于零（可以看看动图中的 cntcnt 数组）。得到所有大于零的位置覆盖的总区间长度后，我们也就得到了要求的小矩形的宽（实际上矩形的说法并不严谨，但通过平移，要求的每个小形状可以等价于一个矩形）。
而我们要求得每个矩形的宽，所需要做的事情等价于两个操作：
  1. 区间加减；
  2. 统计该数组上有多少位置不为 00。
用线段树维护即可。
然后我们注意到数据范围达到了 10910^9，所以还需要离散化。

复杂度证明：

如果使用 map 离散化的话，所需的时间复杂度为 O(nlog⁡n)O(n\log n)；
线段树的复杂度为 O(nlog⁡n)O(n\log n)。
总时间复杂度 O(nlog⁡n)O(n\log n)，可以通过此题。

代码细节：

如果直接套用线段树模板（如 P3372），不久应该会发现有点难处理。
具体说明一下线段树的操作：每个位置维护两个数据，一个是在该区间范围内覆盖的长度 cc，第二个是该段被完全覆盖的次数 tagtag。
每次修改时，若完全覆盖，则修改 tagtag，否则修改左右两子区间。
若 tagtag 不为零，cc 的值为该节点维护区间长度；若 tagtag 为零，则 cc 的值为左右两子节点的 cc 值之和（该区间没有被完全覆盖不代表该区间的子区间没有被覆盖）。
这里也验证了我们上文提及的线段树时间复杂度为 O(nlog⁡n)O(n \log n)：cc 仅由 tagtag 决定，不影响复杂度。而修改 tagtag 的单次时间复杂度显然为 O(log⁡n)O(\log n)。
还需要提及的一点就是，由于本题维护的是点，线段树维护区间 [l,r][l,r] 时，实际上维护的是 [l,r+1][l,r+1]。
举个例子，区间 [1,3][1,3] 由 [1,2][1,2] 和 [3,3][3,3] 组成。
这显然不对。[2,3][2,3] 这一段被漏掉了。
而采用我们上面提到的修正方法，区间 [1,3][1,3] 由 [1,2][1,2] 表示，两个子区间在线段树上分别为 [1,1][1,1] 和 [2,2][2,2]，也就是实际上的 [1,2][1,2] 和 [2,3][2,3]。
最后提醒：记得开 long long。
CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node{
	int x,sy,ey,tag;
}line[100005<<1];
map<int,int>mp;
int cnt;
int R[1000005];
int b[200005];
bool cmp(node a,node b){
	if(a.x==b.x)return a.tag>b.tag;
	return a.x<b.x;
}
struct T{
	int c,tag;
}tree[400005<<2];
void pushup(int p,int l,int r){
	if(!tree[p].tag){
		tree[p].c=tree[p<<1].c+tree[p<<1|1].c;
		return;
	}
	tree[p].c=R[r+1]-R[l];
}
void update(int p,int l,int r,int ql,int qr,int k){
	if(l>qr||r<ql)return;
	if(l>=ql&&r<=qr){
		tree[p].tag+=k;
		if(tree[p].tag)tree[p].c=R[r+1]-R[l];
		else pushup(p,l,r);
		return;
	}
	int mid=l+r>>1;
	update(p<<1,l,mid,ql,qr,k);
	update(p<<1|1,mid+1,r,ql,qr,k);
	pushup(p,l,r);
}
signed main(){
	int n;
	cin>>n;
	int p=0;
	for(int i=1;i<=n;i++){
		int x,xx,y,yy;
		cin>>x>>y>>xx>>yy;
//		yy--;
		line[++p].x=x;
		line[p].sy=y;
		line[p].ey=yy;
		line[p].tag=1;
		line[++p].x=xx;
		line[p].sy=y;
		line[p].ey=yy;
		line[p].tag=-1;
	}
	n=p;
	p=0;
	for(int i=1;i<=n;i+=2){
		b[++p]=line[i].sy;
		b[++p]=line[i].ey;
	}
	sort(b+1,b+p+1);
	int mcnt=0;
	for(int i=1;i<=p;i++){
		if(!mp[b[i]]){	
			mp[b[i]]=++cnt;
			R[cnt]=b[i];
		}
	}
	for(int i=1;i<=n;i++){
		line[i].sy=mp[line[i].sy];
		line[i].ey=mp[line[i].ey];
	}
	sort(line+1,line+n+1,cmp);
	int ans=0;
	for(int i=1;i<=n;i++){
		if(i!=1)ans+=tree[1].c*(line[i].x-line[i-1].x);
		update(1,1,cnt,line[i].sy,line[i].ey-1,line[i].tag);
	}
	cout<<ans;
	return 0;
}

评论

共 1 条评论，欢迎与作者交流。

正在加载评论...