[TOC]

字符串部分

一. 字符串通用算法

Ⅰ. 字符串哈希

字符串哈希封装模板（双模数哈希版本）

CPP

struct Hash {
    const int Mod[2] = {(int)1e9 + 7, 998244353};
    const int base[2] = {233, 177};

    vector<int> hsh[2], pw[2];
    void init(string s, int n) {  // index from [1]
        for (int x = 0; x < 2; x++) {
            hsh[x].resize(n + 1);
            pw[x].resize(n + 1);
        }
        pw[0][0] = pw[1][0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int x = 0; x < 2; x++) {
                pw[x][i] = 1ll * pw[x][i - 1] * base[x] % Mod[x];
                hsh[x][i] = (1ll * hsh[x][i - 1] * base[x] + s[i]) % Mod[x];
            }
        }
    }
    pii get_hsh(int l, int r) {
        return {(hsh[0][r] - 1ll * hsh[0][l - 1] * pw[0][r - l + 1] % Mod[0] + Mod[0]) % Mod[0], 
                (hsh[1][r] - 1ll * hsh[1][l - 1] * pw[1][r - l + 1] % Mod[1] + Mod[1]) % Mod[1]}; 
    }
    bool qsame(int l1, int r1, int l2, int r2) {
        return get_hsh(l1, r1) == get_hsh(l2, r2);
    }
} preH, revH;

Ⅰ. kmp 算法

考虑定义 border 集合，设字符串

T

满足：

$T\neq S$ 。
$T$ 是 $S$ 的前缀， $T$ 是 $S$ 的后缀。

则所有满足条件的字符串

T

称为字符串

S

的 border 集合。

对于字符串

S

，定义其

nxt

数组为，

nxt_i

表示

S

的长度为

i

的前缀的 border 集合中最长字符串的长度。

显然暴力构造

nxt

数组时间复杂度为

O(n^2)

。

考虑

nxt

数组的性质：

$nxt_1 = 0$ 。
$nxt_{i+1} \le nxt_i +1$ 。

考虑第二点性质是为什么，因为

nxt_{i+1}

所表示的最长长度的

S[1...i+1]

的 border 中的字符串，在最长情况下只能是：在

nxt_i

所表示的

S[1...i]

的 border 中的最长字符串所在的前缀的后面一个字符，恰好和

S_{i+1}

相同。这才能使得

nxt_{i+1} = nxt_i + 1

。

如果

nxt_{i+1}

能更大的话，考虑去掉最后一个字符得到

nxt_i

，这样就会发现我们现在得到的

nxt_i

比之前求出的大，就矛盾了。

根据这条性质，我们可以暴力跳

nxt

数组，以求出当前位置的

nxt

，正确性证明同上，代码如下：

CPP

void get_nxt(char *s, int n) {
    fail[1] = 0;
    for (int i = 2; i <= n; i++) {
        int pos = fail[i - 1];
        while (pos && s[pos + 1] != s[i]) {
            pos = fail[pos];
        }
        if (s[pos + 1] == s[i]) {
            pos++;
        }
        fail[i] = pos;
    }
}

其中，border 还有一个非常厉害的结论：

对于字符串

S

，如果满足：

\begin{aligned} S \equiv 0 \pmod{|S| - |\operatorname{max\_border}(S)|} \end{aligned}

则

|S| - |\operatorname{max\_border}(S)|

就是

S

的最小循环节长度，否则

S

的最小循环节长度就是

|S|

。

证明的话，就是考虑一段一段对应平移，能证出是循环节，最小的话考虑反证。

exkmp 封装模板

CPP

struct Exkmp {
    int n, m;
    string s, t;    // string (Index from 1)
    vector<int> z, zt;
    /*
    - z  : s 与自己的每个后缀的 lcp 长度
    - zt : s 与 t 的每个后缀的 lcp 长度
    */
    Exkmp(string s): n(SZ(s)), s(" " + s) {    
        z.resize(n + 1, 0);
        zwork();
    }
    Exkmp(string s, string t): n(SZ(s)), m(SZ(t)), s(" " + s), t(" " + t) {
        z.resize(n + 1, 0);
        zt.resize(m + 1, 0);
        zwork();
        ztwork();
    }
    void zwork() {
        z[1] = n;
        int l = 0, r = 0;
        for (int i = 2; i <= n; i++) {
            if (i <= r) {
                z[i] = min(z[i - l + 1], r - i + 1);
            }
            while (i + z[i] <= n && s[z[i] + 1] == s[i + z[i]]) {
                z[i]++;
            }
            if (i + z[i] - 1 > r) {
                l = i; 
                r = i + z[i] - 1;
            }
        }
    }
    void ztwork() { 
        int l = 0, r = 0;
        for (int i = 1; i <= m; i++) {
            if (i <= r) {
                zt[i] = min(z[i - l + 1], r - i + 1);
            }
            while (i + zt[i] <= m && zt[i] + 1 <= n && s[zt[i] + 1] == t[i + zt[i]]) {
                zt[i]++;
            }
            if (i + zt[i] - 1 > r) {
                l = i;
                r = i + zt[i] - 1;
            }
        }
    }
};

可以被 AC 自动机/后缀自动机完全代替，故懒得学了。

Ⅰ. manacher 算法（马拉车算法）

manacher 算法（马拉车算法）封装模板

CPP

namespace Manacher {
    string t;
    vector<int> p;
    void init(string s, int n) {  // index from [1]
        t.resize(2 * n + 1);
        p.resize(2 * n + 1);
        
        t[0] = '#';
        for (int i = 1; i <= n; i++) {
            t[2 * i - 1] = s[i];
            t[2 * i] = '#';
        }
    
        int id = 0, mx = 0; p[0] = 1;
        for (int i = 1; i <= 2 * n; i++) {
            p[i] = (i < mx ? min(p[2 * id - i], mx - i) : 1);
            while (i + p[i] <= 2 * n && i - p[i] >= 0 && t[i + p[i]] == t[i - p[i]]) {
                p[i]++;
            }
            if (i + p[i] > mx) {
                id = i;
                mx = i + p[i];
            }
        }
    }
}

其实也是字符串后缀数据结构的一种，但还是先把他放到回文部分里面了。

建议先理解透彻后缀自动机，再来学回文自动机，这样一些概念和性质会理解得非常快，事半功倍。

Ⅰ. AC 自动机

AC 自动机模板封装

CPP

struct AC_Automat {
    int cnt_id;
    int tr[MAXN][26];
    int fail[MAXN];

    void insert(string s, int n) {	// index from 1
        int u = 0;
        for (int i = 1; i <= n; i++) {
            if (!tr[u][s[i] - 'a']) {
                tr[u][s[i] - 'a'] = ++cnt_id;
            }
            u = tr[u][s[i] - 'a'];
        }
    }
    
    void build() {
        queue<int> q;
        for (int i = 0; i < 26; i++) {
            if (tr[0][i]) {
                q.push(tr[0][i]);
            }
        }
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            for (int i = 0; i < 26; i++) {
                if (tr[u][i]) {
                    fail[tr[u][i]] = tr[fail[u]][i];
                    q.push(tr[u][i]);
                }
                else {
                    tr[u][i] = tr[fail[u]][i];
                }
            }
        }
    }
} ac;

后缀数组封装模板

CPP

namespace SA {
    int n, m;
    char s[MAXN];
    int sa[MAXN], tmp[MAXN], tong[MAXN];
    int rk[MAXN << 1], lst_rk[MAXN << 1];
    int height[MAXN];
    
    void rsort() {
        memset(tong, 0, sizeof(tong));
        for (int i = 1; i <= n; i++) tong[rk[tmp[i]]]++;
        for (int i = 1; i <= m; i++) tong[i] += tong[i - 1];
        for (int i = n; i >= 1; i--) sa[tong[rk[tmp[i]]]--] = tmp[i];
    }
    
    void get_sa() {
        m = 133;
        for (int i = 1;i <= n; i++) rk[i] = s[i];
        for (int i = 1;i <= n; i++) tmp[i] = i;
        rsort();
        
        for (int w = 1; w < n; w <<= 1) {
            int p = 0;
            for (int i = n - w + 1; i <= n; i++) tmp[++p] = i;
            for (int i = 1; i <= n; i++) if(sa[i] > w) tmp[++p] = sa[i] - w;
            rsort();
            
            p = 0;
            memcpy(lst_rk, rk, sizeof(rk));
            for (int i = 1; i <= n; i++) {
                if (lst_rk[sa[i - 1]] == lst_rk[sa[i]] && lst_rk[sa[i - 1] + w] == lst_rk[sa[i] + w]) rk[sa[i]] = p;
                else rk[sa[i]] = ++p;
            }
            m = p;
            
            if (m == n) break; 
        }
    }
    
    void get_height() {
        int len = 0;
        for (int i = 1; i <= n; i++) {
            if (rk[i] == 1) continue;
            if (len) len--;
            int j = sa[rk[i] - 1];
            while (i + len <= n && j + len <= n && s[i + len] == s[j + len]) len++;
            height[rk[i]] = len;
        }
    }
    
    void init(char *t, int len) {
        n = len;
        for (int i = 1; i <= n; i++) {
            s[i] = t[i];
        }
        get_sa();
        get_height();
    }
} using SA::sa;

关于后缀自动机的一些总结。

字符串 $s$ 的 SAM 是接受 $s$ 的所有后缀的最小 DFA。
记 $\operatorname{endpos}(t)$ 为 $t$ 在字符串 $s$ 中所有结束位置的集合，则可以将 $s$ 的所有子串根据 $\operatorname{endpos}$ 划分成若干个等价类。两个不同的 $\operatorname{endpos}$ 集合要么交集为空集，要么一个被另一个包含。
令空串的 $\operatorname{endpos}$ 为 $\{1, 2, \cdots, n\}$ ，则每次向这个串的串首添加 $\Sigma$ 中不同的字符并保存，则相当于把 $\operatorname{endpos}$ 做了分裂，这样一直添加下去会形成一个树形结构（这就是后缀树，可以用线段树合并求出每个 $\operatorname{endpos}$ 集合中的具体元素），每个点相当于一个 $\operatorname{endpos}$ 集合，兄弟结点的集合之间没有交集，父亲结点的集合相当于所有儿子结点的集合的并再并上分裂时丢失的位置（分裂时可能会丢失一些位置是因为，这些位置的前缀已经顶到 $s$ 的头了，没法再串首添加新的字符了）。
由于分裂到最后，每个叶子结点代表的 $\operatorname{endpos}$ 集合中至少有一个位置，且互不相交，所以叶子结点最多有 $n$ 个。如果一个父亲只有一个儿子，那这个结点的集合在分裂时一定丢失了一些位置，否则一个父亲至少有两个儿子，所以树的总结点个数小于等于 $2n - 1$ ，即只有 $O(n)$ 种不同的 $\operatorname{endpos}$ 集合（等价类）。
SAM 的每个结点实际就是一个 $\operatorname{endpos}$ 集合，SAM 中的转移边描述的就是如何在一个 $\operatorname{endpos}$ 集合后添加 $\Sigma$ 中的一个字符转移到另外一个 $\operatorname{endpos}$ 集合。
对于每个结点 $u$ 代表的 $\operatorname{endpos}$ 集合记录一个 $len_u$ 代表这个集合分出的等价类中最长的串的长度，显然最短的长度就是 $len_{fa_u} + 1$ （注意长度一定是连续的，证明比较显然），如果匹配过程中走到某个 $len_u = n$ 的结点的祖先结点上，就说明一个后缀匹配成功了。

CPP

namespace SAM {
    int fa[MAXN << 1], mxlen[MAXN << 1];
    int nxt[MAXN << 1][26];
    
    int cnt_id, lst;
    int epsz[MAXN << 1];
    
    void ins(char ch) {
        int c = ch - 'a';
        int cur = cnt_id++;
        
        epsz[cur] = 1;
        mxlen[cur] = mxlen[lst] + 1;
        
        int p = lst;
        for (; p != -1 && !nxt[p][c]; p = fa[p]) {
            nxt[p][c] = cur;
        }
        
        if(p == -1) {
            fa[cur] = 0;
        }
        else {
            int q = nxt[p][c];
            if (mxlen[p] + 1 == mxlen[q]) {
                fa[cur] = q;
            } else {
                int clone = cnt_id++;
                fa[clone] = fa[q];
                mxlen[clone] = mxlen[p] + 1;
                memcpy(nxt[clone], nxt[q], sizeof(nxt[q]));
                
                fa[cur] = fa[q] = clone;
                for (; p != -1 && nxt[p][c] == q; p = fa[p]) {
                    nxt[p][c] = clone;
                }
            }
        }
        lst = cur;
    }

    vector<int> G[MAXN << 1];
    void dfs(int u) {
        for (auto v : G[u]) {
            dfs(v);
            epsz[u] += epsz[v];
        }
    }
    
    void build(string s, int n) {        // indexed from 1
        cnt_id = 1; lst = 0;
        fa[0] = -1; mxlen[0] = 0;
        for (int i = 1; i <= n; i++) {
            ins(s[i]);
        }
        for (int i = 1; i < cnt_id; i++) {
            G[fa[i]].push_back(i);
        }
        dfs(0);
    }
}

CPP

struct exSAM { 
	int mxlen[(N << 1) + 1], fa[(N << 1) + 1];
	int nxt[(N << 1) + 1][26];
	int cnt_id;

	void init() {
		cnt_id = 1;
		fa[0] = -1;
	}

	int insert(int lst, int c) {
		int cur = nxt[lst][c];
		if (mxlen[cur]) {
			return cur;
		}
		mxlen[cur] = mxlen[lst] + 1;
		
		int p = fa[lst];
		for (; p != -1 && !nxt[p][c]; p = fa[p]) {
			nxt[p][c] = cur;
		}
		if (p == -1) {
			fa[cur] = 0;
			return cur;
		}

		int q = nxt[p][c];
		if (mxlen[p] + 1 == mxlen[q]) {
			fa[cur] = q;
			return cur;
		}

		int clone = cnt_id++;
		fa[clone] = fa[q];
		mxlen[clone] = mxlen[p] + 1;
		for (int i = 0; i < 26; i++) {
			nxt[clone][i] = (mxlen[nxt[q][i]] ? nxt[q][i] : 0);
		}

		fa[cur] = fa[q] = clone;
		for (; p != -1 && nxt[p][c] == q; p = fa[p]) {
			nxt[p][c] = clone;
		}
		return cur;
	}

	void add_str(string s, int n) {		// index from 1
		int u = 0;
		for (int i = 1; i <= n; i++) {
			int c = s[i] - 'a';
			if (!nxt[u][c]) {
				nxt[u][c] = cnt_id++;
			}
			u = nxt[u][c];
		}
	}

	void build() {
		queue<pii> q;
		for (int i = 0; i < 26; i++) {
			if (nxt[0][i]) {
				q.push({0, i});
			}
		}
		while (!q.empty()) {
			auto [lst, c] = q.front();
			q.pop();
			int cur = insert(lst, c);
			for (int i = 0; i < 26; i++) {
				if (nxt[cur][i]) {
					q.push({cur, i});
				}
			}
		}
	}
} sam;

一. 树形数据结构

Ⅰ. 树状数组

树状数组封装模板

CPP

template<typename T>
struct BIT {
    int lim, p;
    vector<T> d;
    void init(int n) {
        d.clear();
        lim = 1, p = 0;
        while (lim < n) {
            lim <<= 1;
            p++;
        }
        d.resize(lim + 1, 0);
    }
    void upd(int x, int v) {
        for (; x <= lim; x += lb(x)) {
            d[x] += v;
        }
    }
    T query(int x) {
        T res = 0;
        for (; x; x -= lb(x)) {
            res += d[x];
        }
        return res;
    }
    T query(int l, int r) {
        return query(r) - query(l - 1);
    }
    T kth(int k) {	// 查找第 k 小
        int pos = lim;
        for (int i = p - 1; i >= 0; i--) {
            if (d[pos - (1 << i)] >= k) {
                pos -= (1 << i);
            } else {
                k -= d[pos - (1 << i)];
            }
        }
        return pos;
    }
};

可持久化线段树封装模板（update 和 query 的具体功能需根据题目重新实现）

CPP

struct Persistable_SegT {
    struct Node {
        int ls, rs;
        ll sum; int tot;
    };
    int cnt_id;
    Node tr[MAXN << 6];

    #define mid ((l + r) >> 1)
    #define ls(x) tr[x].ls
    #define rs(x) tr[x].rs
    #define sum(x) tr[x].sum
    #define tot(x) tr[x].tot

    void push_up(int rt) {
        sum(rt) = sum(ls(rt)) + sum(rs(rt));
        tot(rt) = tot(ls(rt)) + tot(rs(rt));
    }

    void update(int &rt, int pre, int l, int r, int idx, ll v) {
        rt = ++cnt_id;
        ls(rt) = ls(pre);
        rs(rt) = rs(pre);
        if(l == r) {
            tr[rt].sum = tr[pre].sum + v;
            tr[rt].tot = tr[pre].tot + 1;
            return ;
        }
        if (idx <= mid) {
            update(ls(rt), ls(pre), l, mid, idx, v);
        }
        else {
            update(rs(rt), rs(pre), mid + 1, r, idx, v);
        }
        push_up(rt);
    }
    ll query(int lrt, int rrt, int l, int r, int k, ll *lisan) {
        if (k <= 0) {
            return 0;
        }
        if (l == r && tot(rrt) - tot(lrt) > k) {
            return lisan[l] * k;
        }
        if (tot(rrt) - tot(lrt) <= k) {
            return sum(rrt) - sum(lrt);
        }
        ll res = 0;
        int cnt = tot(rs(rrt)) - tot(rs(lrt));
        res += query(rs(lrt), rs(rrt), mid + 1, r, k, lisan);
        res += query(ls(lrt), ls(rrt), l, mid, k - cnt, lisan);
        return res;
    }

    #undef ls
    #undef rs
    #undef sum
    #undef mid

} SegT;

线段树合并封装模板

CPP

struct SegT {
    struct Node {
        int ls, rs, tot;
    } tr[MAXN << 6];
    int cnt_id = 0;

    #define mid ((l + r) >> 1)
    #define ls(x) tr[x].ls
    #define rs(x) tr[x].rs

    void push_up(int rt) {
        tr[rt].tot = tr[ls(rt)].tot + tr[rs(rt)].tot;
    }
    void upd(int &rt, int l, int r, int idx) {
        if (!rt) {
            rt = ++cnt_id;
        }
        if (l == r) {
            tr[rt].tot++;
            return ;
        }
        if (idx <= mid) {
            upd(ls(rt), l, mid, idx);
        } else {
            upd(rs(rt), mid + 1, r, idx);
        }
        push_up(rt);
    }
    int query(int rt, int l, int r, int sp, int ep) {
        if (sp <= l && r <= ep) {
            return tr[rt].tot;
        }
        int res = 0;
        if (sp <= mid) {
            res += query(ls(rt), l, mid, sp, ep);
        }
        if (ep > mid) {
            res += query(rs(rt), mid + 1, r, sp, ep);
        }
        return res;
    }
    int merge(int x, int y) {
        if (!x || !y) {
            return x ^ y;
        }
        tr[x].tot += tr[y].tot;
        ls(x) = merge(ls(x), ls(y));
        rs(x) = merge(rs(x), rs(y));
        return x;
    }

    #undef mid
    #undef ls
    #undef rs
} Tr;

李超线段树封装模板，给定一堆直线，求某个

x

处所有直线的

y

的最大值。

CPP

struct SegT_LiChao {
    static const int MAXN = 1e5 + 10;
    static const int N = 39989 + 10;
    const double eps = 1e-9;
    int fcmp(double x, double y) {
        if (x - y > eps) return 1;
        if (y - x > eps) return -1;
        return 0;
    }
    void chk_mx(pdi &x, pdi y) {
        if (y.fi - x.fi > eps || (fcmp(x.fi, y.fi) == 0 && x.se > y.se)) {
            x = y;
        }
    }

    struct Line {
        double k, b;
        int L, R;
        Line() { k = 0, b = -1; }
        Line(double k, double b, int L, int R): k(k), b(b), L(L), R(R) {}
    };
    int cntl = 0;
    Line p[MAXN];
    void addl(int x1, double y1, int x2, double y2) {
        if (x1 > x2) {
            swap(x1, x2);
            swap(y1, y2);
        }
        if (x1 == x2) {
            p[++cntl] = {0, (double)max(y1, y2), x1, x2};
        }
        else {
            double k = 1.0 * (y2 - y1) / (x2 - x1), b = y1 - k * x1;
            p[++cntl] = {k, b, x1, x2};
        }
        modify(1, 1, N, cntl);
    }
    pdi query(int idx) {
        return query(1, 1, N, idx); 
    }
    double calc(int u, int x) {
        return p[u].k * x + p[u].b;
    }

    #define lson (rt << 1)
    #define rson (rt << 1 | 1)
    #define mid ((l + r) >> 1)

    int tr[N << 2];
    void upd(int rt, int l, int r, int u) {
        int &v = tr[rt];
        int op = fcmp(calc(u, mid), calc(v, mid));
        if (op == 1 || (op == 0 && u < v)) {
            swap(u, v);
        }
        int opl = fcmp(calc(u, l), calc(v, l));
        int opr = fcmp(calc(u, r), calc(v, r));
        if (opl == 1 || (opl == 0 && u < v)) upd(lson, l, mid, u);
        if (opr == 1 || (opr == 0 && u < v)) upd(rson, mid + 1, r, u);
    }
    void modify(int rt, int l, int r, int u) {
        if (p[u].L <= l && r <= p[u].R) {
            upd(rt, l, r, u);
            return ;
        }
        if (p[u].L <= mid) modify(lson, l, mid, u);
        if (p[u].R > mid) modify(rson, mid + 1, r, u);
    }
    pdi query(int rt, int l, int r, int idx) {
        if (l == r) {
            return mkp(calc(tr[rt], idx), tr[rt]);
        }
        pdi res = mkp(calc(tr[rt], idx),  tr[rt]);
        if (idx <= mid) chk_mx(res, query(lson, l, mid, idx));
        else chk_mx(res, query(rson, mid + 1, r, idx));
        return res;
    }

    #undef lson
    #undef rson
    #undef mid
} Tr;

CPP

struct SegT {
    int cnt_id;
    struct Node {
        int ls, rs;
        bool flg;
        int sum;
    } tr[MAXN * 100];

    #define mid ((l + r) >> 1)
    void clear() {
        for (int i = 0; i <= cnt_id; i++) {
            tr[i].ls = tr[i].rs = tr[i].sum = 0;
            tr[i].flg = false;
        }
        cnt_id = 0;
    }
    void push_up(int rt, int l, int r) {
        if (tr[rt].flg) {
            tr[rt].sum = r - l + 1;
        } else {
            tr[rt].sum = tr[tr[rt].ls].sum + tr[tr[rt].rs].sum;
        }
    }
    void upd(int &rt, int l, int r, int sp, int ep) {
        if (!rt) {
            rt = ++cnt_id;
            assert(cnt_id < MAXN * 100);
        }
        if (sp <= l && r <= ep) {
            tr[rt].flg = true;
            push_up(rt, l, r);
            return ;
        }
        if (sp <= mid) {
            upd(tr[rt].ls, l, mid, sp, ep);
        }
        if (ep > mid) {
            upd(tr[rt].rs, mid + 1, r, sp, ep);
        }
        push_up(rt, l, r);
    }
    #undef mid
} Tr;

Fhq_treap 封装模板

CPP

mt19937 mrnd(std::chrono::steady_clock::now().time_since_epoch().count());
int rnd(int l, int r) {
    return mrnd() % (r - l + 1) + l;
}
double rnd01() {
    return mrnd() * 1.0 / UINT32_MAX;
}

namespace Fhq_Treap {
    const int MAXN = 5e5 + 10;

    struct Node {
        int lson, rson;
        int pri, sz;
        ll val;    
    };
    
    int cnt_id;
    Node tree[MAXN << 4];
    queue<int> rub;
    #define ls(x) tree[x].lson
    #define rs(x) tree[x].rson
    
    struct Tree {
        int rt = 0;
        void clear(int x) {
            tree[x] = Node();
            if (x != 0) {
                rub.push(x);
            }
        }
        void all_clear() {
            rt = 0;
            auto vec = iter_id();
            for (auto x : vec) {
                clear(x);
            }
        }
        vector<int> iter_id() {        // 中序遍历
            vector<int> res;
            auto dfs = [&](auto &&self, int x) -> void {
                if (!x) {
                    return ;
                }
                self(self, ls(x));
                res.push_back(x);
                self(self, rs(x));
            };
            dfs(dfs, rt);
            return res;
        }
        vector<ll> iter_val() {
            vector<ll> res;
            auto dfs = [&](auto &&self, int x) -> void {
                if (!x) {
                    return ;
                }
                self(self, ls(x));
                res.push_back(tree[x].val);
                self(self, rs(x));
            };
            dfs(dfs, rt);
            return res;
        }
        int newp(ll val) {
            int cur;
            if (!rub.empty()) {
                cur = rub.front();
                rub.pop();
            } else {
                cur = ++cnt_id;
            }
            tree[cur].val = val;
            tree[cur].pri = rnd(1, 114514);
            tree[cur].sz = 1;
            return cur;
        }
        void push_up(int x) {
            tree[x].sz = tree[ls(x)].sz + tree[rs(x)].sz + 1;
        }
        void split(int x, int &l, int &r, ll val) {
            if (!x) {
                l = r = 0;
                return ;
            }
            if (tree[x].val <= val) {
                l = x;
                split(rs(x), rs(l), r, val);
            } else {
                r = x;
                split(ls(x), l, ls(r), val);
            }
            push_up(x);
        }
        int merge(int x, int y) {
            if (!x || !y) {
                return x ^ y;
            }
            if (tree[x].pri <= tree[y].pri) {
                rs(x) = merge(rs(x), y);
                return push_up(x), x;
            } else {
                ls(y) = merge(x, ls(y));
                return push_up(y), y;
            }
        }
        void insert(ll val) {
            int l_rt, r_rt;
            split(rt, l_rt, r_rt, val);
            rt = merge(merge(l_rt, newp(val)), r_rt);
        }
        void del(ll val) {
            int l_rt, r_rt, mid_rt;
            split(rt, l_rt, r_rt, val);
            split(l_rt, l_rt, mid_rt, val - 1);
            mid_rt = merge(ls(mid_rt), rs(mid_rt));
            rt = merge(merge(l_rt, mid_rt), r_rt);
        }
        int size() {
            return tree[rt].sz;
        }
        int greater_equal_cnt(ll val) {
            int l_rt, r_rt;
            split(rt, l_rt, r_rt, val - 1);
            int res = tree[r_rt].sz;
            rt = merge(l_rt, r_rt);
            return res;
        }
        ll kth_mx(int k) {
            int x = rt;
            while (true) {
                if (tree[rs(x)].sz + 1 < k) {
                    k -= tree[rs(x)].sz + 1;
                    x = ls(x);
                }
                else if (tree[rs(x)].sz + 1 > k) {
                    x = rs(x);
                }
                else {
                    return tree[x].val;
                }
            }
        }
    };
}
using Fhq_Treap::Tree;

CPP

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <ctime>

using namespace std;

const int MAXN=1e5+10;

struct Fhq_treap
{
    #define lson(x) tree[x].ls
    #define rson(x) tree[x].rs

    struct Node
    {
        int ls,rs,sz;
        int pri,val;
        bool rev;
    };

    int root,cnt_id;
    Node tree[MAXN];

    inline int newp(int val)
    {
        tree[++cnt_id].val=val;
        tree[cnt_id].sz=1;
        tree[cnt_id].pri=rand();
        return cnt_id;
    }

    inline void push_up(int x){ tree[x].sz=tree[lson(x)].sz+tree[rson(x)].sz+1; }
    inline void push_down(int x)
    {
        if(tree[x].rev)
        {
            swap(lson(x),rson(x));
            tree[lson(x)].rev^=1;
            tree[rson(x)].rev^=1;
            tree[x].rev=false;
        }
    }

    inline void split(int x,int &l,int &r,int val)
    {
        if(!x) return l=r=0,(void)0;
        
        push_down(x);
        if(tree[lson(x)].sz+1<=val) l=x,split(rson(x),rson(x),r,val-tree[lson(x)].sz-1);
        else r=x,split(lson(x),l,lson(x),val);
        push_up(x);
    }

    inline int merge(int l,int r)
    {
        if(!l || !r) return l^r;

        if(tree[l].pri<tree[r].pri)
        {
            push_down(l);
            rson(l)=merge(rson(l),r);
            return push_up(l),l;
        }
        else
        {
            push_down(r);
            lson(r)=merge(l,lson(r));
            return push_up(r),r;
        }
    }

    inline void insert(int val)
    {
        int l_rt,r_rt;
        split(root,l_rt,r_rt,val-1);
        root=merge(merge(l_rt,newp(val)),r_rt);
    }

    inline void update(int l,int r)
    {
        int l_rt,r_rt,mid_rt;
        split(root,l_rt,r_rt,l-1);
        split(r_rt,mid_rt,r_rt,r-l+1);
        tree[mid_rt].rev^=1;
        root=merge(l_rt,merge(mid_rt,r_rt));
    }

    inline void print(int x)
    {
        if(!x) return ;
        push_down(x);

        print(lson(x));
        printf("%d ",tree[x].val);
        print(rson(x));
    }
};

int n,m;
Fhq_treap Treap;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) Treap.insert(i);

    while(m--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        Treap.update(l,r);
    }
    Treap.print(Treap.root);

    return 0;
}

CPP

struct CartesianTr { 
    int n, rt;
    vector<int> ls, rs;
    vector<int> L, R;
    vector<ll> val;
    void build(int n, const vector<ll>& a) {
        this->n = n;
        ls.resize(n + 1); L.resize(n + 1);
        rs.resize(n + 1); R.resize(n + 1);
        val.resize(n + 1);

        int tp = 0;
        vector st(n + 1, 0);
        for (int i = 1; i <= n; i++) {    // heap 是小根堆
            int p = tp;
            val[i] = a[i];
            while (p && val[st[p]] > val[i]) {
                p--;
            }
            if (p) {
                rs[st[p]] = i;
            }
            if (p < tp) {
                ls[i] = st[p + 1];
            }
            st[++p] = i;
            tp = p;
        }
        rt = st[1];

        auto dfs = [&](auto &&self, int u, int cl, int cr) -> void {
            if (!u) {
                return ;
            }
            L[u] = cl;
            R[u] = cr;
            self(self, ls[u], cl, u - 1);
            self(self, rs[u], u + 1, cr);
        };
        dfs(dfs, rt, 1, n);
    }
};

CPP

__gnu_pbds::tree<std::pair<int, int>, __gnu_pbds::null_type,
                 std::less<std::pair<int, int>>, __gnu_pbds::rb_tree_tag,
                 __gnu_pbds::tree_order_statistics_node_update>
    trr;

insert(x)：向树中插入一个元素 x，返回 std::pair<point_iterator, bool>。
erase(x)：从树中删除一个元素/迭代器 x，返回一个 bool 表明是否删除成功。
order_of_key(x)：返回 x 以 Cmp_Fn 比较的排名（例如使用 std::less<int>，则返回严格小于 x 的元素的个数）。
find_by_order(x)：返回 Cmp_Fn 比较的排名所对应元素的迭代器（注意：排名编号从 $0$ 开始）。
lower_bound(x)：以 Cmp_Fn 比较做 lower_bound，返回迭代器。
upper_bound(x)：以 Cmp_Fn 比较做 upper_bound，返回迭代器。
join(x)：将 x 树并入当前树，前提是两棵树的类型一样，x 树被删除。
split(x,b)：以 Cmp_Fn 比较，小于等于 x 的属于当前树，其余的属于 b 树。
empty()：返回是否为空。
size()：返回大小。

Ⅰ. cdq 分治

利用 cdq 分治离线解决三维偏序问题。

CPP

BIT<int> tr;
tr.init(m);
auto cdq = [&](auto &&self, int l, int r) -> void {
    if (l == r) {
        return ;
    }

    int mid = (l + r) >> 1;
    self(self, l, mid);
    self(self, mid + 1, r);

    int i = l, j = mid + 1, p = 0;
    vector tmp(r - l + 1, Node());
    while (i <= mid && j <= r) {
        if (a[i].y <= a[j].y) {
            tr.upd(a[i].z, a[i].tot);
            tmp[p++] = a[i++];
        } else {
            a[j].ans += tr.query(a[j].z);
            tmp[p++] = a[j++];
        }
    }
    while (i <= mid) {
        tr.upd(a[i].z, a[i].tot);
        tmp[p++] = a[i++];
    }
    while (j <= r) {
        a[j].ans += tr.query(a[j].z);
        tmp[p++] = a[j++];
    }

    for (int k = l; k <= mid; k++) {
        tr.upd(a[k].z, -a[k].tot);
    }
    for (int k = l; k <= r; k++) {
        a[k] = tmp[k - l];
    }
};

在询问答案具有单调性时，二分的思路是，

\text{Solve}(l,r)

表示我二分此问题的答案时，已经知晓了

ans\in [l,r)

，需要做进一步的递归。此时如果有一种手段

\text{check}(x)

表示判断

ans\ge x

是否是合法的，这个问题就得到了解决：令

mid =(l+r)/2

，

\text{check}(mid)

后执行

\text{Solve}(l,mid)

或

\text{Solve}(mid,r)

之一，直到边界情况

(l=r)

。

但面对多个询问，这种方式效率低下。考虑一种方式：

Solve(l,r,Q)

表示同时解决集合

Q

内的所有询问（已知答案的值域在

[l,r]

），利用数据结构对

mid

进行复杂度与

|Q|, [l,r]

有关的处理，而后对集合内所有询问执行

\text{check}(mid)

，将所有询问分为两组

Q_{1}, Q_{2}

分别表示

ans<mid

的与

\ge mid

的，再调用

\text{Solve}(l,mid,Q_{1})

与

\text{Solve}(mid,r,Q_{2})

递归解决下去。

Ⅰ. ST 表（求解区间 RMQ）

CPP

vector rmq(n + 1, vector(21, 0));
for (int i = 1; i <= n; i++) {
    rmq[i][0] = sum[i];
}
for (int j = 1; j <= 20; j++) {
    for (int i = 1; i + (1 << (j - 1)) <= n; i++) {
        rmq[i][j] = max(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
    }
}
vector lg2(n + 1, 0);
for (int i = 2; i <= n; i++) {
    lg2[i] = lg2[i >> 1] + 1;
}
auto qmax = [&](int l, int r) -> int {
    int s = lg2[r - l + 1];
    return max(rmq[l][s], rmq[r - (1 << s) + 1][s]);
};

一. 最短路与最小生成树进阶

Ⅰ. 同余最短路

通过同余构造某些状态，状态之间的关系类似于两点之间的带权有向边。

那么可以以此建图，将某些问题转化为最短路问题，再使用具有优秀时间复杂度的算法求解。

【例题】P3403 跳楼机

[!NOTE]

有 $h$ 个格子，初始在 $1$ 号格子，每次可以

向右移动 $x$ 个格子

向右移动 $y$ 个格子

向右移动 $z$ 个格子

回到第一个格子

问能到达格子的总数量。

首先可以将

h

减去

1

，同时起始楼层设为

0

。

设

d_i

为从

1

开始能够到达的最低的

\bmod x = i

的楼层。

则有

i \stackrel{y}{\longrightarrow} (i+y)\bmod x

和

i \stackrel{z}{\longrightarrow} (i+z)\bmod x

。

像这样建图后，

d_i

就相当于

0 \to i

的最短路，Dijkstra 即可。

最后统计时，对于

d_i \le h

，有贡献

\lfloor\frac{h-d_i}x\rfloor + 1

。

总时间复杂度

\mathcal O(n \log n)

。

CPP

const int N = 1e5 + 7;
const ll inf = (1ull << 63) - 1;
ll h, d[N], ans;
int x, y, z, v[N];
vector< pi > e[N];
pq< pair< ll, int > > q; 

int main() {
    rd(h), --h, rd(x), rd(y), rd(z);
    for (int i = 0; i < x; i++) e[i].pb(mp((i + y) % x, y)), e[i].pb(mp((i + z) % x, z)), d[i] = inf;
    d[0] = 0, q.push(mp(0, 0));
    while (q.size()) {
        int x = q.top().se;
        q.pop();
        if (v[x]) continue;
        v[x] = 1;
        for (ui i = 0; i < e[x].size(); i++) {
            int y = e[x][i].fi, z = e[x][i].se;
            if (d[y] > d[x] + z) d[y] = d[x] + z, q.push(mp(-d[y], y));
        }
    }
    for (int i = 0; i < x; i++)
        if (h >= d[i]) ans += (h - d[i]) / x + 1;
    print(ans);
    return 0;
}

【例题】P2371 [国家集训队]墨墨的等式

上一题的扩展，不再是只能向右走

x,y,z

格，变成能向右走

a_{1}, a_{2}，\cdots, a_{n}

格。

CPP

const int N = 5e5 + 7;
const ll inf = 1e18;
ll l, r, d[N], ans;
int n, x, v[N];
vector< pi > e[N];
pq< pair< ll, int > > q; 

int main() {
    rd(n), rd(l), --l, rd(r), rd(x);
    for (int i = 1; i < x; i++) d[i] = inf;
    for (int i = 1, y; i < n; i++) {
        rd(y);
        for (int i = 0; i < x; i++)
            e[i].pb(mp((i + y) % x, y));
    }
    q.push(mp(0, 0));
    while (q.size()) {
        int x = q.top().se;
        q.pop();
        if (v[x]) continue;
        v[x] = 1;
        for (ui i = 0; i < e[x].size(); i++) {
            int y = e[x][i].fi, z = e[x][i].se;
            if (d[y] > d[x] + z) d[y] = d[x] + z, q.push(mp(-d[y], y));
        }
    }
    for (int i = 0; i < x; i++) {
        if (r >= d[i]) ans += (r - d[i]) / x + 1;
        if (l >= d[i]) ans -= (l - d[i]) / x + 1;
    }
    print(ans);
    return 0;
}

Kruskal 重构树的定义（构造方式）：

一开始，各个结点都在一个以自己为根的连通块中。
执行 Kruskal 算法，重复以下步骤。
1. 把即将加入生成树边集的边，看做一个新点 $x$ ， $x$ 的两儿子分别是 $u$ 所在的连通块对应的根和 $v$ 所在的连通块对应的根， $x$ 的点权是该边的边权。
2. 合并 $u, v$ ，这个合并后的连通块的根是 $x$ 。

性质：

Kruskal 重构树是一个二叉树。
Kruskal 重构树的叶子没有点权，其他点都有点权。
Kruskal 重构树是完全二叉树（除叶结点外，每个结点都有两个儿子）。
原图中的两点 $u, v$ 在 Kruskal 重构树上的 LCA 的点权是原图中 $u$ 到 $v$ 的所有路径中最大边的最小值。

Ⅰ. tarjan 算法求强连通分量并缩点

CPP

int tp = 0, cnt_id = 0, cnt_clr = 0;
vector st(n + 1, 0), inst(n + 1, 0), sz(n + 1, 0);
vector dfn(n + 1, 0), low(n + 1, 0), clr(n + 1, 0);
vector val(n + 1, 0ll);
auto tarjan = [&](auto&& self, int u) -> void {
	st[++tp] = u;
	inst[u] = true;
	dfn[u] = low[u] = ++cnt_id;
	for (auto v : G[u]) {
		if (!dfn[v]) {             // 树边
			self(self, v);
			low[u] = min(low[u], low[v]);
		}
		else if (inst[v]) {        // 返祖边
			low[u] = min(low[u], dfn[v]);
		}
		// 横叉边不需要处理
	}
	
	if (dfn[u] == low[u]) {
		cnt_clr++;
		do {
			sz[cnt_clr]++;
			clr[st[tp]] = cnt_clr;
			val[cnt_clr] += a[st[tp]];
			inst[st[tp]] = false;
		} while (st[tp--] != u);
	}
};

CPP

const int MAXN = 5e5 + 10;

int n, m;
vector<int> G[MAXN];

int dfn[MAXN], low[MAXN];
int st[MAXN], tp, cnt_id;
bool inst[MAXN];
vector<vector<int>> ans;

void tarjan(int u, int fa) {
	
	dfn[u] = low[u] = ++cnt_id;
	st[++tp] = u; inst[u] = true;
	
	int cnt = 0;
	
	for (auto v : G[u]) {
		if (v == fa) {
			cnt++;
			if (cnt == 1) continue;
		}
		if (!dfn[v]) {
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
		}
		else if (inst[v]) {
			low[u] = min(low[u], dfn[v]);
		}
	}
	
	if (dfn[u] == low[u]) {
		vector<int> cur;
		do {
			inst[st[tp]] = false;
			cur.push_back(st[tp]);
		} while (st[tp--] != u);
		ans.push_back(cur);
	}
}

int main() {
	cin >> n >> m; 
	for (int i = 1; i <= m; i++) {
		int u, v;
		cin >> u >> v;
		G[u].push_back(v);
		G[v].push_back(u);
	}
	
	for (int i = 1; i <= n; i++) 
		if (!dfn[i]) {
			tarjan(i, 0);
		}
	
	printf("%d\n", SZ(ans));
	for (auto vec : ans) {
		printf("%d ", SZ(vec));
		for (auto x : vec) {
			printf("%d ", x);
		}
		puts("");
	}
	
	return 0;
}

例题 SDOI2018 战略游戏，建出圆方树后，求两点路径上的圆点数量。

CPP

const int MAXN = 1e5 + 10;

int n, m;
vector<int> G[MAXN], trG[MAXN << 1];
// trG : 存圆方树

int cnt_id, idx_squ;
// cnt_id : 原图的 dfs 序计数器
// idx_squ : 圆方树上方点标号的计数器
int dfn[MAXN << 1], low[MAXN];
int st[MAXN], tp;
void tarjan(int u) {
	dfn[u] = low[u] = ++cnt_id;
	st[++tp] = u;
	for (auto v : G[u]) {
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[u], low[v]);
			
			if (dfn[u] == low[v]) {
				idx_squ++;
				for (int x = 0; x != v; tp--) {
					x = st[tp];
					trG[idx_squ].push_back(x);
					trG[x].push_back(idx_squ);
				}
				trG[idx_squ].push_back(u);
				trG[u].push_back(idx_squ);
			}
		} else {
			low[u] = min(low[u], dfn[v]);
		}
	}
}

// 注意对于圆方树进行处理的数组都需要开两倍空间
int dep[MAXN << 1], dis[MAXN << 1];
int fa[MAXN << 1][20]; 
void dfs_init(int u, int fz, int d) {
	dfn[u] = ++cnt_id;
	fa[u][0] = fz;
	dep[u] = d;
	dis[u] = dis[fz] + (u <= n);
	for (auto v : trG[u]) {
		if (v == fz) {
			continue;
		}
		dfs_init(v, u, d + 1);
	}
}

int qlca(int x, int y) {
	if (dep[x] < dep[y]) {
		swap(x, y);
	}
	int t = dep[x] - dep[y];
	for (int i = 19; i >= 0; i--) {
		if ((t >> i) & 1) {
			x = fa[x][i];
		}
	}
	if (x == y) {
		return x;
	}
	for (int i = 19; i >= 0; i--) {
		if (fa[x][i] != fa[y][i]) {
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}

void init() {
	for (int i = 1; i <= n; i++) {
		G[i].clear();
	}
	for (int i = 1; i <= (n << 1); i++) {
		dfn[i] = 0;
		trG[i].clear();
	}
}

void solve() {
	cin >> n >> m;
	init();
	
	for (int i = 1; i <= m; i++) {
		int u, v;
		cin >> u >> v;
		G[u].push_back(v);
		G[v].push_back(u);	
	}
	
	tp=0; idx_squ = n; 
	cnt_id = 0; tarjan(1);
	cnt_id = 0; dfs_init(1, 0, 0);
	
	for (int j = 1; j <= 19; j++) {
		for (int i = 1; i <= idx_squ; i++) {
			fa[i][j] = fa[fa[i][j - 1]][j - 1];
		}
	}
	
	int q;
	cin >> q;
	while (q--) {
		int s;
		cin >> s;
		vector p(s + 1, 0);
		for (int i = 1; i <= s; i++) {
			cin >> p[i];
		}
		sort(p.begin() + 1, p.begin() + s + 1, [](auto x, auto y) {
			return dfn[x] < dfn[y];
		});
		
		int ans = -2 * s;
		for (int i = 1; i <= s; i++) {
			int x = p[i], y = p[(i == s ? 1 : i + 1)];
			int lca = qlca(x, y);
			ans += dis[x] + dis[y] - 2 * dis[lca];
		}
		
		if (qlca(p[1], p[s]) <= n) {
			ans += 2;
		}
		assert(ans % 2 == 0);
		cout << ans / 2 << '\n';
	}
}

2-SAT 问题，即要求解一组逻辑值

x_{1}, x_{2},\cdots,x_{n}

，使得一个特定的每一项大小都为

2

的最小项逻辑表达式的值为真。

CPP

struct Two_Sat {
    int n, cnt_id, cnt_clr, tp;
    vector<vector<int>> G;
    vector<int> dfn, low, clr, st, inst;
    Two_Sat(int _n) {
        n = _n;
        cnt_id = tp = cnt_clr = 0;
        G.resize(2 * n + 1);
        dfn.resize(2 * n + 1);
        low.resize(2 * n + 1);
        clr.resize(2 * n + 1);
        st.resize(2 * n + 1);
        inst.resize(2 * n + 1);
        for (int i = 1; i <= 2 * n; i++) {
            G[i].clear();
            dfn[i] = low[i] = clr[i] = st[i] = inst[i] = 0;
        }
    }
    void addlim(int x, bool px, int y, bool py) {   // (0/1)x v (0/1)y
        G[x + px * n].push_back(y + (1 - py) * n);
        G[y + py * n].push_back(x + (1 - px) * n);
    }
    void tarjan(int u) {
        dfn[u] = low[u] = ++cnt_id;
        st[++tp] = u; inst[u] = true;
        for (auto v : G[u]) {
            if (!dfn[v]) {
                tarjan(v);
                low[u] = min(low[u], low[v]);
            } else if (inst[v]) {
                low[u] = min(low[u], dfn[v]);
            }
        }
        if (dfn[u] == low[u]) {
            cnt_clr++;
            do {
                inst[st[tp]] = false;
                clr[st[tp]] = cnt_clr;
            } while (st[tp--] != u);
        }
    }
    vector<bool> Tres;
    bool process() {
        for (int i = 1; i <= 2 * n; i++) {
            if (!dfn[i]) {
                tarjan(i);
            }
        }
        for (int i = 1; i <= n; i++) {
            if (clr[i] == clr[i + n]) {
                return false;
            }
        }
        
        Tres.resize(n + 1, false);
        for (int i = 1; i <= n; i++) {
            if (clr[i] < clr[i + n]) {
                Tres[i] = true;
            }
        }
        return true;
    }
};

Ⅰ. 无向图三元环计数

先给无向边定向，度数小的指向度数大的，度数相同编号小的指向编号大的，由于形成偏序关系，所以有向边不会成环。

枚举过程如代码中所示。

复杂度分析考虑根号分治，原图上度数小于等于

\sqrt{m}

的结点最多只有

\sqrt{m}

条出边，原图上度数大于

\sqrt{m}

的结点最多也只有

\sqrt{m}

条出边（不可能有超过

\sqrt{m}

个度数比它还大的）。

所以总时间复杂度等于

O(\sum_{i} out_{i}) = O(m \sqrt{m})

。

CPP

const int MAXN = 1e5 + 10;
const int MAXM = 2e5 + 10;

int n, m;
int from[MAXM], to[MAXM];
vector<int> G[MAXN];
int deg[MAXN];
bool vis[MAXN];

int main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		cin >> from[i] >> to[i];
		deg[from[i]]++; deg[to[i]]++;
	}
	for (int i = 1; i <= m; i++) {
		int u = from[i], v = to[i];
		if (deg[u] > deg[v] || (deg[u] == deg[v] && u > v)) {
            swap(u,v);
        }
		G[u].push_back(v);
	}
	
	int ans = 0;
	for (int u = 1; u <= n; u++) {
		for (int v : G[u]) {
            vis[v] = true;
        }
		
		for (int v : G[u])
			for (int k : G[v])
				if (vis[k]) {
                	ans++;
                }   
		
		for (int v : G[u]) {
            vis[v] = false;
        }
	}
    cout << ans << '\n';
    
	return 0;
}

Ⅰ. Dinic 算法求最大流

dinic 算法一般图的最差时间复杂度为

O(n^2{m})

，单次增广最差时间复杂度为

O(nm)

。但在类二分图上的时间复杂度仅为

O(m\sqrt{n})

。

CPP

namespace Dinic {
    const int MAXN = 2e2 + 10;
    const int MAXM = 2e5 + 10;
    const int INF = (1ll << 31) - 1;
    
    struct Edge { 
        int to, w, nxt; 
    }; 
    
    int n, m, S, T, cnt_e = 1;
    int head[MAXN], curh[MAXN], dep[MAXN];
    Edge e[MAXM];

    void init(int _n) {
        n = _n;
        for (int i = 0; i <= n; i++) {
            head[i] = 0;
        }
        cnt_e = 1;
    }
    
    void addedge(int u, int v, int w, bool flg) {
        e[++cnt_e] = {v, w, head[u]};
        head[u] = cnt_e;
        if (flg) {
            addedge(v, u, 0, false);
        }
    }
    
    bool bfs() {
        for (int i = 1; i <= n; i++) {
            curh[i] = head[i];
            dep[i] = -1;
        }
        
        queue<int> q;
        dep[S] = 0; q.push(S);
        
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            
            for(int i = head[u]; i; i = e[i].nxt) {
                int v = e[i].to, w = e[i].w;
                if(!w || dep[v] != -1) {
                    continue;
                }
                
                dep[v] = dep[u] + 1;
                q.push(v);
                
                if (v == T) {
                    return true;
                }
            }
        }
        return dep[T] != -1;
    }
    
    ll dfs(int u, int flw) {
        if (u == T || !flw) {
            return flw;
        }
        ll res = 0;
        for (int &i = curh[u]; i; i = e[i].nxt) {
            int v = e[i].to, w = e[i].w;
            if(!w || dep[v] != dep[u] + 1) {
                continue;
            }
            int k = dfs(v, min(w, flw));
            
            e[i].w -= k; 
            e[i ^ 1].w += k;
            flw -= k;
            res += k;
            
            if (!flw) {
                break;
            }
        }
        return res;
    }
    
    ll dinic(int s, int t) {
        S = s; T = t;
        ll res = 0;
        while (bfs()) {
            res += dfs(S, INF);
        }
        return res;
    }
} using namespace Dinic;

其实是伪多项式时间的算法，时间复杂度上界为

O(nmf)

，但只要不是刻意对着这个算法卡就跑不满，实际效率还可以。

CPP

namespace MCMF {
    const int MAXN = 5e3 + 10;
    const int MAXM = 2e5 + 10;
    const int INF = (1ll << 31) - 1;
    
    struct Edge { 
        int to, w, c, nxt;
    }; 
    
    int n, m, S, T, cnt_e = 1; ll cost;
    int head[MAXN], curh[MAXN], dis[MAXN];
    bool inq[MAXN];
    Edge e[MAXM];

    void init(int _n) {
        n = _n
        cnt_e = 1;
        cost = 0;
    }
    
    void addedge(int u, int v, int w, int c, bool flg) {
        e[++cnt_e] = {v, w, c, head[u]};
        head[u] = cnt_e;
        if (flg) {
            addedge(v, u, 0, -c, false);
        }
    }
    
    bool spfa() {
        for (int i = 1; i <= n; i++) {
            curh[i] = head[i];
            dis[i] = INF;
        }
        
        queue<int> q;
        dis[S] = 0; q.push(S); inq[S] = true;
        while (!q.empty()) {
            int u = q.front(); q.pop();
            inq[u] = false;

            for (int i = head[u]; i; i = e[i].nxt) {
                int v = e[i].to, w = e[i].w, c = e[i].c;
                if(!w || dis[u] + c >= dis[v]) {
                    continue;
                }
                dis[v] = dis[u] + c;
                if (!inq[v]) {
                    q.push(v);
                    inq[v] = true;
                }
            }
        }
        return dis[T] != INF;
    }
    
    ll dfs(int u, int flw) {
        if (u == T || !flw) {
            return flw;
        }
        
        ll res = 0;
        inq[u] = true;
        for (int &i = curh[u]; i; i = e[i].nxt) {
            int v = e[i].to, w = e[i].w, c = e[i].c;
            if (!w || inq[v] || dis[u] + c != dis[v]) {
                continue;
            }
            int k = dfs(v, min(w, flw));
            
            cost += 1ll * c * k;
            e[i].w -= k;
            e[i ^ 1].w += k;
            flw -= k;
            res += k;
            
            if (!flw) {
                break;
            }
        }
        inq[u] = false;
        return res;
    }
    
    pll mcmf(int s, int t) {
        S = s; T = t;
        ll mxflw = 0;
        while (spfa()) {
            mxflw += dfs(S,INF);
        }
        return {mxflw, cost};
    }
    
} using namespace MCMF;

Ⅰ. 树上启发式合并（Dsu on tree）

每个点到根的路径上不会有超过

O(\log n)

条轻边，这保证了时间复杂度的正确性。

CPP

vector sz(n + 1, 0), dep(n + 1, 0), mxson(n + 1, 0);
auto dfs_init = [&](auto &&self, int u, int fa, int d) -> void {
    sz[u] = 1;
    dep[u] = d;
    int mx = 0;
    for (auto v : G[u]) {
        if (v == fa) {
            continue;
        }
        self(self, v, u, d + 1);
        sz[u] += sz[v];
        if (mx < sz[v]) {
            mx = sz[v];
            mxson[u] = v;
        } 
    }
};
dfs_init(dfs_init, 1, 0, 1);

ll ans = 0;
BIT<int> trcnt; trcnt.init(n);
BIT<ll> trval; trval.init(n);
auto add = [&](auto &&self, int u, int fa, int op) -> void {	// 将子树中每个点的贡献添加到“桶”里面，先不算答案
    trcnt.upd(dep[u], op);
    trval.upd(dep[u], op * dep[u]);

    for (auto v : G[u]) {
        if (v == fa) {
            continue;
        }
        self(self, v, u, op);
    }
};
auto addans = [&](auto &&self, int u, int fa, int d) -> void {	// 计算子树中每个点与“桶”里面已有的贡献的答案
    ll val0 = trval.query(1, dep[u]), cnt0 = trcnt.query(1, dep[u]);
    ll cnt1 = trcnt.query(dep[u] + 1, n);
    ans += 2 * (val0 - cnt0 * d) - cnt0;
    ans += cnt1 * (2 * (dep[u] - d) - 1);
    for (auto v : G[u]) {
        if (v == fa) {
            continue;
        }
        self(self, v, u, d);
    }
};

auto dfs_calc = [&](auto &&self, int u, int fa, bool ismxson) -> void {
    for (auto v : G[u]) {
        if(v == fa || v == mxson[u]) {
            continue;
        }
        self(self, v, u, false);
    }
    if (mxson[u]) {
        self(self, mxson[u], u, true);
    }
    for (auto v : G[u]) {
        if (v == fa || v == mxson[u]) {
            continue;
        }
        addans(addans, v, u, dep[u]);
        add(add, v, u, 1);
    }

    trcnt.upd(dep[u], 1);
    trval.upd(dep[u], dep[u]);
    if (!ismxson) {
        add(add, u, fa, -1);
    }
};
dfs_calc(dfs_calc, 1, 0, false);

没啥好说的，直接上代码。

CPP

vector<int> G[MAXN];
int val1[MAXN], val2[MAXN];
int mxson[MAXN], fa[MAXN], dep[MAXN], sz[MAXN];
void dfs_init(int u, int fz, int d) {
	int Mx = 0;
	sz[u] = 1; dep[u] = d; fa[u] = fz;
	for (auto v : G[u]) {
		if (v == fz) {
			continue;
		}
		dfs_init(v, u, d + 1);
		sz[u] += sz[v];
		if (sz[v] > Mx) {
			Mx = sz[v];
			mxson[u] = v;
		}
	}
}
int cnt_id;
int tp[MAXN], idx[MAXN];
void dfs_tp(int u, int tpfa) {
	tp[u] = tpfa;
	idx[u] = ++cnt_id;
	val2[idx[u]] = val1[u];
	
	if (mxson[u]) {
		dfs_tp(mxson[u], tpfa);
	}
	for (auto v : G[u]) {
		if (idx[v]) {
			continue;
		}
		dfs_tp(v, v);
	}
}

void Tree_add(int x, int y, int v) {	
	while (tp[x] != tp[y]) {
		if (dep[tp[x]] < dep[tp[y]]) {
			swap(x,y);
		}
		tr.upd(1, 1, n, idx[tp[x]], idx[x], v);
		x = fa[tp[x]];
	}
	if (dep[x] > dep[y]) {
		swap(x, y);
	}
	tr.upd(1, 1, n, idx[x], idx[y], v);
}

int Tree_query(int x, int y) {
	ll res = 0;
	while (tp[x] != tp[y]) {
		if (dep[tp[x]] < dep[tp[y]]) {
			swap(x,y);
		}
		res = (res + tr.query(1, 1, n, idx[tp[x]], idx[x])) % Mod;
		x = fa[tp[x]];
	}
	if (dep[x] > dep[y]) {
		swap(x,y);
	}
	res = (res + tr.query(1, 1, n, idx[x], idx[y])) % Mod;
	return res;
}

超强防卡版。

CPP

const ull mask = mt19937_64(time(0))();
auto shift = [&](ull x) -> ull {
	x ^= mask;
	x ^= x << 13;
	x ^= x >> 7;
	x ^= x << 17;
	x ^= mask;
	return x;
};
vector sub(n + 1, 0llu), rt(n + 1, 0llu);
auto dfs_sub = [&](auto&& self, int u, int fa) -> void {
	sub[u] = 1;
	for (auto v : G[u]) {
		if (v == fa) {
			continue; 
		}
		self(self, v, u);
		sub[u] += shift(sub[v]);
	}
};
auto dfs_rt = [&](auto&& self, int u, int fa) -> void {
	for (auto v : G[u]) {
		if (v == fa) {
			continue; 
		}
		rt[v] = sub[v] + shift(rt[u] - shift(sub[v])); 
		self(self, v, u);
	}
};
auto dfs_hsh = [&](auto&& self, int u, int fa) -> ull {
	ull res = shift(rt[u]);
	for (auto v : G[u]) {
		if (v == fa) {
			continue; 
		}
		res += shift(self(self, v, u));
	}
	return res;
};

关于点分树的一些性质，通过一个例题来讲解。

LuoguP6329 【模板】点分树 | 震波

给一棵 $n$ 的点的树，有点权，有 $q$ 次操作。每次修改一个点 $x$ 的点权或查询到给定点 $x$ 距离 $\le k$ 的所有点的点权和。

代码前期部分主要是要找重心，然后分治，建立点分树，后面就是普通的暴力跳点分树上的

fa

然后在权值线段树上进行修改。

直接放一个别人的代码。

CPP

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
	x=0;char c=getchar();T neg=1;
	while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	x*=neg;
}
const int MAXN=1e5;
const int MAXP=5e6;
const int LOG_N=17;
const int INF=1e9;
int n,qu,a[MAXN+5];
int hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int fa[MAXN+5][LOG_N+2],dep[MAXN+5];
void dfs0(int x,int f){		// 预处理 dep 等信息
	fa[x][0]=f;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(y==f) continue;
		dep[y]=dep[x]+1;dfs0(y,x);
	}
}
int getlca(int x,int y){	// 求原树上的 lca, 用来算距离
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=LOG_N;~i;i--) if(dep[x]-(1<<i)>=dep[y]) x=fa[x][i];
	if(x==y) return x;
	for(int i=LOG_N;~i;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
int getdis(int x,int y){return dep[x]+dep[y]-(dep[getlca(x,y)]<<1);}
int siz[MAXN+5],mx[MAXN+5],cent=0;
bool vis[MAXN+5];
void findcent(int x,int f,int tot){		// 找重心
	siz[x]=1;mx[x]=0;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(y==f||vis[y]) continue;
		findcent(y,x,tot);chkmax(mx[x],siz[y]);siz[x]+=siz[y];
	} chkmax(mx[x],tot-siz[x]);
	if(mx[x]<mx[cent]) cent=x;
}
int dfa[MAXN+5];
void divcent(int x,int tot){	// 点分治，建立点分树
//	printf("%d\n",x);
	vis[x]=1;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(vis[y]) continue;
		cent=0;int sz=(siz[y]<siz[x])?siz[x]:(tot-siz[x]);
		findcent(y,x,sz);dfa[cent]=x;divcent(cent,sz);
	}
}
struct segtree{	// 权值线段树
	int rt[MAXN+5],ncnt=0;
	struct node{int ch[2],val;} s[MAXP+5];
	void modify(int &k,int l,int r,int p,int x){
		if(!k) k=++ncnt;
		if(l==r){s[k].val+=x;return;}
		int mid=(l+r)>>1;
		if(p<=mid) modify(s[k].ch[0],l,mid,p,x);
		else modify(s[k].ch[1],mid+1,r,p,x);
		s[k].val=s[s[k].ch[0]].val+s[s[k].ch[1]].val;
	}
	int query(int k,int l,int r,int ql,int qr){
		if(!k) return 0;
		if(ql<=l&&r<=qr) return s[k].val;
		int mid=(l+r)>>1;
		if(qr<=mid) return query(s[k].ch[0],l,mid,ql,qr);
		else if(ql>mid) return query(s[k].ch[1],mid+1,r,ql,qr);
		else return query(s[k].ch[0],l,mid,ql,mid)+query(s[k].ch[1],mid+1,r,mid+1,qr);
	}
} w1,w2;
void modify(int x,int v){
	int cur=x;
	while(cur){
		w1.modify(w1.rt[cur],0,n-1,getdis(cur,x),v);
		if(dfa[cur]) w2.modify(w2.rt[cur],0,n-1,getdis(dfa[cur],x),v);
		cur=dfa[cur];
	}
}
int query(int x,int k){
	int cur=x,pre=0,ret=0;
	while(cur){
		if(getdis(cur,x)>k){
			pre=cur;cur=dfa[cur];continue;
		}
		ret+=w1.query(w1.rt[cur],0,n-1,0,k-getdis(cur,x));
		if(pre) ret-=w2.query(w2.rt[pre],0,n-1,0,k-getdis(cur,x));
		pre=cur;cur=dfa[cur];
	} return ret;
}
int main(){
	scanf("%d%d",&n,&qu);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);adde(u,v);adde(v,u);}
	dfs0(1,0);for(int i=1;i<=LOG_N;i++) for(int j=1;j<=n;j++)
		fa[j][i]=fa[fa[j][i-1]][i-1];
	mx[0]=INF;cent=0;findcent(1,0,n);divcent(cent,n);
//	for(int i=1;i<=n;i++) printf("%d\n",dfa[i]);
	for(int i=1;i<=n;i++) modify(i,a[i]);
	int preans=0;
	while(qu--){
		int opt,x,y;scanf("%d%d%d",&opt,&x,&y);
		x^=preans;y^=preans;
		if(opt==0){preans=query(x,y);printf("%d\n",preans);}
		else{modify(x,y-a[x]);a[x]=y;}
	}
	return 0;
}

Ⅰ. 欧拉路的判定与求解

欧拉路存在的充要条件：

图是连通的，若不连通不可能一次性遍历所有边。
对于无向图：有且仅有两个点，与其相连的边数为奇数，其他点相连边数皆为偶数；或所有点皆为偶数边点。

对于两个奇数点，一个为起点，一个为终点。起点需要出去，终点需要进入，故其必然与奇数个边相连。

如果存在这样一个欧拉路，其所有的点相连边数都为偶数，那说明它是欧拉回路。

因为此时它的起点即是终点，出去后还会回来，刚好形成偶数边。
对于有向图：除去起点和终点，所有点的出度与入度相等。起点出度比入度大 $1$ ，终点入度比出度大 $1$ 。若起点终点出入度也相同，则为欧拉回路。

Hierholzer 算法求欧拉回路。

CPP

vector<int> ans;
void Hierholzer(int u) {
    while (!G[u].empty()) {
        auto v = *G[u].begin();
        G[u].erase(G[u].begin());
        G[v].erase(G[v].find(u));
        Hierholzer(v);
    }
    ans.push_back(u);
}

Ⅱ. 平面图的判定

平面图判定定理：

如果一个图 $G$ 不存在任意一个子图为五阶完全图或者左右两部都为大小都为 $3$ 的完全二分图，那么图 $G$ 就是平面图。

给定若干个结点构成的集合

P

，要求从原图

G = (V, E)

中找出一个包含

P

中所有点的连通子图，且边权和最小。

考虑使用状压 dp，设

f_{i, S}

代表以

i

为根，包含集合

S

中所有点的最小代价。

一棵以

i

为根的树有两种情况，第一种是

i

的度数为

1

，可以考虑枚举树上与

i

相邻的点

j

，则

f_{i,S} \leftarrow f_{j,S} + w_{i, j}

对于度数大于

1

的情况，可以划分成若干个子树，则

f_{i, S} \leftarrow f_{i, T} + f_{i, S - T}

对于第一种转移，发现松弛过程与最短路一致，可以跑一个全源的 dij。对于第二种转移枚举子集即可。

总时间复杂度

O(n\times 3^{|P|} + m\log m \times 2^{|P|})

。

CPP

memset(f, 0x3f, sizeof(f));
for (int i = 1; i <= k; i++) {
    cin >> p[i];
    f[1 << (i - 1)][p[i]] = 0;
}

for (int s = 1; s < (1 << k); s++) {
    for (int i = 1; i <= n; i++) {
        for (int t = (s - 1) & s; t; t = (t - 1) & s) {
            chk_min(f[s][i], f[t][i] + f[s ^ t][i]);
        }
        pq.push({-f[s][i], i});
    }
    dij(s);		
}

int ans = 1e9;
for (int i = 1; i <= n; i++) { 
    chk_min(ans, f[(1 << k) - 1][i]);
}
cout << ans << '\n';

数学部分

一. 数论基础

Ⅰ. 扩展欧几里得算法（exgcd）

求方程组

ax + by = \gcd(a, b)

的一组解

(x_{0}, y_{0})

。

CPP

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }
    int g = exgcd(b, a % b, x, y);
    int tmp = x; x = y;
    y = tmp - a / b * y;
    return g;
}

扩展中国剩余定理推导如下，解决

n

组同余方程的方程组：

\left\{ \begin{aligned} x &\equiv r_1 \pmod {m_1} \\ x &\equiv r_2 \pmod {m_2} \\ & ... \\ x &\equiv r_n \pmod {m_n} \\ \end{aligned} \right.

这里的

m_i

并不一定保证两两互质，是没有任何限制的。

扩展中国剩余定理的本质思想其实就是把两个同余方程合并成为一个同余方程，考虑：

\left\{ \begin{aligned} a \equiv r_1 \pmod{m_1} \\ a \equiv r_2 \pmod{m_2} \\ \end{aligned} \right.

假设这两个方程存在一个等价的方程

a \equiv r \pmod m

。

那么设

a = k_1 m_1 + r_1 = k_2 m_2 + r_2

，我们得到：

k_1 m_1 - k_2 m_2 = r_2 - r_1

。

现在我们要求一组解

(k_1^{'} , k_2^{'})

。

根据裴蜀定理，当

\gcd(m_1,m_2) \nmid (r_2-r_1)

时，该方程无整数解。

这样，在判断有解后，很容易通过扩展欧几里得算法求出一组解

(k_1^{'},k_2^{'})

。

这样，我们就求出了一个解

a_0 = k_1^{'} m_1 + r_1

。

我们又发现，

a_0 + \operatorname{lcm}(m_1,m_2)

也是一组合法解。

所以

a \equiv a_0 \pmod{\operatorname{lcm}(m_1,m_2)}

，但是我们需要证明这涵盖了所有合法解。

假设在模

\operatorname{lcm}(m_1,m_2)

的剩余系中存在

x,y

使得：

\left\{ \begin{aligned} x \equiv r_1 \pmod{m_1} \\ x \equiv r_2 \pmod{m_2} \\ \end{aligned} \right. \left\{ \begin{aligned} y \equiv r_1 \pmod{m_1} \\ y \equiv r_2 \pmod{m_2} \\ \end{aligned} \right.

并且

x\neq y

。那么，一定满足：

\left\{ \begin{aligned} x-y \equiv 0 \pmod{m_1} \\ x-y \equiv 0 \pmod{m_2} \\ \end{aligned} \right.

所以

\operatorname{lcm}(m_1,m_2) \mid (x-y)

，又因为

x,y

均为模

\operatorname{lcm}(m_1,m_2)

的剩余系中的元素，所以只能存在

x=y

一种情况。

所以在模

\operatorname{lcm}(m_1,m_2)

的剩余系种只能存在一个解。

所以

a\equiv a_0 \pmod {\operatorname{lcm}(m_1,m_2)}

是原同余方程组的通解。

至此，我们

O(\log n)

实现了两个同余方程的合并，然后我们依次合并

n

个同余方程，就是扩展中国剩余定理。

CPP

const int MAXN = 1e5 + 10;

ll mul(ll x, ll y, ll p) {
	int flg = 1;
	if (y < 0) y = -y, flg = -1;
	ll res = 0;
	while (y) {
		if (y & 1) res = (res + x) % p;
		x = (x + x) % p;
		y >>= 1;
	}
	return res * flg;
}

ll gcd(ll a, ll b) {
	return !b ? a : gcd(b, a % b);
}

ll lcm(ll a, ll b) {
	return a / gcd(a,b) * b;
}

ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b)	return x = 1, y = 0, a;
	ll g = exgcd(b, a % b, x, y);
	ll tmp = x;
	x = y, y = tmp - a / b * y;
	return g;
}

int n;
ll a[MAXN], b[MAXN];

void excrt()
{
	ll r1 = b[1], m1 = a[1];
	for(int i = 2; i <= n; i++)
	{
		ll r2 = b[i], m2 = a[i];
		
		ll k1, k2;
		ll g = exgcd(m1, -m2, k1, k2);
		
		m1 = lcm(m1, m2);
		
        k1 = mul(k1, ((r2 - r1) / g), m1);
        k2 = mul(k2, ((r2 - r1) / g), m1);
        
		r1 = ((mul(k2, m2, m1) + r2) % m1 + m1) % m1;
	}
	printf("%lld\n", r1);
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	
		scanf("%lld%lld", &a[i], &b[i]);
	excrt();
	return 0;
}

考虑使用群论的基本知识证明欧拉定理：若

a \perp n

，则有

\begin{aligned} a^{\varphi(n)} \equiv 1 \pmod{n} \end{aligned}

设

n

是一个正整数，令

(G, \cdot)

为整数集合

\mathbb{Z}

模

n

且与

n

互质的剩余类关于乘法构成的群，显然

|G| = \varphi(n)

。

先简要证明一下

(G, \cdot)

满足群的定义：

封闭性

若 $a,b$ 均与 $n$ 互质，根据唯一分解定理，有 $a\cdot b$ 与 $n$ 互质，运算满足封闭性。
结合律

若 $a, b, c$ 均与 $n$ 互质，根据同余的理论，有 $(a \cdot b) \cdot c \equiv a \cdot (b \cdot c) \pmod n$ ，运算满足结合律。
存在幺元

显然 $1$ 与 $n$ 互质，所以 $1 \in G$ ，且满足 $1 \cdot a \equiv a \cdot 1 \equiv a \pmod{n}$ ，故 $1$ 为群 $G$ 的幺元；
存在逆元

若 $a$ 与 $n$ 互质，根据裴蜀定理可以推导出，存在正整数 $b \perp n$ 使得 $ab \equiv 1 \pmod{n}$ ，所以 $G$ 中的所有元素均存在逆元。

由拉格朗日定理的推论

有限群 $G$ 的任一元素 $a$ 的阶 $o(a)$ 整除 $G$ 的阶；于是 $a^{|G|} = e$ 。

我们立即得到

\begin{aligned} a^{|G|} \equiv 1 \pmod{n} \end{aligned}

代入

|G| = \varphi(n)

即可得到欧拉定理。

扩展欧拉定理描述如下（不再进行证明），这里只要求

a, m

为整数，不需要

a, m

互质。

a^{b} \equiv \left\{ \begin{aligned} &a^{b} &,b\le \varphi(m)\\ &a^{b \bmod \varphi(m) + \varphi(m)}&,b > \varphi(m) \end{aligned} \right. \pmod{m}

定义

1. 阶：

对于

a\in \mathbb{Z} , m\in \mathbb{N^*} , \gcd(a,m)=1

。

满足同余式

a^n \equiv 1 \pmod m

的最小正整数

n

称作

a

模

m

的阶，记作

\delta_m(a)

。

2. 原根：

对于

a\in \mathbb{Z} , m\in \mathbb{N^*} , \gcd(a,m)=1

。

由欧拉定理，我们知道

a^{\varphi(m)} \equiv 1 \pmod m

。若

\delta_m(a) = \varphi(m)

，则称

a

为模

m

的原根。

性质

1. 阶：

「阶」性质 $1$ ：

a , a^2 , a^3 , ...,a^{\delta_m(a)}

模

m

两两不同余。

「阶」性质 $2$ ： 若

a^n \equiv 1 \pmod m

，则

\delta_m(a)\mid n

。

推论：

a^p \equiv a^q \pmod m

，则

p \equiv q \pmod{ \delta_m(a)}

。

「阶」性质 $3$ ： 若

a,b\in \mathbb{Z} , m\in \mathbb{N^*} , \gcd(a,m) = \gcd(b,m) = 1

，则

\delta_m(ab) = \delta_m(a)\delta_m(b) \Longleftrightarrow \gcd(\delta_m(a),\delta_m(b))=1

。

「阶」性质 $4$ ： 若

a\in \mathbb{Z} , k \in \mathbb{N} , m\in \mathbb{N^*} , \gcd(a,m)=1

，则

\delta_m(a^k) = \frac{\delta_m(a)}{\gcd(\delta_m(a),k)}

。

2. 原根：

「原根」性质 $1$ ：（原根个数） 若一个数

m

有原根，则其原根个数为

\varphi(\varphi(m))

。

「原根」性质 $2$ ：（原根存在定理） 一个数

m

存在原根当且仅当

m\in \{ 2,4,p^{\alpha},2p^{\alpha} \mid p\text{ is an odd prime} , \alpha \in \mathbb{N^*}\}

。

「原根」性质 $3$ ：（最小原根） 若一个数

m

有原根，则其最小原根一定是不多于

m^{0.25}

级别的。（这个性质是由我国数学家王元在

\text{1959}

年证明的）

证明

这里简单证明一下**「原根」性质

1

**，因为在证明过程中的结论需要用于快速求一个数的所有原根。至于其他的证明，有空再回来补一补吧。

**证明：「原根」性质

1

设

m

存在一个原根

g

。

首先，根据**「阶」性质

1

** 可得：

g,g^2, ... , g^{\varphi(m)}

两两不同，且都与

m

互质。因为能成为

m

原根的数至少与

m

互质，这样

g

的次幂就覆盖了所有可能成为原根的数，所以

g^x , x\in [1,\varphi(m)]

一定能表示出

m

的所有原根。

接着，根据**「阶」性质

4

** 可得：

\delta_m(g^k) = \frac{\delta_m(g)}{\gcd(\delta_{m}(g),k)} = \frac{\varphi(m)}{\gcd(\varphi(m),k)}

如果

\gcd(\varphi(m),k)=1

，则

\delta_m(g^k) = \varphi(m)

，

g^k

也是

m

的原根。

容易发现，满足

1\le k < \varphi(m)

且

\gcd(\varphi(m),k)=1

的

k

有

\varphi(\varphi(m))

个。

\text{Q.E.D.}

求原根的算法流程：

下面是求一个数

m

的原根的算法流程：

预处理：
1. 线性筛出 $m$ 以内所有素数和所有数的欧拉函数。
2. 对于每一个 $m$ 以内的素数，求出所有不大于 $m$ 的奇素数 $p^{\alpha}$ 和 $2p^{\alpha}$ 。
3. 判断 $m$ 是否有原根。
求最小原根 $a$ $a$ ：
1. 求出 $\varphi(m)$ 的所有因数。
2. 从小到大枚举与 $m$ 互质的数 $a$ 。
3. 对于 $\varphi(m)$ 的每个因数 $x$ ，若 $a^x \equiv 1 \pmod m$ 且 $j\neq \varphi(m)$ ，则 $a$ 不是 $m$ 的原根。
求所有原根：
1. 枚举 $\varphi(m)$ 以内的所有数 $i$ 。
2. 若 $\gcd(\varphi(m),i)=1$ ，则 $a^i$ 为一个新的原根。

CPP

// 代码有些古老，但是这里重在理论，所以代码就没改

const int MAXM=1e6+10;

inline int gcd(int x,int y){ return !y ? x : gcd(y,x%y); }
inline ll ksm(ll x,ll y,ll p)
{
	ll res=1;
	while(y)
	{
		if(y&1) res=res*x %p;
		x=x*x %p;
		y>>=1;
	}
	return res;
}

int pcnt;
bool isnp[MAXM];
int p[MAXM];
int phi[MAXM];

inline void init(int n)
{
	isnp[0]=isnp[1]=true;
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!isnp[i])
		{
			p[++pcnt]=i;
			phi[i]=i-1;
			for(int cur=i;(ll)cur*i<=n;cur*=i)
				phi[cur*i]=i*phi[cur];
		}
		for(int j=1;j<=pcnt && (ll)i*p[j]<=n;j++)
		{
			isnp[i*p[j]]=true;
			int x=i,y=p[j];
			while(x%p[j]==0) x/=p[j],y*=p[j];
			phi[x*y]=phi[x]*phi[y];
			if(i%p[j]==0) break;
		}
	}
}

inline void solve()
{
	int m,d;
	scanf("%d%d",&m,&d);
	bool fg=false;
	for(int i=1;i<=pcnt && p[i]<=m;i++)
	{
		if(p[i]%2==0) continue;
		ll cur=p[i];
		for(;cur<=m;cur*=p[i])
			if(cur==m || 2*cur==m)
			{
				fg=true;
				break;
			}
	}
	if(m!=2 && m!=4 && !fg)
	{
		puts("0\n");
		return ;
	}
	
	vector<int> yueshu;
	for(int i=1;i*i<=phi[m];i++)
	{
		if(phi[m]%i) continue;
		yueshu.push_back(i);
		if(i*i!=phi[m]) yueshu.push_back(phi[m]/i);
	}
	sort(yueshu.begin(),yueshu.end());
	
	int a=-1;
	for(int i=1;i<=m;i++)
	{
		if(gcd(i,m)>1) continue;
		fg=true;
		for(int j=0;j<(int)yueshu.size();j++)
			if(ksm(i,yueshu[j],m)==1 && yueshu[j]!=phi[m])
			{
				fg=false;
				break;
			}
		if(fg)
		{
			a=i;
			break;
		}
	}
	
	vector<int> pr;
	for(int i=1;i<=phi[m];i++)
	{
		if(gcd(i,phi[m])>1) continue;
		pr.push_back(ksm(a,i,m));
	}
	sort(pr.begin(),pr.end());
	
	printf("%d\n",(int)pr.size());
	for(int i=0;i<(int)pr.size();i++)
		if((i+1)%d==0)
			printf("%d ",pr[i]),fg=true;
	puts("");
}

int main()
{
	init(MAXM-10);
	int T;
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}

BSGS 与 exBSGS

大步小步算法，利用了根号分治的思想，求解

a^{x} \equiv b \pmod{p}

的最小整数解。

CPP

namespace BSGS {
    const int INF = (1ll << 31) - 1;
    int bsgs(int a, int p, int b, int coef) {     // gcd(a, p) = 1, 找到 a ^ x \equiv b (mod p) 的最小整数解
        a %= p;
        b %= p;

        int t = ceil(sqrt(p));
        unordered_map<int, int> mp;
        int cur = b;
        for (int i = 0; i <= t; i++) {
            mp[cur] = max(mp[cur], i + 1);
            cur = 1ll * cur * a % p;
        }
    
        int mul = 1;
        for (int i = 1; i <= t; i++) {
            mul = 1ll * mul * a % p;
        }
        cur = mul;
        int res = INF;
        for (int i = 1; i <= t; i++) {
            int v = 1ll * coef * cur % p;
            if (mp[v]) {
                res = min(res, i * t - (mp[v] - 1));
            }
            cur = 1ll * cur * mul % p;
        }

        if (res == INF) {
            return -1;
        }
        return res;
    }
    int exbsgs(int a, int p, int b){   // gcd(a, p) != 1 时
        a %= p;
        b %= p;
        if (b == 1 || p == 1) {
            return 0;
        }
        int k = 0, coef = 1;
        while (true) {
            int g = __gcd(a, p);
            if (g == 1) {
                break;
            }
            if (b % g != 0) {
                return -1;
            }
            k++; b /= g; p /= g;
            coef = (1ll * coef * a / g) % p;
            if (coef == b) {
                return k;
            }
        }
        int res = bsgs(a, p, b, coef);
        if (res == -1) {
            return -1;
        } else {
            return res + k;
        }
    } 
}

Ⅰ. 线性筛

线性筛（筛

\mu

函数）模板

CPP

const int N = 5e7;
const int MAXN = N + 10;

bool isnp[MAXN];
int pcnt, p[MAXN], mu[MAXN];
void init_eular(int n) {
    isnp[1] = true; mu[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!isnp[i]) {
            p[++pcnt] = i;
            mu[i] = -1;
        }
        for (int j = 1; j <= pcnt && i * p[j] <= n; j++) {
            int x = i, y = p[j];
            while (x % p[j] == 0) {
                x /= p[j];
                y *= p[j];
            }
            if (x > 1) {
                mu[x * y] = mu[x] * mu[y];
            }
            isnp[x * y] = true;
            if (i % p[j] == 0) {
                break;
            }
        }
    }
}

反演过程

设

\mathbf{g} = \mathbf{f} * 1

，那么

\mathbf{f} = \mathbf{f} * 1 * \mu = \mathbf{g} * \mu

。(其实这就是莫比乌斯反演的公式)

同理，设

\mathbf{g} = \mathbf{f} * \mathbf{id^k}

，设

\mathbf{t}(n) = \mu(n)\cdot n^k

，易证

\mathbf{id^k} * \mathbf{t} = \epsilon

，所以

\mathbf{f} = \mathbf{f} * \mathbf{id^k} * \mathbf{t} = \mathbf{g} * \mathbf{t}

。

常用数论函数

常用结论

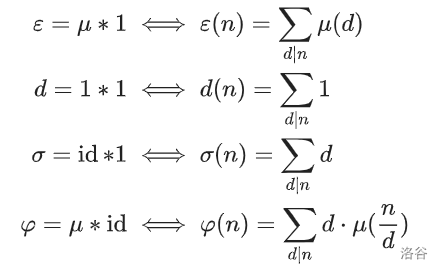
证明一下最后一个：

\begin{aligned} \varphi(n) & = \sum\limits_{i=1}^{n} [\gcd(i,n)=1] \\ & = \sum\limits_{i=1}^{n} \sum\limits_{d|\gcd{(i,n)}} \mu(d) \\ & = \sum\limits_{d|n} \mu(d) \sum\limits_{d|i,i\le n} 1 \\ & = \sum\limits_{d|n} \mu(d) \frac{n}{d} \\ \end{aligned}

下面是做题中遇到的一些重要结论：
1. 与 $n$ 互质的数的和等于 $\frac{\varphi(n)*n}{2}$ ， $n=1$ 时除外。
  
  略证：考虑与 $n$ 互质的数一定成对出现，即若 $x\perp n$ ，则 $(n-x)\perp n$ ，然后显然可证。
2. $\mathbf{d}(nm) = \sum\limits_{x|n}\sum\limits_{y|m} [\gcd(x,y)=1]$ 。
  
  略证：懒得写了，点这儿。
3. $\sum\limits_{i=1}^{n} \lfloor \frac{n}{i} \rfloor = \sum\limits_{i=1}^{n} \mathbf{d}(n)$ 。
4. $\sum\limits_{i=1}^{n} \mu^2(n) = \sum\limits_{d=1}^{\sqrt{n}} \mu(d) \lfloor \frac{n}{d^2}\rfloor$ 。

解决问题

给定数论函数

\mathbf{f}

，在低于线性的时间复杂度下求出

\mathbf{S}(n) = \sum\limits_{i=1}^{n} \mathbf{f}(i)

。

解决方法

假设我们有数论函数

\mathbf{g}

，能快速对

\mathbf{f} * \mathbf{g}

求前缀和，即能够快速求出

\sum\limits_{i=1}^n(\mathbf{f} * \mathbf{g})(i)

。

考虑

\sum\limits_{i=1}^{n} (\mathbf{f} * \mathbf{g})(i) = \sum\limits_{i=1}^{n} \sum\limits_{ab=i} \mathbf{f}(a)\mathbf{g}(b)

。

考虑交换求和顺序，改为先枚举

b

，可得原式即为

\sum\limits_{b=1}^{n} \sum\limits_{ab\le n} \mathbf{f}(a)\mathbf{g}(b) = \sum\limits_{b=1}^{n} \mathbf{g}(b)\sum\limits_{a=1}^{\lfloor \frac{n}{b} \rfloor} \mathbf{f}(a) = \sum\limits_{b=1}^{n} \mathbf{g}(b) \mathbf{S}(\lfloor \frac{n}{b} \rfloor)

。

所以我们得到：

\begin{aligned} \sum\limits_{i=1}^n(\mathbf{f} * \mathbf{g})(i) & \large = \sum\limits_{b=1}^{n} \mathbf{g}(b) \mathbf{S}(\lfloor \frac{n}{b} \rfloor) \\ \sum\limits_{i=1}^n(\mathbf{f} * \mathbf{g})(i) & = \mathbf{g}(1) \mathbf{S}(n) + \sum\limits_{b=2}^{n} \mathbf{g}(b) \mathbf{S}(\lfloor \frac{n}{b} \rfloor) \\ \mathbf{g}(1) \mathbf{S}(n) & = \sum\limits_{i=1}^n(\mathbf{f} * \mathbf{g})(i) - \sum\limits_{b=2}^{n} \mathbf{g}(b) \mathbf{S}(\lfloor \frac{n}{b} \rfloor) \end{aligned}

所以我们只要能快速求出

\mathbf{g}

和

\mathbf{f} * \mathbf{g}

的前缀和，就可以依据这个柿子递归地求出

\mathbf{S}(n)

了。

时间复杂度

数论分块的时候我们知道，对于

n

以内不同的

i

，

\displaystyle\left\lfloor \frac{n}{i} \right\rfloor

的取值最多有

\sqrt{n}

种，又因为

\displaystyle\left\lfloor \frac{\left\lfloor \frac{n}{i} \right\rfloor}{j}\right\rfloor = \left\lfloor \frac{n}{ij} \right\rfloor

，所以：

对于每次递归时计算的

\mathbf{S}(n)

，需要

O(\sqrt{n})

的复杂度，所以我们可以列出一下时间复杂度的柿子：

O\left( \sum\limits_{i=1}^{\sqrt{n}} \sqrt{i} + \sum\limits_{i=1}^{\sqrt{n}} \sqrt{\frac{n}{i}}\right)

这个柿子可以使用积分求出其近似值：

O\left(\int_{1}^{\sqrt{n}} \sqrt{x}\cdot dx + \int_{1}^{\sqrt{n}} \sqrt{\frac{n}{x}}\cdot dx \Bigg) = O\Bigg(\frac{2}{3}\sqrt{n}^{\frac{3}{2}} + \sqrt{n}\cdot 2\sqrt{n}^{\frac{1}{2}} \right) = O(n^{\frac{3}{4}})

然而这样做其实还不够优秀，假设我们提前预处理前

n^c

处的

\mathbf{f}

的值，我们能得到以下的复杂度：

O\Bigg(n^c + \int_{1}^{n^{1-c}} \sqrt{\frac{n}{x}} \cdot dx \Bigg) = O\Bigg(n^c + \sqrt{n}\cdot 2n^{\frac{1}{2}(1-c)} \Bigg) = O(n^c + n^{1-\frac{1}{2}c})

此时，我们令

c = 1-\frac{1}{2}c

，解得

c=\frac{2}{3}

，这样我们得到了杜教筛的时间复杂度下界：

O(n^{\frac{2}{3}})

。

CPP

int getS(int x) {
    int res = calc(x); // \sum_{i=1}^{x} (f*g)(i)
    for (int i = 2, r; i <= x; i = r + 1) {
        r = x / (x / i);
        res -= sumg(i, r) * getS(x / i);
        i = r + 1;
    }
    res /= g(1);
    return res;
}

Ⅰ. 线性基

本质上是对二进制的每一位做模

2

意义下的高斯消元，消元之后最多只有

\log V

行，矩阵中的所有非零行向量之间线性无关，所以线性基中的所有非零行向量构成了一组基底。

CPP

struct Line_Basis {
    ll s[64];
    int tot, cntdf;
    Line_Basis() {
        tot = cntdf = 0;
        memset(s, 0, sizeof(s));
    }
    bool insert(ll x) {
        for (int i = 63; i >= 0; i--) {
            if ((x >> i) & 1) {
                if (!s[i]) {
                    s[i] = x;
                    tot++;
                    return true;
                }
                else {
                    x ^= s[i];
                }
            }
        }
        cntdf++;
        return false;
    }
    ll qmax() {
        ll res = 0;
        for (int i = 63; i >= 0; i--) {
            if ((res >> i) & 1) {
                continue;
            } else {
                res ^= s[i];
            }
        }
        return res;
    }
    void init_qkth() {
        for (int i = 0; i <= 63; i++) {
            for (int j = 0; j < i; j++) {
                if ((s[i] >> j) & 1) {
                    s[i] ^= s[j];
                }
            }
        }
    }
    ll qkth(ll k) {   // 查询线性基中所有基底的异或第 k 小
        if (cntdf) {
            if (k == 1) {
                return 0;
            }
            k--;
        }
        if (k > (1ll << tot) - 1) {
            return -1;
        }
        
        ll res = 0;
        for (int i = 0; i <= 63; i++) {
            if (s[i]) {
                if (k & 1) {
                    res ^= s[i];
                }
                k >>= 1;
            }
        }
        return res;
    }
} LB;

Ⅰ. 拉格朗日插值

给定

n+1

个横坐标不同的点，求一个

n

次多项式在其他位置的取值，直接高斯消元法算多项式系数的时间复杂度是

O(n^3)

的，有没有更快的方法呢。

有，就是拉格朗插值法。

前置知识

首先由一个显然的结论，若

a

是整数，则有

x \equiv a \pmod{x-a}

根据同余的性质，若

k

是整数，则有

x^k \equiv a^k \pmod{x-a}

于是可以进一步得出结论，若

f(x)

是关于

x

的多项式，则有

f(x) \equiv f(a) \pmod{x-a}

结论推导

设给定的

n+1

个点的横坐标分别为

x_0 , x_1 ,\cdots ,x_{n}

，根据上述结论，则有同余方程组

\left\{\begin{aligned} f(x) &\equiv f(x_0) \pmod{x-x_0} \\ f(x) &\equiv f(x_1) \pmod{x-x_1} \\ &\cdots \\ f(x) &\equiv f(x_n) \pmod{x-x_n} \\ \end{aligned} \right.

要得到

f(x)

的表达式，实际上就是解这个同余方程组，这就很自然地让我们联想到了中国剩余定理。

设

N = \prod\limits_{i=0}^{n} (x-x_i)

，则对于第

i

个同余式的基向量就是

\boldsymbol{e_i} = \frac{N}{x-x_i} \left(\frac{N}{x-x_i}\right)^{-1}_{\bmod x-x_i} = \prod\limits_{j\neq i} \frac{x-x_j}{x_i - x_j}

所以用中国剩余定理合并起来就是

f(x) = \sum\limits_{i=0}^{n} f(x_i) \boldsymbol{e_i} = \sum\limits_{i=0}^{n} f(x_i) \prod\limits_{j\neq i} \frac{x-x_j}{x_i - x_j}

这样，我们只需要

O(n^2)

的时间复杂度便可以求出

f(x)

在其他位置的取值了，有一些题还有一些性质，可以做到

O(n\log n)

甚至

O(n)

。

一个例题

求

S_k(n) = \sum\limits_{i=0}^{n} i^k

，

1\le n \le 10^9 , 1\le k \le 10^6

。

根据初中数学知识，我们知道

S_1(n) = \frac{n(n+1)}{2} , S_2(n) = \frac{n(n+1)(2n+1)}{6} ,S_3(n) = \frac{n^2(n+1)^2}{4}

，这些分别是关于

n

的

2,3,4

次多项式。

于是我们猜想

S_k(n)

一定能表示成关于

n

的

k+1

次多项式。

考虑第二类斯特林数，对通常幂进行转化

\begin{aligned} i^k = \sum\limits_{j=0}^{k} \binom{i}{j} \begin{Bmatrix}k\\j\end{Bmatrix} j! = \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} i^{\underline{j}} \end{aligned}

带入

S_k(n)

中可得

\begin{aligned} &\sum_{i=0}^{n} i^k \\ =& \sum\limits_{i=0}^{n} \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} i^{\underline{j}} \\ =& \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} \sum\limits_{i=j}^{n} i^{\underline{j}} \\ =& \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} j!\sum\limits_{i=j}^{n} \binom{i}{j} \\ =& \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} j!\sum\limits_{i=0}^{n-j} \binom{i+j}{j} \\ =& \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} j!\binom{n+1}{j+1} \\ =& \sum\limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} \frac{(n+1)^{\underline{j+1}}}{j+1} \end{aligned}

由此，我们证明了

S_k(n)

是关于

n

的

k+1

次多项式。

所以我们只需要求出

S_k(1) ,S_k(2) , \cdots , S_k(k+2)

这

k+2

个点的点值，然后拉格朗日插值一下，就可以求出

S_k(n)

了。

那么拉格朗日插值的式子就是

S_k(n) = \sum\limits_{i=1}^{k+2} S_k(i) \prod\limits_{j\neq i} \frac{n-j}{i-j}

然后对于

\prod n-j

预处理一下，发现

\prod i-j

实际上一个数的阶乘乘上

(-1)

的一个数次方，分别算一下就可以

O(k\log k)

了。

Ⅰ. 组合数的基本性质

排列数与组合数

杨辉三角、组合数的一些恒等式、二项式定理

定义牛顿二项式系数

\binom{r}{n} = \left\{\begin{aligned} &0 &(n<0) \\ &1 &(n=0) \\ &\frac{r(r-1)\cdots(r-n+1)}{n!} &(n>0) \end{aligned} \right.

注意其中的

n\in \mathbb{Z}

，而

r\in \mathbb{R}

，所以牛顿二项式系数没有组合意义，当

r,n

均为非负整数时，

\binom{r}{n}

在数值上等于

C_{r}^{n}

。

牛顿二项式定理

(x+y)^\alpha = \sum\limits_{n=0}^{\infty} \binom{\alpha}{n} x^n y^{\alpha - n}

其中

\alpha \in \mathbb{R}

。（一种可行的证明是使用泰勒级数将左式展开）

组合数的上指标翻转 $\binom{r}{n} = (-1)^{n}\binom{n - r - 1}{n}$

范德蒙德卷积

\sum_{i=0}^{k}\binom{n}{i}\binom{m}{k - i} = \binom{n + m}{k}

卡特兰数

想象成在二维坐标网格上从

(0,0)

沿对角线游走到

(n, 0)

的方案数，不能走到第三象限。

考虑容斥即可得到方案数为

\binom{2n}{n} - \binom{2n}{n - 1}

。

利用容斥原理设计的 dp 举例：

带标号有向无环图计数

考虑设 $f_n$ 代表 $n$ 的点带标号有有向无环图数量。

注意到有向无环图中一定会有至少一个入度为 $0$ 的点。设 $S_i$ 代表结点 $i$ 入度为 $0$ 的 $\text{DAG}$ 集合，则 $f_n = | S_1 \cup S_2 \cup \cdots \cup S_n|$ 。对 $f_n$ 进行容斥，枚举钦定入度为 $0$ 的点的个数 $i$ ，考虑每个入度为 $0$ 的点向剩余的 $n - i$ 个点是否连边，能推出如下等式
$\begin{aligned} f_n = \sum\limits_{i = 1}^{n} (-1)^{i - 1} \binom{n}{i} 2^{(n - i)i} f_{n - i} \end{aligned}$
直接暴力递推能够做到 $O(n^{2})$ 的时间复杂度。

注意到，如果令 $g_i = \displaystyle{(-1)^{i - 1}\binom{n}{i}2^{(n - i)i}}$ ，则 $\displaystyle{f_n = \sum\limits_{i = 1}^{n} f_{i}g_{n - i}}$ ， $f_0 = 1$ ，是半在线卷积的标准形式，使用分治 FFT 或多项式求逆计算 $f$ 可分别做到 $O(n\log^{2}n)$ 和 $O(n\log n)$ 的优秀时间复杂度。

形式一

若
$\begin{equation} f(n) = \sum\limits_{i = 0}^{n} \binom{n}{i} g(i) \tag{2.1} \end{equation}$
则有
$\begin{equation} g(n) = \sum\limits_{i = 0}^{n} \binom{n}{i}(-1)^{n - i}f(i) \tag{2.2} \end{equation}$
**证明：**将等式 $2.1$ 带入式 $2.2$ 中，则 $2.2$ 的右边可化为
$\begin{aligned} &\sum\limits_{i = 0}^{n} \binom{n}{i}(-1)^{n - i}\sum\limits_{j = 0}^{i}\binom{i}{j}g(j) \\ = &\sum\limits_{j = 0}^{n}g(j)\sum_{i = j}^{n} \binom{n}{i}\binom{i}{j}(-1)^{n - i} \\ = &\sum\limits_{j = 0}^{n}g(j)\sum_{i = j}^{n} \binom{n}{j}\binom{n - j}{i - j}(-1)^{n - i}\\ = &\sum\limits_{j = 0}^{n} \binom{n}{j}g(j)\sum_{i = j}^{n} \binom{n - j}{i - j}(-1)^{n - i}\\ = &\sum\limits_{j = 0}^{n} \binom{n}{j}g(j)\sum_{k = 0}^{n - j} \binom{n - j}{k}(-1)^{n - j - k}\\ = &\sum\limits_{j = 0}^{n} \binom{n}{j}g(j)\left[n - j = 0\right] \\ = &\text{ }g(n) \end{aligned}$
所以式 $2.2$ 左边等于右边，等式成立。
形式二

若
$\begin{equation} f(n) = \sum\limits_{i = n}^{m} \binom{i}{n} g(i) \tag{2.3} \end{equation}$
则有
$\begin{equation} g(n) = \sum\limits_{i = n}^{m} \binom{i}{n}(-1)^{i - n}f(i) \tag{2.4} \end{equation}$
**证明：**方法与形式一类似，将 $2.3$ 带入 $2.4$ ，则 $2.4$ 的右边可化为
$\begin{aligned} &\sum\limits_{i = n}^{m}\binom{i}{n} (-1)^{i - n} \sum\limits_{j = i}^{m} \binom{j}{i}g(j) \\ =&\sum\limits_{j = n}^{m} g(j) \sum\limits_{i = n}^{j}\binom{j}{i}\binom{i}{n}(-1)^{i - n} \\ =&\sum\limits_{j = n}^{m} g(j) \sum\limits_{i = n}^{j}\binom{j}{n}\binom{j - n}{i - n}(-1)^{i - n} \\ =&\sum\limits_{j = n}^{m} \binom{j}{n} g(j) \sum\limits_{i = n}^{j}\binom{j - n}{i - n}(-1)^{i - n} \\ =&\sum\limits_{j = n}^{m} \binom{j}{n} g(j) \sum\limits_{k = 0}^{j - n}\binom{j - n}{k}(-1)^{k} \\ =&\sum\limits_{j = n}^{m} \binom{j}{n} g(j)\left[j - n = 0\right]\\ =&\text{ }g(n) \end{aligned}$
所以式 $2.4$ 左边等于右边，等式成立。

概率生成函数 PGF

对于离散的概率生成函数

\begin{aligned} f_X(x) &= \sum_{k} P(X=k)x^{k} \\ E(X) &= \sum_{k}k\cdot P(X=k) = f'_{X}(1) \\ E(X^2) &= \sum_{k} k^{2}P(X=k) = \sum_{k}[k(k - 1) + k]P(X=k) = f''_{X}(1) + f'_{X}(1) \end{aligned}

考虑怎么求

E(x^{n})

，由于

\begin{aligned} f_{X}(e^{x}) &= \sum_{k}P(X=k)e^{kx} \\ &= \sum_{k}P(X=k)\sum_{n}\frac{(kx)^n}{n!} \\ &= \sum_{n}\frac{x^{n}}{n!}\sum_{k} P(X=k)k^{n} \\ &= \sum_{n}\frac{E(X^{n})}{n!}x^{n} \end{aligned}

这称为随机变量

X

的矩母函数，由此可见

E(x^{n}) = n![x^{n}]f_{X}(e^{x})

，考虑怎么求

f_X(e^{x})

的各项系数。

若

f_{X}(x)

是无限项的，需要求其封闭形式；若

f_{X}(x)

是有限项的，考虑求

\begin{aligned} \sum_{n}E(X^{n})x^{n} &= \sum_{n}\sum_{k} P(X=k)k^{n}x^{n} \\ &= \sum_{n}\sum_{k}f_{k}k^{n}x^{n} \\ &= \sum_{k}f_{k}\sum_{n}(kx)^{n} \\ &= \sum_{k} \frac{f_{k}}{1 - kx} \end{aligned}

使用分治 FFT 维护分子分母，最后多项式求逆即可求出，时间复杂度

O(n\log^{2}n)

。

下面我们来一道例题，一个歌唱王国的加强版。

字符集为 $\Sigma$ ，打出第 $i$ 个字符的概率为 $p_{i}$ ，给出一个字符串 $s$ ，求后缀第一次出现字符串 $s$ 的期望打字次数 $E(s)$ 。

令

f_{k}

代表打了

k

个字符还没停的概率，

g_k

代表打了

k

个字符恰好停的概率。

由于

f_{k} = \sum_{j=k+1}g_{j} = f_{k + 1} + g_{k + 1}

，即

\begin{aligned} 1 + xf(x) = f(x) + g(x)\ \ \ \ \ \ (1) \end{aligned}

考虑打了

p

个字符还没停，并且钦定在后面完整地打出一个字符串

t

的概率，用两种不同的形式表达，即

\begin{aligned} f_{p} \prod_{i = 1}^{|t|}p_{t_{i}} = \sum_{k\in \text{border}(t)} g_{p+k}\prod_{i = k + 1}^{|t|}p_{t_{i}} \end{aligned}

写成生成函数的形式，即

\begin{aligned} f(x)\cdot x^{|t|}\prod_{i=1}^{|t|}p_{t_{i}} = g(x) \sum_{k\in \text{border}(t)} x^{|t|-k}\prod_{i=k+1}^{|t|}p_{t_{i}} \ \ \ \ \ (2) \end{aligned}

将

(1)

式带入

(2)

式中，化简可得

\begin{aligned} g(x) = \frac{\prod\limits_{i=1}^{|t|}p_{t_{i}}}{(1-x)\sum\limits_{k\in \text{border(t)}}x^{-k}\prod\limits_{i=k+1}^{|t|}p_{t_i} + \prod_{i=1}^{|t|}p_{t_{i}}} \end{aligned}

求导带入

x=1

即可得到

\begin{aligned} E(s) = g'(1) = \sum\limits_{k\in \text{border}(t)}\prod_{i=1}^{k}\frac{1}{p_{t_{i}}} \end{aligned}

先放代码。

CPP

struct Twelve_count_method {
    static mint Subtask1(int n, int m) {   // 球之间互不相同，盒子之间互不相同，无放球限制
        return (mint)m ^ n;
    }
    static mint Subtask2(int n, int m) {   // 球之间互不相同，盒子之间互不相同，每个盒子至多装一个
        return n > m ? 0 : C(m, n) * fac[n];
    }
    static mint Subtask3(int n, int m) {   // 球之间互不相同，盒子之间互不相同，每个盒子至少装一个球
        return Subtask6(n, m) * fac[m];
    }
    static mint Subtask4(int n, int m) {   // 球之间互不相同，盒子全部相同，无放球限制
        vector<mint> f(m + 1), g(m + 1);
        for (int i = 0; i <= m; i++) {
            f[i] = ((i & 1) ? (Mod - 1) : 1) * invf[i];
            g[i] = ((mint)i ^ n) * invf[i];
        }
        auto h = convolution(f, g);
        
        mint res = 0;
        for (int i = 0; i <= m; i++) {
            res += h[i]; 
        }
        return res;
    }
    static mint Subtask5(int n, int m) {   // 球之间互不相同，盒子全部相同，每个盒子至多装一个球
        return n > m ? 0 : 1;
    }
    static mint Subtask6(int n, int m) {   // 球之间互不相同，盒子全部相同，每个盒子至少装一个球
        vector<mint> f(m + 1), g(m + 1);
        for (int i = 0; i <= m; i++) {
            f[i] = ((i & 1) ? (Mod - 1) : 1) * invf[i];
            g[i] = ((mint)i ^ n) * invf[i];
        } 
        auto h = convolution(f, g);
        return h[m];
    }
    static mint Subtask7(int n, int m) {   // 球全部相同，盒子之间互不相同，无放球限制
        return C(n + m - 1, m - 1);
    }
    static mint Subtask8(int n, int m) {   // 球全部相同，盒子之间互不相同，每个盒子至多装一个球
        return C(m, n);
    }
    static mint Subtask9(int n, int m) {   // 球全部相同，盒子之间互不相同，每个盒子至少装一个球
        return C(n - 1, m - 1);
    }
    static mint Subtask10(int n, int m) {  // 球全部相同，盒子全部相同，无放球限制
        vector<mint> f(n + 1, (mint)0);
        for (int i = 1; i <= m; i++) {
            for (int j = 1; i * j <= n; j++) {
                f[i * j] += inv[j];
            }
        }
        f = polyexp(f, n + 1);
        return f[n];
    }
    static mint Subtask11(int n, int m) {  // 球全部相同，盒子全部相同，每个盒子至多装一个球
        return n > m ? 0 : 1;
    }
    static mint Subtask12(int n, int m) {  // 球全部相同，盒子全部相同，每个盒子至少装一个球
        if (n < m) {
            return 0;
        }
        return Subtask10(n - m, m);
    }
};

第六重——第二类斯特林数

**求方案数：**将 $n$ 个带标号的小球放入 $m$ 个不带标号的盒子、要求盒子非空。

1. 递推式

设

\displaystyle{n \brace m}

表示上述方案数，讨论

n

号小球是否单独放在一个新的盒子里，将

n

个小球的情况与

n - 1

个小球的情况建立映射关系，能得到递推式

\begin{equation} {n \brace m} = {n - 1 \brace m - 1} + m {n - 1 \brace m} \tag{6.1} \end{equation}

2. 通项式

根据组合意义，能够得到

\begin{equation} m^{n} = \sum\limits_{i = 0}^{m} \binom{m}{i} {n \brace i} i! \label{XX} \tag{6.2} \end{equation}

**等式左边的含义：**将

n

个带标号的小球，放到

m

个带标号的盒子中，盒子可以空的方案数；

**等式右边的含义：**先枚举非空盒子的个数

i

，然后计算

n

个带标号的小球放入

i

个带标号的盒子、要求盒子非空的方案数，与选出

i

个盒子的方案数相乘，求和后与等式左边的含义相同。

令

f(i) = i^{n}, g(i) = \displaystyle{n \brace i} i!

，则等式

6.2

可写作

\begin{aligned} f(m) = \sum\limits_{i = 0} ^ {m} \binom{m}{i} g(i) \end{aligned}

由二项式反演，得

\begin{aligned} g(m) = \sum\limits_{i = 0}^{m} \binom{m}{i} (-1)^{m - i}f(i) \end{aligned}

展开后移项能够得到通项式

\begin{equation} {n \brace m} = \frac{1}{m!}\sum\limits_{i = 0}^{m} \binom{m}{i}(-1)^{m - i}i^{n} \tag{6.3} \end{equation}

3. 行的计算

显然直接用递推式暴力计算需要 $O(n^{2})$ 的时间复杂度，这样多耗费了很多时间代价去计算前 $n - 1$ 行的第二类斯特林数，那有没有办法不计算前 $n - 1$ 行的值就能得到第 $n$ 行呢，请看下文。

将通项式中的组合数展开可以得到

\begin{equation} {n \brace m} = \sum\limits_{i = 0}^{m} \frac{(-1)^{m - i}}{(m - i)!}\cdot\frac{i^{n}}{i!} \tag{6.4} \end{equation}

令

F_i = \displaystyle\frac{(-1)^{i}}{i!}, G_i = \displaystyle\frac{i^{n}}{i!}

，容易发现，第

n

行的斯特林数数列

\{S_{n,m}\}

就是

F

与

G

的卷积，可以利用快速数论变换进行优化，时间复杂度可以做到

O(n\log n)

。

4. 列的计算

考虑指数生成函数

\displaystyle F(x) = \sum\limits_{n = 1}^{\infty} \frac{x^{n}}{n!}

，通过生成函数的学习可以知道

F^{k}(x)

是

i

个有标号小球放到

k

个有标号盒子中，且盒子不能为空的指数型生成函数，那么只需要将对应项的系数除以

k!

，即可得到第二类斯特林数。即

\begin{aligned} {i \brace k} = \frac{i!\left[x^{i}\right]F^{k}(x)}{k!} \end{aligned}

使用多项式快速幂计算出

F^{k}(x)

即可在

O(n\log n)

的时间复杂度内求出某一列的前

n

个第二类斯特林数。

5. 应用

如果将等式

6.2

的组合数展开，写作下降幂的形式

\begin{equation} m^n = \sum\limits_{i = 0}^{m} {n \brace i} m^{\underline{i}} \end{equation}

由于只有

n

个球，所以非空的盒子不可能超过

n

个，所以上式也可写作

\begin{equation} m^n = \sum\limits_{i = 0}^{\min(n, m)} {n \brace i} m^{\underline{i}} \end{equation}

考虑求自然数的

k

次方和

\sum\limits_{i = 1}^{n} i^{k}

，直接做是

O(n\log k)

的，将

i^{k}

通过上式展开

\begin{aligned} \sum\limits_{i = 0}^{n} i^{k} &= \sum\limits_{i = 0}^{n} \sum\limits_{j = 0}^{\min(i, k)} {k \brace j}i^{\underline{j}} \\ &= \sum\limits_{j = 0}^{k} {k \brace j} \sum\limits_{i = j}^{n} i^{\underline{j}} \\ &= \sum\limits_{j = 0}^{k} {k \brace j} j! \sum\limits_{i = j}^{n} \binom{i}{j} \\ &= \sum\limits_{j = 0}^{k} {k \brace j} j! \binom{n + 1}{j + 1} \\ &= \sum\limits_{j = 0}^{k} {k \brace j} \frac{(n + 1)^{\underline{j + 1}}}{j + 1} \\ \end{aligned}

发现时间复杂度的瓶颈为求出第

k

行的第二类斯特林数，通过**「3. 行的计算」**中的方法，可以做到

O(k \log k)

。（题目链接）

如果模数不是 NTT 模数，可以学习任意模数 NTT，也可以用拉格朗日插值来做。由于是多项式技巧，这里不展开写了，详见我的这篇文章。

六. 计算几何

Ⅰ. 向量基础运算

CPP

const double eps = 1e-8;
const double pi = acos(-1);

bool dcmp(double x, double y = 0) { 
	return fabs(x - y) <= eps;
}

struct Pt {
	double x, y;
	Pt(double xx = 0, double yy = 0): x(xx), y(yy) {}
	friend Pt operator + (const Pt& a, const Pt& b) {
		Pt res(a.x + b.x, a.y + b.y);
		return res;
	}
	friend Pt operator - (const Pt& a, const Pt& b) {
		Pt res(a.x - b.x, a.y - b.y);
		return res;
	}
	friend Pt operator * (const Pt& a, const double& k) {
		Pt res(a.x * k, a.y * k);
		return res;
	}
	friend Pt operator / (const Pt& a, const double& k) {
		Pt res(a.x / k, a.y / k);
		return res;
	}
};

double dist(const Pt& a, const Pt& b) {
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 
}
double dot(const Pt& a, const Pt& b) {
	return a.x * b.x + a.y * b.y;
}
double cross(const Pt& a, const Pt& b) {
	return a.x * b.y - b.x * a.y;
}

Andrew 算法求凸包模板。

CPP

Poly andrew(vector<Pt> p, int n) {
	sort(p.begin(), p.end(), [&](auto u, auto v) -> bool {
		if (dcmp(u.x, v.x)) {
			return u.y > v.y;
		}
		return u.x < v.x;
	});
	int tp = 0;
	vector st(n, 0);
	vector used(n, false);
	st[++tp] = 0;
	for (int i = 1; i < n; i++) {		// 求下凸壳
		while (tp >= 2 && cross(p[st[tp]] - p[st[tp - 1]], p[i] - p[st[tp]]) <= 0) {
			used[st[tp--]] = false;
		}
		used[i] = true;
		st[++tp] = i;
	}
	// 下凸壳最左和最右分别为 p[0] 和 p[n - 1]

	int R = tp;
	for (int i = n - 2; i >= 0; i--) {	// 求上凸壳
		if (!used[i]) {
			while (tp > R && cross(p[st[tp]] - p[st[tp - 1]], p[i] - p[st[tp]]) <= 0) {
				used[st[tp--]] = false;
			}
			used[i] = true;
			st[++tp] = i;
		}
	}
	// st[1] 和 st[tp] 都为 p[0]
	Poly res;
	for (int i = 2; i <= tp; i++) {
		res.pts.push_back(p[st[i]]);
	}
	return res;
}

Ⅰ. 多项式求逆

多项式求逆原理

设

G(x)

为

F(x)

模

x^n

意义下的逆，则

F(x)G(x) \equiv 1 \pmod{x^n}

设

G'(x)

为

F(x)

模

x^{n/2}

意义下的逆，则

F(x)G'(x) \equiv 1 \pmod{x^{n/2}}

联立上述二式，得

\begin{aligned} G(x) &\equiv G'(x) &\pmod{x^{n/2}} \\ (G(x) - G'(x))^2 &\equiv 0 &\pmod{x^n} \\ G(x)^2 - 2G(x)G'(x) + G'(x)^2 &\equiv 0 &\pmod{x^n} \\ F(x)G(x)^2 - 2F(x)G(x)G'(x) + F(x)G'(x)^2 &\equiv 0 &\pmod{x^n} \\ G(x) - 2G'(x) + F(x)G'(x)^2 &\equiv 0 &\pmod{x^n} \\ G(x) &\equiv G'(x)(2 - F(x)G'(x)) &\pmod{x^n} \\ \end{aligned}

多项式

\ln

原理

设

G(x) = \ln A(x)

，则两边同时求导得

\begin{aligned} \frac{\text{d}}{\text{d}x} G(x) &= \frac{\text{d}}{\text{d}A}\ln A(x) \frac{\text{d}}{\text{d}x} A(x) \\ \frac{\text{d}}{\text{d}x} G(x) &= \frac{\frac{\text{d}}{\text{d}x} A(x)}{A(x)} \end{aligned}

直接对

A(x)

求导和求逆，把两个东西乘起来再进行一次不定积分，就可以得到

G(x)

了。

多项式

\exp

原理

设

B(x) \equiv e^{A(x)} \pmod{x^n}

，两边取对数得

\begin{aligned} \ln B(x) &\equiv A(x) &\pmod{x^n} \\ \ln B(x) - A(x) &\equiv 0 &\pmod{x^n} \\ \end{aligned}

设

F(z)

是定义域为多项式的函数，且

F(G(x)) = \ln G(x) - A(x)

。

设

B_0(x)

满足

\ln B_0(x) - A(x) \equiv 0 \pmod{x^{n/2}}

，即

F(B_0(x)) \equiv 0 \pmod{x^{n/2}}

。

根据牛顿迭代，若

B(x) = B_0(x) - \frac{F(B_0(x))}{F'(B_0(x))}

则

F(B(x)) \equiv 0 \pmod{x^n}

一定成立。

而我们化简一下上式就有

B(x) = B_0(x) - \frac{\ln B_0(x) - A(x)}{\frac{1}{B_0(x)}} = B_0(x)(1-\ln B_0(x) + A(x))

这样我们就可以从

\bmod x^{n/2}

意义下的

\exp

求出

\bmod x^n

意义下的

\exp

，时间复杂度是

T(n) = T(\frac{n}{2}) + O(n\log n) = O(n\log n)

多项式卷积 [convolution] $O(n\log n)$
多项式加法/减法 [polyadd/polysub] $O(n)$
多项式求导/积分 [derivation/integrate] $O(n)$
多项式求逆 [polyinv] $O(n \log n)$
多项式求对数 [polyln] $O(n \log n)$
多项式 $\exp$ [polyexp] $O(n \log n)$
多项式快速幂 [polyksm] $O(n \log n)$

CPP

namespace Polynomial {
    const int Mod = 998244353;
    const int G = 3;
    
    template<int mod>
    class Modint {
        private:
            unsigned int x;
        public:
            Modint() = default;
            Modint(unsigned int x): x(x) {}
        friend istream& operator >> (istream& in, Modint& a) {return in >> a.x;}
        friend ostream& operator << (ostream& out, Modint a) {return out << a.x;}
        friend Modint operator + (Modint a, Modint b) {return (a.x + b.x) % mod;}
        friend Modint operator - (Modint a, Modint b) {return (a.x - b.x + mod) % mod;}
        friend Modint operator * (Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
        friend Modint operator / (Modint a, Modint b) {return a * ~b;}
        friend Modint operator ^ (Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
        friend Modint operator ~ (Modint a) {return a ^ (mod - 2);}
        friend Modint operator - (Modint a) {return (mod - a.x) % mod;}
        friend Modint& operator += (Modint& a, Modint b) {return a = a + b;}
        friend Modint& operator -= (Modint& a, Modint b) {return a = a - b;}
        friend Modint& operator *= (Modint& a, Modint b) {return a = a * b;}
        friend Modint& operator /= (Modint& a, Modint b) {return a = a / b;}
        friend Modint& operator ^= (Modint& a, int b) {return a = a ^ b;}
        friend Modint& operator ++ (Modint& a) {return a += 1;}
        friend Modint operator ++ (Modint& a, int) {Modint x = a; a += 1; return x;}
        friend Modint& operator -- (Modint& a) {return a -= 1;}
        friend Modint operator -- (Modint& a, int) {Modint x = a; a -= 1; return x;}
        friend bool operator == (Modint a, Modint b) {return a.x == b.x;}
        friend bool operator != (Modint a, Modint b) {return !(a == b);}
    };
    typedef Modint<Mod> mint;

    void init_convo(vector<int>& rev, int& lim, int n, int m) {
        int s = 0;
        for (lim = 1; lim <= n + m; lim <<= 1, s++);
        rev.resize(lim);
        for (int i = 0; i < lim; i++) {
            rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (s - 1));
        }
    }

    void NTT(vector<mint>& f, vector<int>& rev, int lim, int type) {
        f.resize(lim, 0);
        for (int i = 0; i < lim; i++) {
            if (i < rev[i]) {
                swap(f[i], f[rev[i]]);
            }
        }
        for (int i = 1; i < lim; i <<= 1) {
            mint mul = (mint)G ^ ((Mod - 1) / (i << 1));
            if (type == -1) {
                mul = ~mul;
            }
            for (int j = 0; j < lim; j += (i << 1)) {
                mint w = 1;
                for (int k = 0; k < i; k++, w *= mul) {
                    mint x = f[j + k], y = w * f[j + k + i];
                    f[j + k] = x + y;
                    f[j + k + i] = x - y;
                }
            }
        }
    }

    vector<mint> convolution(vector<mint> f, vector<mint> g, int k1, int k2, mint (*calc)(mint x, mint y)) {
        int n = SZ(f) - 1, m = SZ(g) - 1, lim;
        vector<int> rev;
        init_convo(rev, lim, k1 * n, k2 * m);

        NTT(f, rev, lim, 1);
        NTT(g, rev, lim, 1);
        vector<mint> h(lim);
        for (int i = 0; i < lim; i++) {
            h[i] = calc(f[i], g[i]);
        }
        NTT(h, rev, lim, -1);
        mint invlim = ~(mint)lim;
        for (int i = 0; i < lim; i++) {
            h[i] = h[i] * invlim;
        }
        h.resize(k1 * n + k2 * m + 1);
        return h;
    }
    vector<mint> convolution(const vector<mint>& f, const vector<mint>& g) {
        return convolution(f, g, 1, 1, [](mint x, mint y) -> mint {
            return x * y;
        });
    }

    vector<mint> derivation(vector<mint> f) {
        int n = SZ(f);
        for (int i = 1; i < n; i++) {
            f[i - 1] = f[i] * i;
        }
        f.resize(n - 1);
        return f;
    }
    vector<mint> integrate(vector<mint> f) {
        int n = SZ(f);
        f.resize(n + 1, 0);
        for (int i = n - 1; i >= 0; i--) {
            f[i + 1] = f[i] / (i + 1);
        }
        f[0] = 0;
        return f;
    }

    vector<mint> polyadd(const vector<mint>& f, const vector<mint>& g) {
        int n = SZ(f), m = SZ(g);
        int mx = max(n, m), mn = min(n, m);
        vector<mint> h(mx);
        for (int i = 0; i < mn; i++) {
            h[i] = f[i] + g[i];
        }
        for (int i = mn; i < mx; i++) {
            h[i] = (n > m) ? f[i] : g[i];
        }
        return h;
    }
    vector<mint> polysub(const vector<mint>& f, const vector<mint>& g) {
        int n = SZ(f), m = SZ(g);
        int mx = max(n, m), mn = min(n, m);
        vector<mint> h(mx);
        for (int i = 0; i < mn; i++) {
            h[i] = f[i] - g[i];
        }
        for (int i = mn; i < mx; i++) {
            h[i] = (n > m) ? f[i] : -g[i];
        }
        return h;
    }

    vector<mint> polyinv(vector<mint> f, int n) {   // 1 / f(x) (mod x^n)
        f.resize(n);
        if (n == 1) {
            f[0] = ~f[0];
            return f;
        }
        auto g = polyinv(f, (n + 1) >> 1);
        g = convolution(f, g, 1, 2, [](mint x, mint y) -> mint {
            return (2 - x * y) * y;
        });
        g.resize(n, 0);
        return g;
    }

    vector<mint> polyln(vector<mint> f, int n) {    // ln f(x) (mod x^n) , f[0] = 1
        f = integrate(convolution(derivation(f), polyinv(f, n)));
        f.resize(n, 0);
        return f;
    }

    vector<mint> polyexp(vector<mint> f, int n) {   // exp f(x) (mod x^n) , f[0] = 0 | Newton's Method
        f.resize(n, 0);
        if (n == 1) {
            f[0] = 1;
            return f;
        }
        auto g0 = polyexp(f, (n + 1) >> 1);
        auto g1 = polysub(polyln(g0, n), f);
        auto h = convolution(g0, g1, 1, 1, [](mint x, mint y) -> mint {
            return x * (1 - y);
        });
        h.resize(n, 0);
        return h;
    }

    vector<mint> __polyksm(vector<mint> f, int k, int n) {    // [f(x)]^{k} (mod x^n) , f[0] = 0 | exp(ln f(x))
        f = polyln(f, n);
        for (int i = 0; i < n; i++) {
            f[i] *= k;
        }
        f = polyexp(f, n);
        f.resize(n, 0);
        return f;
    }

    vector<mint> polyksm(vector<mint> f, int k, int n) {    // [f(x)]^{k} (mod x^n)
        f.resize(n, 0);
        int p = 0;
        for (int i = 0; i < n; i++) {
            if (f[i] != 0) {
                p = i;
                break;
            }
        }
        mint coef = ~f[p];
        vector<mint> g(n - p);
        for (int i = 0; i < n - p; i++) {
            g[i] = f[i + p] * coef;
        }
        g = __polyksm(g, k, n);
        
        ll d = 1ll * p * k;
        coef = (~coef) ^ k;
        fill(f.begin(), f.end(), 0);
        for (int i = n - 1; i >= d; i--) {
            f[i] = g[i - d] * coef;
        }
        return f;
    }
}
using Polynomial::convolution;
using Polynomial::Mod;
using Polynomial::mint;

CPP

namespace Polynomial {
    const int Mod[] = {469762049, 998244353, 1004535809};
    const int G = 3;
    
    template<int mod>
    class Modint {
        private:
            unsigned int x;
        public:
            Modint() = default;
            Modint(unsigned int x): x(x) {}
        unsigned int getx() { return x; }
        friend istream& operator >> (istream& in, Modint& a) {return in >> a.x;}
        friend ostream& operator << (ostream& out, Modint a) {return out << a.x;}
        friend Modint operator + (Modint a, Modint b) {return (a.x + b.x) % mod;}
        friend Modint operator - (Modint a, Modint b) {return (a.x - b.x + mod) % mod;}
        friend Modint operator * (Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
        friend Modint operator / (Modint a, Modint b) {return a * ~b;}
        friend Modint operator ^ (Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
        friend Modint operator ~ (Modint a) {return a ^ (mod - 2);}
        friend Modint operator - (Modint a) {return (mod - a.x) % mod;}
        friend Modint& operator += (Modint& a, Modint b) {return a = a + b;}
        friend Modint& operator -= (Modint& a, Modint b) {return a = a - b;}
        friend Modint& operator *= (Modint& a, Modint b) {return a = a * b;}
        friend Modint& operator /= (Modint& a, Modint b) {return a = a / b;}
        friend Modint& operator ^= (Modint& a, int b) {return a = a ^ b;}
        friend Modint& operator ++ (Modint& a) {return a += 1;}
        friend Modint operator ++ (Modint& a, int) {Modint x = a; a += 1; return x;}
        friend Modint& operator -- (Modint& a) {return a -= 1;}
        friend Modint operator -- (Modint& a, int) {Modint x = a; a -= 1; return x;}
        friend bool operator == (Modint a, Modint b) {return a.x == b.x;}
        friend bool operator != (Modint a, Modint b) {return !(a == b);}
    };

    typedef Modint<469762049> mintp0;
    typedef Modint<998244353> mintp1;
    typedef Modint<1004535809> mintp2;

    void init_convo(vector<int>& rev, int& lim, int n, int m) {
        int s = 0;
        for (lim = 1; lim <= n + m; lim <<= 1, s++);
        rev.resize(lim);
        for (int i = 0; i < lim; i++) {
            rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (s - 1));
        }
    }

    template <typename mint>
    void NTT(vector<mint>& f, vector<int>& rev, int lim, int type, int mod) {
        f.resize(lim, 0);
        for (int i = 0; i < lim; i++) {
            if (i < rev[i]) {
                swap(f[i], f[rev[i]]);
            }
        }
        for (int i = 1; i < lim; i <<= 1) {
            mint mul = (mint)G ^ ((mod - 1) / (i << 1));
            if (type == -1) {
                mul = ~mul;
            }
            for (int j = 0; j < lim; j += (i << 1)) {
                mint w = 1;
                for (int k = 0; k < i; k++, w *= mul) {
                    mint x = f[j + k], y = w * f[j + k + i];
                    f[j + k] = x + y;
                    f[j + k + i] = x - y;
                }
            }
        }
    }

    template <typename mint>
    vector<mint> convolution(vector<mint> f, vector<mint> g, int mod) {
        int n = SZ(f) - 1, m = SZ(g) - 1, lim;
        vector<int> rev;
        init_convo(rev, lim, n, m);

        NTT(f, rev, lim, 1, mod);
        NTT(g, rev, lim, 1, mod);
        vector<mint> h(lim);
        for (int i = 0; i < lim; i++) {
            h[i] = f[i] * g[i];
        }
        NTT(h, rev, lim, -1, mod);
        mint invlim = ~(mint)lim;
        for (int i = 0; i < lim; i++) {
            h[i] = h[i] * invlim;
        }
        h.resize(n + m + 1);
        return h;
    }

    ll ksm(ll x, ll y, ll mod) {
        ll res = 1;
        while (y) {
            if (y & 1) {
                res = res * x % mod;
            }
            x = x * x % mod;
            y >>= 1;
        }
        return res;
    }
    ll inv(ll x, ll mod) {
        return ksm(x, mod - 2, mod);
    }
    ll mul(ll a, ll b, ll mod){
	    return (a * b - (ll)((long double)a / mod * b) * mod + mod) % mod;
    }

    vector<int> convolution(const vector<int>& f, const vector<int>& g, int mod) {
        int n = SZ(f) - 1, m = SZ(g) - 1;
        vector res(3, vector(n + m + 1, 0));

        {
            vector<mintp0> F, G; 
            F.resize(n + 1);
            G.resize(m + 1);
            for (int i = 0; i <= n; i++) {
                F[i] = f[i];
            }
            for (int i = 0; i <= m; i++) {
                G[i] = g[i];
            }
            auto cur = convolution(F, G, Mod[0]);
            for (int i = 0; i <= n + m; i++) {
                res[0][i] = cur[i].getx();
            }
        }

        {
            vector<mintp1> F, G; 
            F.resize(n + 1);
            G.resize(m + 1);
            for (int i = 0; i <= n; i++) {
                F[i] = f[i];
            }
            for (int i = 0; i <= m; i++) {
                G[i] = g[i];
            }
            auto cur = convolution(F, G, Mod[1]);
            for (int i = 0; i <= n + m; i++) {
                res[1][i] = cur[i].getx();
            }
        }

        {
            vector<mintp2> F, G; 
            F.resize(n + 1);
            G.resize(m + 1);
            for (int i = 0; i <= n; i++) {
                F[i] = f[i];
            }
            for (int i = 0; i <= m; i++) {
                G[i] = g[i];
            }
            auto cur = convolution(F, G, Mod[2]);
            for (int i = 0; i <= n + m; i++) {
                res[2][i] = cur[i].getx();
            }
        }
        
        vector<int> h;
        h.resize(n + m + 1);
        ll p0 = Mod[0], p1 = Mod[1], p2 = Mod[2];
        ll k0 = inv(p1, p0), k1 = inv(p0, p1);
        ll ip0 = inv(p0, p2), ip1 = inv(p1, p2);
        for (int i = 0; i <= n + m; i++) {
            ll a0 = res[0][i], a1 = res[1][i], a2 = res[2][i];
            ll m = p0 * p1;
            ll a3 = (mul(a0, mul(k0, p1, m), m) + mul(a1, mul(k1, p0, m), m)) % m;
            ll a4 = mul(mul(((a2 - a3) % p2 + p2) % p2, ip0, p2), ip1, p2);
            h[i] = (mul(mul(a4, p0, mod), p1, mod) + a3) % mod; 
        }
        return h;
    }
}
using Polynomial::convolution;

CPP

mt19937 mrnd(std::chrono::steady_clock::now().time_since_epoch().count());
int rnd(int l, int r) {
    return mrnd() % (r - l + 1) + l;
}
double rnd01() {
    return mrnd() * 1.0 / UINT32_MAX;
}

CPP

struct Line {
    Line(int l, int r, int v): l(l), r(r), v(v) {}
    int l, r, v;
};
struct Scan_Line {
    Seg_T tr;
    vector<Line> line[MAXN];
    void add(int l0, int r0, int v) {
        line[l0].push_back(Line(l0, r0, v));
        line[r0 + 1].push_back(Line(l0, r0, inv(v)));
    }
    int solve(int n) {
        int res = 0;
        tr.build(1, 1, n);
        for (int i = 1; i <= n; i++) {
            for (auto [l, r, v] : line[i]) {
                tr.upd(1, 1, n, l, r, v);
            }
            res = (res + tr.query(1, 1, n, i, n)) % Mod;
        }
        return res;
    }
} scan;

CPP

namespace Fwt {
    template<typename T>
    void or_fwt(vector<T>& a, int lim, int type) {
        a.resize(lim, 0);
        for (int i = 1; i < lim; i <<= 1) {
            for (int j = 0; j < lim; j += (i << 1)) {
                for (int k = 0; k < i; k++) {
                    a[j + k + i] += a[j + k] * type;
                }
            }
        }
    }
    template<typename T>
    void and_fwt(vector<T>& a, int lim, int type) {
        a.resize(lim, 0);
        for (int i = 1; i < lim; i <<= 1) {
            for (int j = 0; j < lim; j += (i << 1)) {
                for (int k = 0; k < i; k++) {
                    a[j + k] += a[j + k + i] * type;
                }
            }
        }
    }
    template<typename T>
    void xor_fwt(vector<T>& a, int lim, int type) {
        a.resize(lim, 0);
        for (int i = 1; i < lim; i <<= 1) {
            for (int j = 0; j < lim; j += (i << 1)) {
                for (int k = 0; k < i; k++) {
                    T x = a[j + k], y = a[j + k + i];
                    a[j + k] = x + y;
                    a[j + k + i] = x - y;
                    if (type == -1) {
                        a[j + k] /= 2;
                        a[j + k + i] /= 2;
                    }
                }
            }
        }
    }

    template<typename T>
    vector<T> convo(vector<T> f, vector<T> g, string opt) {
        assert(opt == "or" || opt == "and" || opt == "xor");
        int n = SZ(f), m = SZ(g);
        int lim = 1 << (__lg(max(n, m)) + 1);
        if (opt == "or") {
            or_fwt(f, lim, 1);
            or_fwt(g, lim, 1);
        } else if (opt == "and") {
            and_fwt(f, lim, 1);
            and_fwt(g, lim, 1);
        } else {
            xor_fwt(f, lim, 1);
            xor_fwt(g, lim, 1);
        }
        vector<T> h(lim);
        for (int i = 0; i < lim; i++) {
            h[i] = f[i] * g[i];
        }
        if (opt == "or") {
            or_fwt(h, lim, -1);
        } else if (opt == "and") {
            and_fwt(h, lim, -1);
        } else {
            xor_fwt(h, lim, -1);
        }
        return h;
    }
}

文章操作

字符串部分

一. 字符串通用算法

Ⅰ. 字符串哈希

Ⅰ. kmp 算法

Ⅰ. manacher 算法（马拉车算法）

Ⅰ. AC 自动机

一. 树形数据结构

Ⅰ. 树状数组

Ⅰ. cdq 分治

Ⅰ. ST 表（求解区间 RMQ）

一. 最短路与最小生成树进阶

Ⅰ. 同余最短路

Ⅰ. tarjan 算法求强连通分量并缩点

Ⅰ. 无向图三元环计数

Ⅰ. Dinic 算法求最大流

Ⅰ. 树上启发式合并（Dsu on tree）

Ⅰ. 欧拉路的判定与求解

Ⅱ. 平面图的判定

数学部分

一. 数论基础

Ⅰ. 扩展欧几里得算法（exgcd）

定义

性质

证明

求原根的算法流程：

Ⅰ. 线性筛

反演过程

常用数论函数

常用结论

解决问题

解决方法

时间复杂度

Ⅰ. 线性基

Ⅰ. 拉格朗日插值

前置知识

结论推导

一个例题

Ⅰ. 组合数的基本性质

排列数与组合数

杨辉三角、组合数的一些恒等式、二项式定理

范德蒙德卷积

卡特兰数

概率生成函数 PGF

第六重——第二类斯特林数

1. 递推式

2. 通项式

3. 行的计算

4. 列的计算

5. 应用

六. 计算几何

Ⅰ. 向量基础运算

Ⅰ. 多项式求逆

相关推荐

评论