题解：P14528 [BYOI R1] 雨后屋檐

在模拟赛的时候用了一个自我感觉是紫的观察过了一道绿，不甘心。发现这题也可以用这个观察，而且这题是紫，于是就将其做掉，嘱以题解以记之。

思路

我们考虑把山画出图来：

蓝色的横线是水位线，不难发现积了水的部分可以被分成两类：

被填满了（即 $H\ge\min\{h_{L},h_{R}\}$ ）；
没被填满（即 $H<\min\{h_L,h_R\}$ ）。

显然，对于被填满了的部分，无论水位线是多少，内部积的水量是固定的。对于位置

i

来说，我们记其后第一个高度大于等于

h_i

的位置为

nxt_i

，则内部积的水量为：

h_i\times(nxt_i-i-1)-\sum_{k\in(i,nxt_i)}h_k

这是向后的部分，向前的部分也同样，我们把对应的积水量放到每一个位置上，这一部分可以通过两次单调栈求出。

我们把

i\to nxt_i

连一条边，则最终数列会呈现出森林的结构，于是被填满的水坑中的水我们就可以直接倍增跳树求出，时间复杂度单

\log

。

现在考虑没被填满的部分怎么求？

考虑把整个图旋转

90\degree

，我们可以得到：

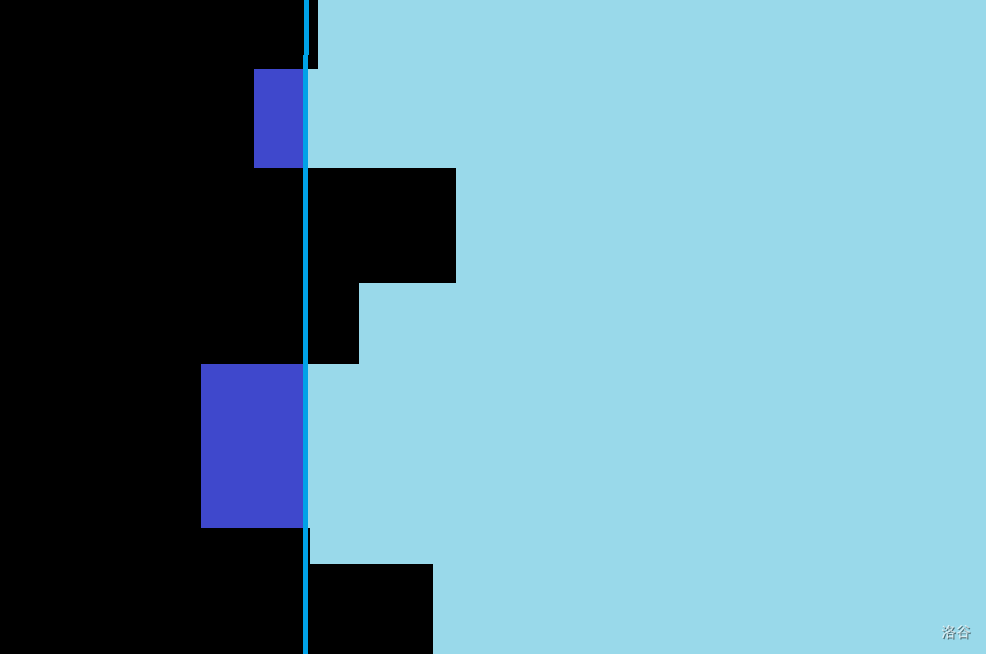
现在，把纵轴看成是时间轴，横轴看成是值域，蓝色部分打上 $1$ 的权值，则问题转化为了在某段时间中求值域上的一段前缀和。

这是什么？是可持久化线段树板子，时间复杂度单

\log

，于是你就美美的做完了这一题。

实现细节

值域很大，必须动态开点，所以空间必须开够。
由于下一次版本是更新的一段后缀（区间），所以在可持久化线段树上是不能进行 pushdown 的，否则就会改变两个版本共用部分的值，必须进行标记永久化。

代码

写了不到 3k，还是很好实现的。

代码

CPP

#include <iostream>
#include <cstdio>
#include <cassert>
#include <algorithm>
#define ll long long
#define mid ((l+r)>>1)
#define BUG cout<<"BUG\n";
using namespace std;
const ll N=5e5+10;
const ll V=1e9+2;
int lc[N*60],rc[N*60],tot,head[N];
ll sum[N*60],tag[N*60],h[N];
inline void push_up(int x,int l,int r){sum[x]=sum[lc[x]]+sum[rc[x]]+(ll)(l-mid+1)*tag[lc[x]]+(ll)(r-mid)*tag[rc[x]];}
void build(int &x,int lstx,int l,int r,int L,int R){
	if(!x) x=++tot;
	assert(tot<N*40);
	sum[x]=sum[lstx];
	tag[x]=tag[lstx];
	if(L<=l&&r<=R){
		tag[x]+=1;
		lc[x]=lc[lstx],rc[x]=rc[lstx];
		return;
	}
	if(L<=mid) build(lc[x],lc[lstx],l,mid,L,R);
	else lc[x]=lc[lstx];
	if(R>mid) build(rc[x],rc[lstx],mid+1,r,L,R);
	else rc[x]=rc[lstx];
	push_up(x,l,r);
}
ll query(int x,int l,int r,int L,int R,ll lazy){
	if(L<=l&&r<=R) return sum[x]+(ll)(r-l+1LL)*(lazy+tag[x]);
	ll ret=0;
	if(L<=mid) ret+=query(lc[x],l,mid,L,R,lazy+tag[x]);
	if(R>mid) ret+=query(rc[x],mid+1,r,L,R,lazy+tag[x]);
	return ret;
}
int nxt[N][20],stk[N],top,pre[N][20];
ll val_nxt[N],val_pre[N],presum[N];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	ll n,q,t;cin>>n>>q>>t;
	for(ll i=1;i<=n;i++){
		cin>>h[i];presum[i]=presum[i-1]+h[i];
		build(head[i],head[i-1],1,V,h[i]+1,V);
	}
	for(ll i=1;i<=n;i++){
		while(top&&h[i]>=h[stk[top]]){
			nxt[stk[top]][0]=i;
			val_nxt[stk[top]]=(ll)(i-stk[top]-1)*h[stk[top]];
			val_nxt[stk[top]]-=presum[i-1]-presum[stk[top]];
			top--;
		}
		stk[++top]=i;
	}
	for(ll i=n;i>=1;i--){
		for(ll j=1;j<20;j++) nxt[i][j]=nxt[nxt[i][j-1]][j-1];
		val_nxt[i]+=val_nxt[nxt[i][0]]; 
	}
	top=0;
	for(ll i=n;i>=1;i--){
		while(top&&h[i]>=h[stk[top]]){
			pre[stk[top]][0]=i;
			val_pre[stk[top]]=(ll)(stk[top]-i-1)*h[stk[top]];
			val_pre[stk[top]]-=presum[stk[top]-1]-presum[i];
			top--;
		}
		stk[++top]=i;
	}
	for(ll i=1;i<=n;i++){
		for(ll j=1;j<20;j++) pre[i][j]=pre[pre[i][j-1]][j-1];
		val_pre[i]+=val_pre[pre[i][0]];
	}
	ll lastans=0,ans=0;
	while(q--){
		ll lp,rp,Hp;
		cin>>lp>>rp>>Hp;
		lp^=t*lastans,rp^=t*lastans,Hp^=t*lastans;
		assert(lp<=rp&&lp<=n&&rp<=n&&lp>=1&&rp>=1&&Hp<=V);
		ll L=lp,R=rp;
		for(ll i=19;i>=0;i--){
			if(nxt[L][i]!=0&&nxt[L][i]<=rp&&h[nxt[L][i]]<Hp)
				L=nxt[L][i];
		}
		for(ll i=19;i>=0;i--){
			if(pre[R][i]!=0&&pre[R][i]>=lp&&h[pre[R][i]]<Hp&&pre[R][i]>=L)
				R=pre[R][i];
		}
		if(R==L){
			lastans=val_nxt[lp]-val_nxt[L]+val_pre[rp]-val_pre[R];
		}
		else{
			if(h[L]<Hp) L=nxt[L][0];
			if(h[R]<Hp) R=pre[R][0];
			lastans=val_nxt[lp]-val_nxt[L]+val_pre[rp]-val_pre[R];
			lastans+=query(head[R],1,V,1,Hp,0);
			lastans-=query(head[L-1],1,V,1,Hp,0);
		}
		ans^=lastans;
	}
	cout<<ans;
	return 0;
}

题解：P14528 [BYOI R1] 雨后屋檐

文章操作

思路

实现细节

代码

相关推荐

评论

题解：P14528 [BYOI R1] 雨后屋檐