题解：P3907 环的异或

我们可以将一个图

G=(V,E)

转化为它的一颗生成树

T=(V,E')

，那么图中的环必然是由两条树上的链与几条非树边构成的，如下图：

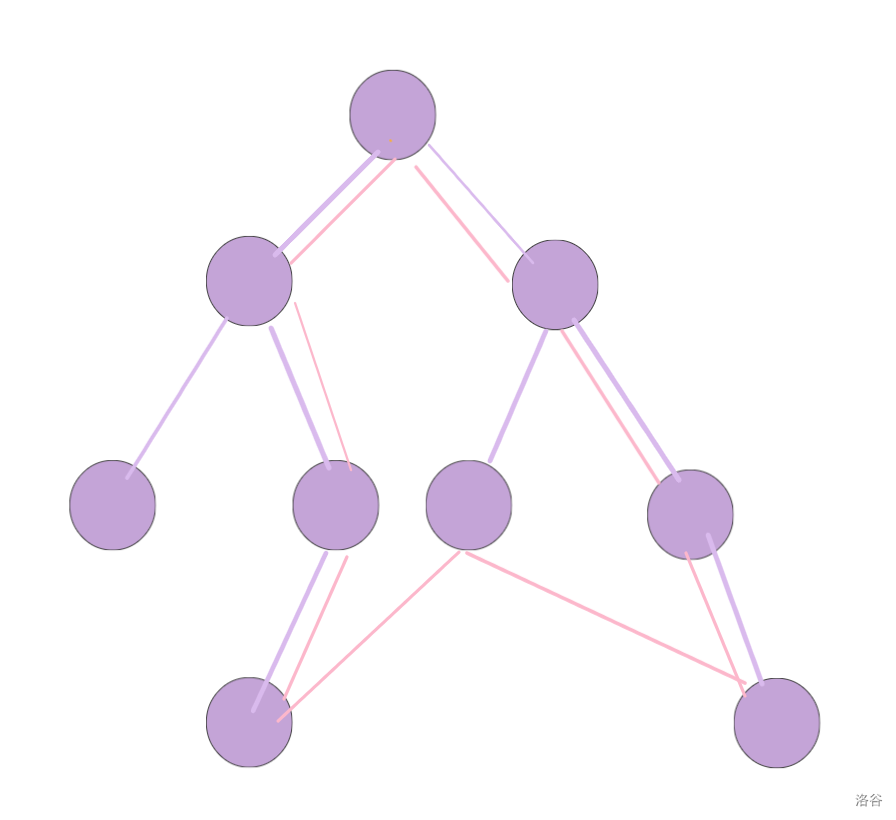
其中粉边即为一个环，但此时这个环是不好求的，因为它包括了两条非树边，对于这种有多条非树边的环，我们将其拆成多个单条非树边的环，如下图中的蓝环与红环：

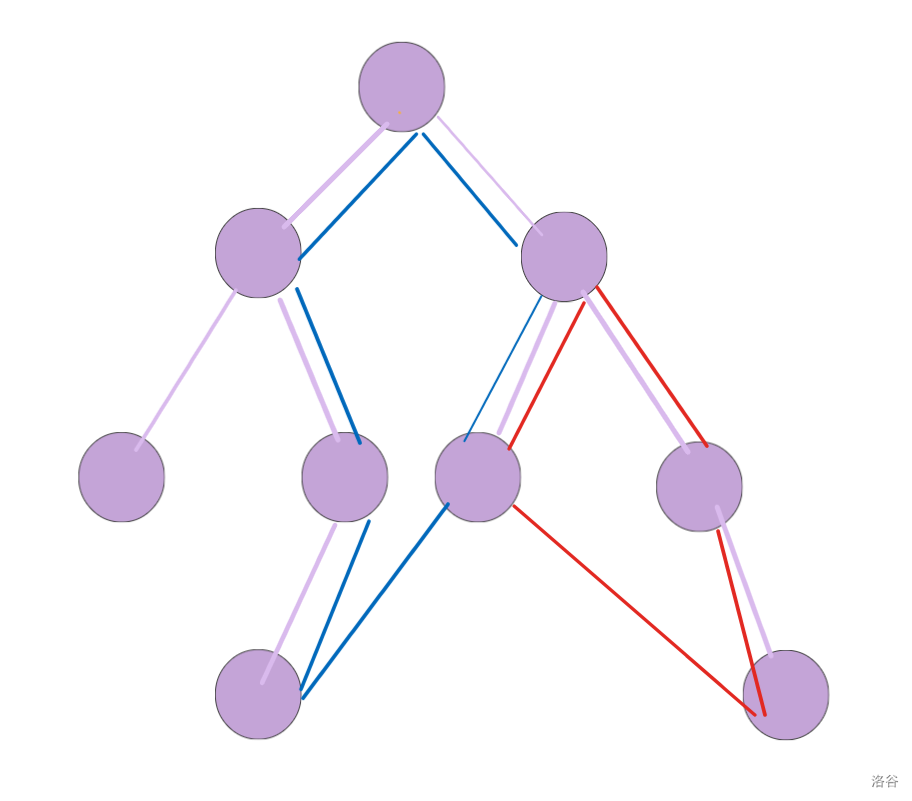
这样为什么是正确的呢？因为我们考虑的是环上边的异或值，我们将单环拆成多环相当于补上了部分重复边，而重复边又是经过偶数次的，所以异或一个值偶数次与不异或这个值是等效的，所以有多条非树边的环满足异或值等于 0 的充要条件即其拆出的多个单条非树边的环异或值等于 0，所以我们只需要计算每个非树边值异或左前缀路径异或值再异或右前缀路径异或值即可。这样我们只需要随意实现一个原图的生成树，再记录每个节点的前缀路径异或值，最后判断每个非树边即可，时间复杂度是

O(m\alpha(n))

的，瓶颈在于并查集实现生成树。

CODE

CPP

#include<bits/stdc++.h>
using namespace std;
int t,n,m;
vector<pair<int,int>> e[55];
int f[55],top;
struct node{
    int u,v,w;
}ed[55];
int sum[55],book[55];
int getf(int x){return (x==f[x])?x:f[x]=getf(f[x]);}
void dfs(int x,int fa){
    book[x]=1;
    for(auto i:e[x])if(i.first!=fa)sum[i.first]=i.second^sum[x],dfs(i.first,x);
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>t;
    while(t--){
        cin>>n>>m;
        top=0;
        for(int i=1;i<=n;i++)e[i].clear(),f[i]=i,book[i]=0;
        for(int i=1;i<=m;i++){
            int x,y,z;
            cin>>x>>y>>z;
            int fx=getf(x),fy=getf(y);
            if(fx!=fy)f[fx]=fy,e[x].push_back({y,z}),e[y].push_back({x,z});
            else ed[++top]={x,y,z};
        } 
        for(int i=1;i<=n;i++)if(!book[i])sum[i]=0,dfs(i,i);
        bool fl=true;
        for(int i=1;i<=top&&fl;i++)fl&=!(sum[ed[i].u]^sum[ed[i].v]^ed[i].w);
        cout<<((fl)?"Yes\n":"No\n");
    }
    return 0;
}

题解：P3907 环的异或

文章操作

CODE

相关推荐

评论

题解：P3907 环的异或