专栏文章
可持久化块状数组(分块可持久化)
算法·理论参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @min0h3vl
- 此快照首次捕获于
- 2025/12/01 18:33 3 个月前
- 此快照最后确认于
- 2025/12/01 18:33 3 个月前
省流:全是垃圾。
分块可持久化
可以有 的随机访问和 的修改。本做法可以通过 的数据点,得到 分。
例题
你需要维护这样的一个长度为 的数组,支持如下两种操作:
-
在某个历史版本上修改某一个位置上的值。
-
访问某个历史版本上的某一位置的值。
每次产生一个新的版本,2. 生成完全一样的版本。
共进行 次操作。
对于 的数据,。
对于 的数据:;
我们将这个长为为 的数组分为长为 的块(不能整除就空着):
如果我们要更改第 个元素,则新的版本长这样:
我们发现,只有第二个块改变了。也就是说,对于一个新的版本,仅有不超过 个被修改的块。我们可以这样表示新的版本:
ver 0: 1 2 3 | 4 5 6 | 7 8 9如果我们要更改第 个元素,则新的版本长这样:
ver 1: 1 2 3 | 4 5 0 | 7 8 9我们发现,只有第二个块改变了。也就是说,对于一个新的版本,仅有不超过 个被修改的块。我们可以这样表示新的版本:
ver 1: ----- | 4 5 0 | -----那么,对于每个版本,我们可以维护其 个块的指针;对于每个块,分配一块内存存储它的数据。
修改的时候,从修改的块复制建立新的块并修改元素;其余块复制指针。
查询的时候,直接读取返回。需要复制所有指针。
P1(1 2 3) P2(4 5 6) P3(7 8 9) V0(P1 P2 P3)修改的时候,从修改的块复制建立新的块并修改元素;其余块复制指针。
P4(4 5 0) V1(P1 P4 P3)查询的时候,直接读取返回。需要复制所有指针。
V3(P1 P4 P3)给一张数据不一样的图片。版本一是 ,二是 。
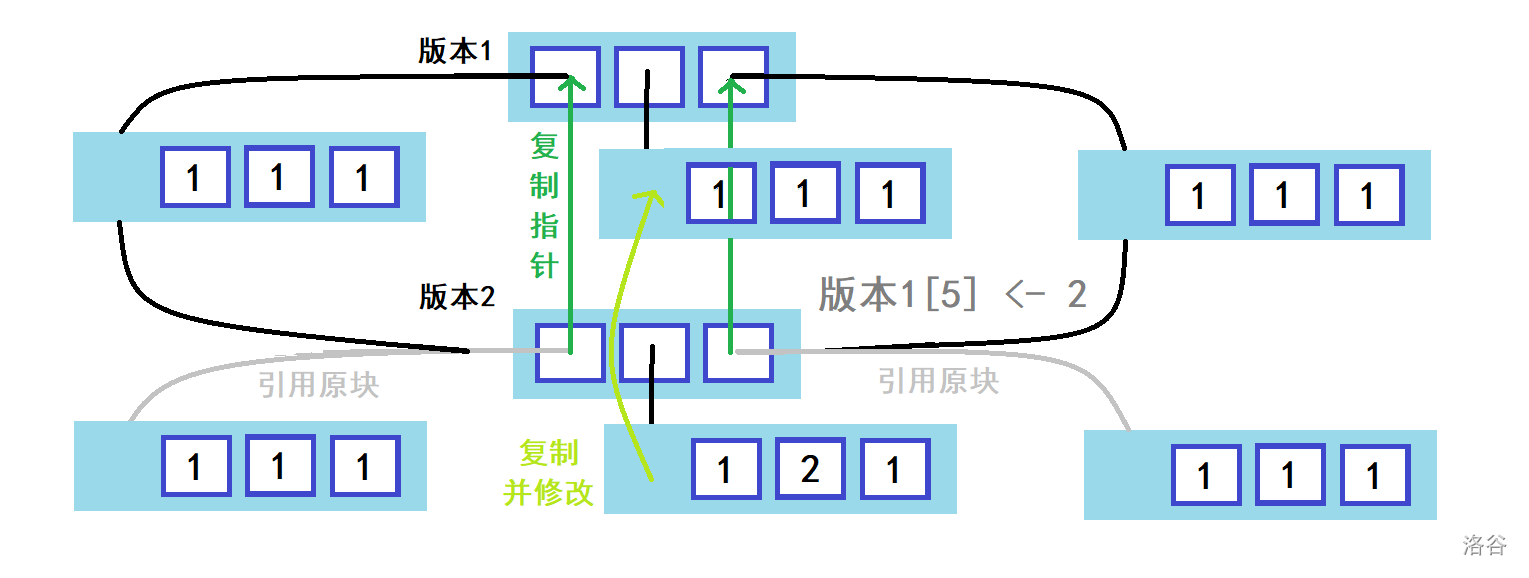
出于方便,接下来的代码中使用 开始的下标。第 个元素在第
在创建初始版本时,我们先算出块数,然后依次填充每个块。第 块的范围是 。
CPPi / B(即 )块,在块中的第 i % B(即 )个。在创建初始版本时,我们先算出块数,然后依次填充每个块。第 块的范围是 。
#define N 100900
#define B 350
int n, m, a[N];
array<array<int, 355>*, 355> v[N];
// v[i][j] 是版本 i 的第 j 块
// (*v[i][j])[k] 是它的第 k 个元素
void build() {
int cnt = n / B + 1;
up (i, 0, cnt - 1) {
v[0][i] = new array<int, 355>;
copy(a + i * B, a + (i + 1) * B, v[0][i]->begin());
}
}
当我们进行 修改 时,
- 从父版本复制所有的块的指针;
- 从需要修改的块复制新的块;
- 修改新块中需要修改的值。
我们可以求出每个元素的块号 和块内编号 。具体见代码。
CPP// 旧版本 新版本 位置 值
void update(int f, int g, int p, int k) {
int x = p / B, y = p % B;
v[g] = v[f];
v[g][x] = new array<int, 355>(*v[f][x]);
(*v[g][x])[y] = k;
}
当我们进行 查询 时,直接查就行(雾
记得复制。
CPP记得复制。
int query(int f, int g, int p) {
int x = p / B, y = p % B;
v[g] = v[f];
return (*v[g][x])[y];
}
最后是完整代码。
56分代码
CPP#include <bits/stdc++.h>
#define endl '\n'
#define up(i,l,r) for(int i=(l),E##i=(r);i<=E##i;++i)
#define dn(i,r,l) for(int i=(r),E##i=(l);i>=E##i;--i)
#define N 100900 // 对,只能拿 56 分
#define B 350
using namespace std;
int n, m, a[N];
array<array<int, 355>*, 355> v[N];
void build() {
int x = n / B + 1;
up (i, 0, x - 1) {
v[0][i] = new array<int, 355>;
copy(a + i * B, a + (i + 1) * B, v[0][i]->begin());
}
}
void update(int f, int g, int p, int k) {
int x = p / B, y = p % B; // x 是块号,y 是在块内的编号
v[g] = v[f];
v[g][x] = new array<int, 355>(*v[f][x]);
(*v[g][x])[y] = k;
}
int query(int f, int g, int p) {
int x = p / B, y = p % B;
v[g] = v[f];
return (*v[g][x])[y];
}
int main() {
int f, op, p, c;
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m;
up (i, 0, n - 1) cin >> a[i];
build();
up (i, 1, m) {
cin >> f >> op >> p;
--p;
if (op == 1) {
cin >> c;
update(f, i, p, c);
} else {
cout << query(f, i, p) << endl;
}
}
}
可以类似的写分块套分块,就只有 的复杂度了。常数太大可能要套
inf 层。懒得写。区间操作
很明显可以做。只有两个块被 部分 修改了,其余打标记,所以是 的。
注意不能在块里存标记,否则复杂度会炸掉。在版本信息里存标记的复杂度才是对的。
笼统地来说,如果只需要新建 个块,则都可以持久化。标记作为版本信息即可。
根号重构
本做法可以通过 的数据点,得到 分。
我们可以直接记录父版本和最后一次修改。顺便的,我们记录已经修改了几次,以及初始数组的指针。
CPP#define N 1000005
#define C 1000
struct Ver {
int *an;
int fa;
int p, c;
int cnt;
} b[N];
int a[N], v, op, p, c;
b[0] = {a, -1, 0, 0, 0}; // build
查询的时候从新到旧遍历所有修改,改过的去最新的值;否则取初始值。这样,修改的复杂度是 ,查询 ,空间复杂度均为 。
CPPint query(int x) {
b[x] = b[v];
for (int i = x; i != -1; i = b[i].fa) // 从新到旧
if (b[i].p == p)
return b[i].c;
return b[x].an[p];
}
void update_1(int x) {
b[x] = {b[v].an, v, p, c, b[v].cnt + 1};
}
复杂度瓶颈在于,如果修改了太多次,则查询会很耗时间。因此当
CPPcnt 大于一个定值 时,可以遍历历史修改进行一次重构。重构的复杂度是 ,均摊 ,查询 。可以取 。void update(int x) {
b[x] = {b[v].an, v, p, c, b[v].cnt + 1};
if (b[x].cnt < C) return;
// 重构
b[x].an = new int[n + 1];
up (i, 1, n) b[x].an[i] = b[v].an[i];
memset(ch, 0, sizeof ch);
for (int i = v; i != -1; i = b[i].fa)
if (!ch[b[i].p]) {
b[x].an[b[i].p] = b[i].c;
ch[b[i].p] = 1;
}
b[x].fa = -1, b[x].cnt = 1;
}
时间复杂度最差 。当然过不了。
84分代码
CPP#include <bits/stdc++.h>
#define endl '\n'
#define up(i,l,r) for(ll i=(l),E##i=(r);i<=E##i;++i)
#define dn(i,r,l) for(ll i=(r),E##i=(l);i>=E##i;--i)
using namespace std; typedef long long ll;
constexpr ll N = 5 + 1e6;
int n, m, v, op, p, c;
struct ver {
int *an, fa, p, c, cnt;
} b[N];
int a[N];
bool ch[N];
void update(int x) {
b[x] = {b[v].an, v, p, c, b[v].cnt + 1};
if (b[x].cnt < 1000) return;
b[x].an = new int[n + 1];
up (i, 1, n) b[x].an[i] = b[v].an[i];
memset(ch, 0, sizeof ch);
for (int i = v; i != -1; i = b[i].fa)
if (!ch[b[i].p]) {
b[x].an[b[i].p] = b[i].c;
ch[b[i].p] = 1;
}
b[x].fa = -1, b[x].cnt = 1;
}
int query(int x) {
b[x] = b[v];
for (int i = x; i != -1; i = b[i].fa)
if (b[i].p == p)
return b[i].c;
return b[x].an[p];
}
int main() {
cin >> n >> m;
up (i, 1, n) cin >> a[i];
b[0] = {a, -1, 0, 0, 1};
up (i, 1, m) {
cin >> v >> op >> p;
if (op == 1) {
cin >> c;
update(i);
} else {
cout<<query(i)<<endl;
}
}
return 0;
}
这就是常数水数据的力量。
区间操作
不好写,常数大,不建议使用。 另外主包不会区间查询。
水一点字数。区间加,单点求值为例:
首先原始数组需要分块,只读就行。其他依旧。
CPP#define N 100505 // 偷偷把数据范围改了 ^_^
#define B 350
struct ver {
int *a;
int fa;
int l, r, v;
int cnt;
} b[N];
int n, m, c, a[N], f, op, p, q, k, l[N], r[N], v[N];
b[0] = {a, p, -1, 0, 0, 0};
查询:读一下原始版本,从旧到新计算更改。
CPPvoid rec(int x) {
dn(i, b[x].cnt, 1) {
l[i] = b[x].l;
r[i] = b[x].r;
v[i] = b[x].v;
x = b[x].fa;
}
}
void query(int x) {
b[x] = b[fa];
rec(x);
int ret = b[x].an[p];
up (i, 1, b[x].cnt)
if (l[i] <= p && r[i] >= p)
ret += v[i];
return ret;
}
重构的时候,只需要一样记录所有历史修改,把区间端点提出来,排序去重离散化,建一个数组专门记录标记,对所有历史修改从旧到新,简简单单重构好了。没有参考代码。
CPPlower_bound 找到离散化位置,暴力挨个区间标记,复杂度 ,然后复制原数组,挨个区间进行修改(相当于 pushdown),就int t, cr[N], co[N];
void update(int x) {
b[x] = {b[f].a, f, p, q, k, b[f].cnt + 1};
if (b[x].cnt < B) return;
fill(co, co+B*3, 0);
rec(x);
up (i, 1, b[x].cnt)
cr[t++] = l[i], cr[t++] = r[i] + 1;
sort(cr, cr+t);
t = unique(cr, cr+t) - cr - 1;
up (i, 1, b[x].cnt) {
int lc = lower_bound(cr, cr+t, l[i]) - cr;
int rc = lower_bound(cr, cr+t, r[i]+1) - cr;
up (j, lc, rc - 1) co[i] += v[i];
}
b[x].a = new int[n];
up (i, 0, t - 2) {
up (j, cr[i], cr[i + 1] - 1)
b[x].a[j] = b[f].a[j] * co[i];
}
}
真没必要用了。
可持久化块状链表
参考代码(未测试)
CPP#include <bits/stdc++.h>
#define fo(i,l,r) for(ll i=(l),E##i=(r);i<=E##i;++i)
#define of(i,r,l) for(ll i=(r),E##i=(l);i>=E##i;--i)
using namespace std; typedef long long ll;
constexpr int N = 100005, B = 350, C = 355;
vector<int> e[N * 4];
int cnt = 0;
struct ver {
int c; // block count
int p; // prefix sum of length
int b; // blocks
};
int get(ver v, int p) {
auto& vp = e[v.p], vb = e[v.b];
int bl = lower_bound(vp.begin(), vp.end(), p) - vp.begin();
return e[vb[bl]][p - vp[bl]];
}
#define FCC \
ver u = v; \
auto& ub = e[u.b = cnt]; e[cnt++] = e[v.b]; \
auto& vp = e[v.p], vb = e[v.b]; \
int bl = lower_bound(vp.begin(), vp.end(), p) - vp.begin(); \
auto& be = e[ub[bl] = cnt]; e[cnt++] = e[vb[bl]];
ver set(ver v, int p, int x) {
FCC;
be[p - vp[bl]] = x;
return u;
}
ver ins(ver v, int p, int x) {
FCC;
auto& up = e[u.p = cnt]; e[cnt++] = e[v.p];
be.insert(be.begin() + (p - vp[bl]), x);
fo (i, bl + 1, u.c - 1) ++up[i];
if (be.size() > B << 1) {
++u.c;
ub.insert(ub.begin() + (bl + 1), cnt);
up.insert(up.begin() + (bl + 1), up[bl] + B);
e[++cnt] = vector<int>(be.begin() + B, be.end());
be.erase(be.begin() + B, be.end());
}
return u;
}
ver del(ver v, int p) {
FCC;
auto& up = e[u.p = cnt]; e[cnt++] = e[v.p];
be.erase(be.begin() + (p - vp[bl]));
fo (i, bl + 1, u.c - 1) --up[i];
if (be.size() < B >> 1 && bl != u.c - 1) {
--u.c;
be.insert(be.end(), e[ub[bl + 1]].begin(), e[ub[bl + 1]].end());
ub.erase(ub.begin() + (bl + 1));
up.erase(up.begin() + (bl + 1));
}
return u;
}
后记
唯一的作用就是好写。至于更多的用处,建议问 noip。
AI 使用说明:作者使用 DeepSeek 辅助了调试。
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...