专栏文章

题解：P3373 【模板】线段树 2

__droplet_
P3373题解参与者 3已保存评论 3

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
3 条
当前快照
1 份
快照标识符
@miprsg1u
此快照首次捕获于
2025/12/03 16:53
3 个月前
此快照最后确认于
2025/12/03 16:53
3 个月前
查看原文
本题解使用 动态开点线段树。

方法

暴力时间复杂度 O(n2)O(n^2)，肯定挂，考虑线段树。

复习线段树

线段树，将每一个区间分成个两个长度为 len2\frac{len}{2} 的区间，下图是一棵长度 nn 为 44 的线段树，每个点维护一个值 valval。

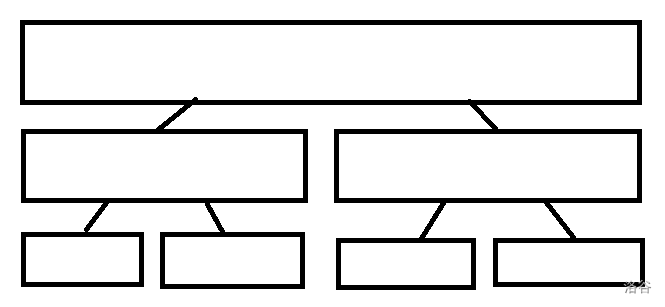
建树

对于每个线段 xx，先建自己的子树，到最后一层时初始化 valval，接下来更新上方的 valval。

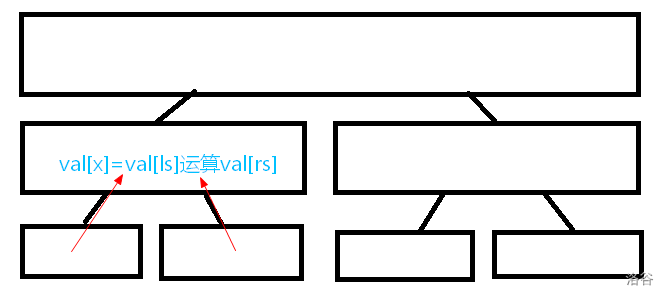
修改

考虑对每个区间修改，发现时间复杂度 O(nlog⁡n)O(n\log{n})，比暴力还差。
考虑当这个修改覆盖这一整个区间时，使用懒标记 tagtag 记录，当下次修改或查询时将懒标记下传给左右子数，别忘了更新上方的 valval。

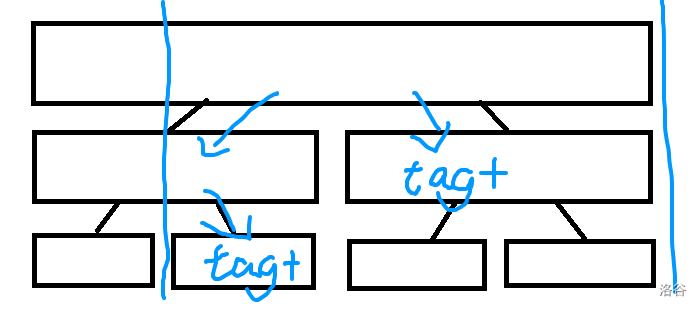
查询

几乎与修改一样，这个查询覆盖这一整个区间时，直接返回 valval，当下次修改或查询时将懒标记下传给左右子数。

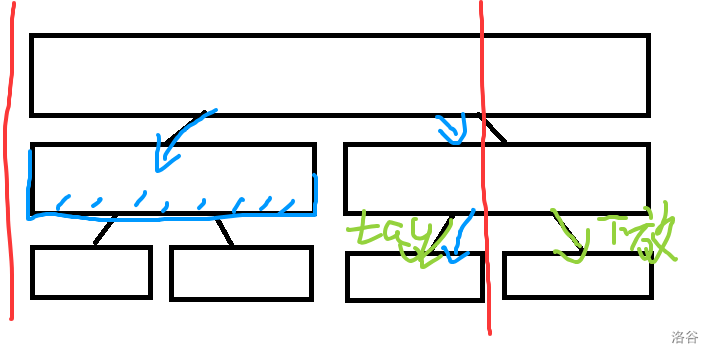
本题题解

考虑将 tagtag 分成两个，加法标记 addadd 和乘法标记 mulmul。其余同上。

注意事项

在下放 addadd 标记时受 mulmul 标记影响，更新 valval 时先乘后加。
mulmul 初始化为 11。
在乘法时也要更新 addadd 标记，相当于 addadd 也变成了多倍。

代码

CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=400010;
int n,q,m,a[N],rt,tc;
int ls[N],rs[N],val[N],add[N],mul[N];

void pushup(int x){ // 更新val，上传
	val[x]=(val[ls[x]]+val[rs[x]])%m;
}

void pushdown(int x,int l,int r){ // 更新 tag，下放（l,r 为区间左右端点）
	int mid=(l+r)>>1;
	val[ls[x]]=(val[ls[x]]*mul[x]+add[x]*(mid-l+1))%m; // 先乘后加
	val[rs[x]]=(val[rs[x]]*mul[x]+add[x]*(r-mid))%m;
	mul[ls[x]]=(mul[ls[x]]*mul[x])%m;
	mul[rs[x]]=(mul[rs[x]]*mul[x])%m;
	add[ls[x]]=(add[ls[x]]*mul[x]+add[x])%m; // add 更新受 mul 影响
	add[rs[x]]=(add[rs[x]]*mul[x]+add[x])%m;
	mul[x]=1;
	add[x]=0;
}

void build(int &x,int l,int r){ // 建树（l,r 为区间左右端点）
	x=++tc;
	add[x]=0;mul[x]=1; // 乘法初始化为 1
	if(l==r){
		val[x]=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(ls[x],l,mid);
	build(rs[x],mid+1,r);
	pushup(x);
}

void update1(int x,int l,int r,int ql,int qr,int v){ // 乘法更新（l,r 为区间左右端点，ql,qr 为查询左右端点）
	if(ql<=l&&r<=qr){ // 整个区间在更新范围内，打 tag
		val[x]=(val[x]*v)%m;
		mul[x]=(mul[x]*v)%m;
		add[x]=(add[x]*v)%m; // add 标记也会被乘法更新
		return;
	}
	pushdown(x,l,r);
	int mid=(l+r)>>1;
	if(ql<=mid) update1(ls[x],l,mid,ql,qr,v);  // 若左子区间在更新范围内，更新
	if(mid<qr) update1(rs[x],mid+1,r,ql,qr,v); // 同上
	pushup(x);
}

void update2(int x,int l,int r,int ql,int qr,int v){ // 加法更新（l,r 为区间左右端点，ql,qr 为查询左右端点）
	if(ql<=l&&r<=qr){
		val[x]=(val[x]+v*(r-l+1))%m;
		add[x]=(add[x]+v)%m;
		return;
	}
	pushdown(x,l,r);
	int mid=(l+r)>>1;
	if(ql<=mid) update2(ls[x],l,mid,ql,qr,v);
	if(mid<qr) update2(rs[x],mid+1,r,ql,qr,v);
	pushup(x);
}

int query(int x,int l,int r,int ql,int qr){ // 查询（l,r 为区间左右端点，ql,qr 为查询左右端点）
	if(ql<=l&&r<=qr) return val[x];
	pushdown(x,l,r);
	int mid=(l+r)>>1,ans=0;
	if(ql<=mid) ans=(ans+query(ls[x],l,mid,ql,qr))%m;
	if(mid<qr) ans=(ans+query(rs[x],mid+1,r,ql,qr))%m;
	return ans;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>q>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	build(rt,1,n);
	while(q--){
		int op,x,y,k;
		cin>>op>>x>>y;
		if(op==1){
			cin>>k;
			update1(rt,1,n,x,y,k);
		}else if(op==2){
			cin>>k;
			update2(rt,1,n,x,y,k);
		}else{
			cout<<query(rt,1,n,x,y)<<"\n";
		}
	}
	return 0;
}

评论

共 3 条评论，欢迎与作者交流。

正在加载评论...