专栏文章

题解：P5410 【模板】扩展 KMP/exKMP（Z 函数）

yyueyan_WZF
P5410题解参与者 1已保存评论 0

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
0 条
当前快照
1 份
快照标识符
@mioi8h2r
此快照首次捕获于
2025/12/02 19:38
3 个月前
此快照最后确认于
2025/12/02 19:38
3 个月前
查看原文
太菜了，今天才刚学会。
题目链接。

Z 函数 定义

对于一个长度为 nn 的字符串 ss，定义函数 z[i]z[i] 表示 ss 和 s[i,n−1]s[i,n-1]（即以 s[i]s[i] 开头的后缀）的最长公共前缀 (LCP) 的长度，则 zz 被称为 ss 的 Z 函数。 ——OI Wiki

Solution

Part 1 暴力碾标算

考虑暴力，很容易可以想道 O(n2)O(n^2) 的做法：
CPP
z[1]=strlen(s+1);
for(int i=2;i<=strlen(s+1);i++){
	for(int j=1,k=i;k<=strlen(s+1);k++,j++){
		if(s[j]!=s[k]){	
			z[i]=j-1;
			break;
		}
		z[i]=j; 
	}
}
只能拿到 2929 分。

Part 2 正解

考虑跟 Manacher 一样的思路：
（S1S_1 表示原字符串 ss，SiS_i 表示以第 ii 个字符为开头的 SS 后缀，SmaxS_{max} 表示与 SS 的 LCP 最长的后缀）。
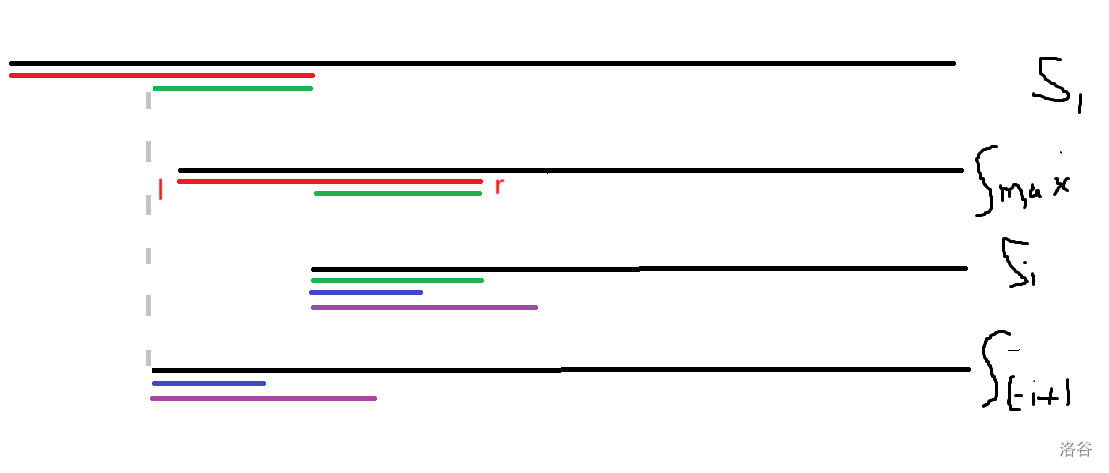
我们规定红色线段为 SS 后缀中 LCPLCP 的右端点目前最远的 LCPLCP。
那么 rr 表示右端点，ll 表示左端点。
再解释一下。
设以红色线段为 LCPLCP 的后缀为 SmaxS_{max}，以第 jj 个节点为开头的后缀为 SjS_j，一个后缀 ss 的 LCPLCP 右端点为 RsR_{s} 左端点为 LsL_{s}，则：
RSmax=max⁡ji−1RSjR_{S_{max}} = \max_{j }^{i-1} R_{S_j}
r=RSmax,l=LSmaxr=R_{S_{max}},l=L_{S_{max}}
那么我们这的绿色线段表示以 ii 为左端点，rr 为右端点的 SS 子串。
可以发现 SS 会有一段相对应的绿色线段，由于与 SmaxS_{max} 相对应，所以左端点为 l−i+1l-i+1。
那么就肯定会有一个后缀 Sl−i+1S_{l-i+1} 使得前缀为绿色线段，那么 SiS_i 的 Z 函数就可已从 Sl−i+1S_{l-i+1} 来转移，因为 Sl−i+1S_{l-i+1} 与 SiS_i 都是绿色前缀。
类似 Manacher 算法，我们分为两种情况：
  1. Zl−i+1Z_{l-i+1} 小于等于 rr 那么我们可以直接继承过来（即上图蓝色段）。
  2. Zl−i+1Z_{l-i+1} 大于 rr 那么我们只能取 ii 到 rr 的这段，因为外面段我们不能保证相同（即上图紫色段）。
继承后，我们再暴力一下，得到准确的答案。
最后还需要更新下 rr 与 ll。

Code

CPP
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e7+10;
char a[N],b[N];
int ans;
int z[N];
int p[N];
signed main(){
	ios::sync_with_stdio(false);
	cin>>(a+1)>>(b+1);
	int l=0,r=0;
	z[1]=strlen(b+1);
	for(int i=2;i<=strlen(b+1);i++){
		if(i<r) z[i]=min(z[i-l+1],r-i+1);
		while(i+z[i]<=strlen(b+1)&&b[i+z[i]]==b[z[i]+1]) {
			z[i]++;
		}
		if(r<i+z[i]-1){
			r=i+z[i]-1;
			l=i;
		}
	}
	for(int i=1;i<=strlen(b+1);i++){
		ans=ans^(i*(z[i]+1));
	}
	cout<<ans<<endl;
	l=0,r=0;
	for(int i=1;i<=strlen(a+1);i++){
		if(i<r) p[i]=min(z[i-l+1],r-i+1);
		while(i+p[i]<=strlen(a+1)&&a[i+p[i]]==b[p[i]+1]) {
			p[i]++;
		}
		if(r<i+p[i]-1){
			r=i+p[i]-1;
			l=i;
		}
	}
	ans=0;
	for(int i=1;i<=strlen(a+1);i++){
		ans^=(i*(p[i]+1));
	}
	cout<<ans;
}

评论

共 0 条评论，欢迎与作者交流。

正在加载评论...