专栏文章
题解:P3379 【模板】最近公共祖先(LCA)
P3379题解参与者 21已保存评论 25
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 25 条
- 当前快照
- 1 份
- 快照标识符
- @miptocwc
- 此快照首次捕获于
- 2025/12/03 17:46 3 个月前
- 此快照最后确认于
- 2025/12/03 17:46 3 个月前
Tarjan LCA
前言
Tarjan 老爷爷太聪明了,他不仅开发出来了求解图的连通性问题的算法,还开发出了求解 LCA 的算法。
Tarjan LCA 利用了并查集,可以在线性时间内离线求解。
其过程是记录下来所有询问,进行搜索,将搜索完的点记录到 数组,并向自己的父亲合并,在一个点 的子树处理完毕后处理所有和 点有关的询问,若另外一个点也已经访问过,则答案为另外一个点的并查集所指向的节点。
前置知识
- DFS。
- 并查集。
- 对于本篇题解,你还需要会使用 vector。
结合图片分析
口述难以理解,我们结合图片分析。假定我们要查询 和 的 LCA。
约定
find(x) 为并查集的搜索函数;merge(x,y) 为并查集的合并函数,其意义为将 合并到 。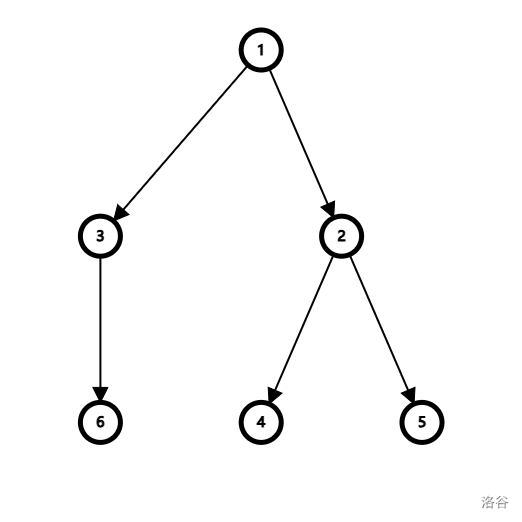
- 搜索到节点 ,设 为 true。
- 搜索到节点 ,设 为 true。
- 搜索到节点 ,设 为 true。没有儿子,
merge(6,3)。发现需要查询 和 的 LCA,但是此时 为 false,所以不进行操作。 - 回溯到 ,没有其他儿子,
merge(3,1)。 - 回溯到 ,搜索到节点 ,设 为 true。
- 搜索到节点 ,设 为 true。没有儿子,
merge(4,2),发现需要查询 和 的 LCA,此时 为 true,将两者答案设置为find(6),即 。
这样子,一次求解就完成了。
复杂度
对于大小为 的图进行遍历,进行 次询问,由于是离线查询,一次就可以完成,故时间复杂度为 。
代码实现
古希腊掌管 vector 的神。
CPP#include<bits/stdc++.h>
using namespace std;
const int MN=5e5+10;
int fa[MN],vis[MN],ans[MN],n,m,s;
vector<int> v[MN];
vector<pair<int,int>> ask[MN];
int find(int x){
if(fa[x]!=x) fa[x]=find(fa[x]);
return fa[x];
}
void merge(int x,int y){
x=find(x);
y=find(y);
fa[x]=y;
}
void tarjan(int x){
vis[x]=true;
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(vis[y]) continue;//无向图 防止遍历自己爹
tarjan(y);
merge(y,x);
}
for(int i=0;i<ask[x].size();i++){
int y=ask[x][i].first;
int id=ask[x][i].second;
if(vis[y]) ans[id]=find(y);
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for(int i=1;i<MN;i++) fa[i]=i;//初始化并查集
cin>>n>>m>>s;
for(int i=1;i<n;i++){
int x,y;
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
if(a==b) ans[i]=a;
else{
ask[a].push_back({b,i});
ask[b].push_back({a,i});
}
}
tarjan(s);
for(int i=1;i<=m;i++){
cout<<ans[i]<<"\n";
}
return 0;
}
相关推荐
评论
共 25 条评论,欢迎与作者交流。
正在加载评论...