笔者默认你已经会最短路算法了，这里就不讲解算法具体流程了。

~~（毕竟不会最短路也不会来看本文吧）~~

板子

Dijkstra：

CPP

struct node{
    int p,w;
    bool operator < (const node &x) const{
        return w > x.w;
    }
};
priority_queue<node> q;
int dis[100004];
bool f[100004];
inline void dij(int s) {
    q.push({s,0});
    memset(dis,0x3f,sizeof(dis));
    dis[s] = 0;
    while(!q.empty()) {
        node t = q.top();
        q.pop();
        if (f[t.p]) continue;
        f[t.p] = true;
        for (int i = head[t.p];i;i = e[i].nxt) {
            int v = e[i].to;
            if (dis[v]>dis[t.p]+e[i].w) {
                dis[v]=dis[t.p]+e[i].w;
                q.push({v,dis[v]});
            }
        }
    }
}

SPFA:

CPP

queue<int> q;
int dis[10004];
bool vis[10004];
void spfa(int x) {
    for (int i = 1; i <= n; i++) dis[i] = 0x7fffffff;
    dis[x] = 0;
    vis[x] = true;
    q.push(x);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        vis[t] = false;
        for (int i = head[t];i;i = e[i].nxt) {
            if (dis[e[i].to] > dis[t] + e[i].w) {
                dis[e[i].to] = dis[t] + e[i].w;
                if (vis[e[i].to]) continue;
                vis[e[i].to] = true;
                q.push(e[i].to);
            }
        }
    }
}

Floyd:

CPP

for (int k = 1; k <= n; k++) {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);
        }
    }
}

严格次短路： [USACO06NOV] Roadblocks G 多记一个次短的做就行了。

分层图最短路

有时候题目中对某些边会产生一些限制条件，比如可以免费经过一条边、某条边经过次数有限等等，共同特点是可以通过建模把各种合法状态都描述出来，这时候就可以考虑分层图最短路求解。

例题：（按难度主观升序排序）

[ABC395E] Flip Edge 板子。考虑全图实际上只存在两种状态：原图和反图。而两种状态切换需要 $X$ 的代价，所以建图即可。
[JLOI2011] 飞行路线 $k$ 很小，所以我们可以建出 $k+1$ 层图，层与层之间可以通过一条边权 $0$ 的单向边切换，然后对每一层的终点进行统计即可。
[BJWC2012] 冻结和上面很像，相信你自己可以想出来。
[NOI2025] 机器人认真读题，注意建模需要精细实现，不能直接显式建出所有点，考虑哪些点是没用的。通过工单 hack 数据后证明你的实现没有问题。
[CSP-J 2019] 加工零件其实好像并不是分层图，不过还是加上了。本人题解。
[CSP-J 2023] 旅游巴士模意义下分层图也是常见的 trick，想到这一点基本也就快做完了，这里就不写具体转移了，留作读者思考。
[USACO21JAN] Telephone G 好题一道，非常有意思。

P7297 [USACO21JAN] Telephone G

思路新奇的分层图最短路。

首先如果我们对品种开桶，然后把两种品种里的所有点两两连边，那么直接

O(n^2)

打飞。

发现

k

很小，只有

50

，考虑转化限制。

我们建立

k+1

层图，其中

1\sim k

层表示品种，每层的相邻两点之间连一条边权为

1

的双向边。第

k+1

层点之间不要连任何边，这一层的点的最短路数据才是从

1

传信息到这个点的最小花费。

然后最妙的就来了：

我们记

a_i

表示

i

的品种，从

a_i

层的

i

向

k+1

层的

i

连边权为

0

的单向边。然后记

a_i

能够交谈的品种有

b_j

，那么从

k+1

层的

i

向

b_j

层的

i

连一条边权为

0

的单向边。

这样有什么用呢？假如我们现在有点

1

品种为

1

，点

2

品种为

2

，点

3

品种为

3

，仅有品种

1

能向

3

传话。那么这个

1\to3

的更新过程就是从

k+1

层的

1

到

3

层的

1

，然后到

3

层的

2

，由于这一层的

2

没有向

k+1

层连边所以略过。再走到

3

层的

3

，再走向

k+1

层的

3

，更新答案。而其他的非法路径我们都不会去尝试。

利用分层图我们把信息传递的限制简洁地描述了出来，从而优化了复杂度。

样例图解：

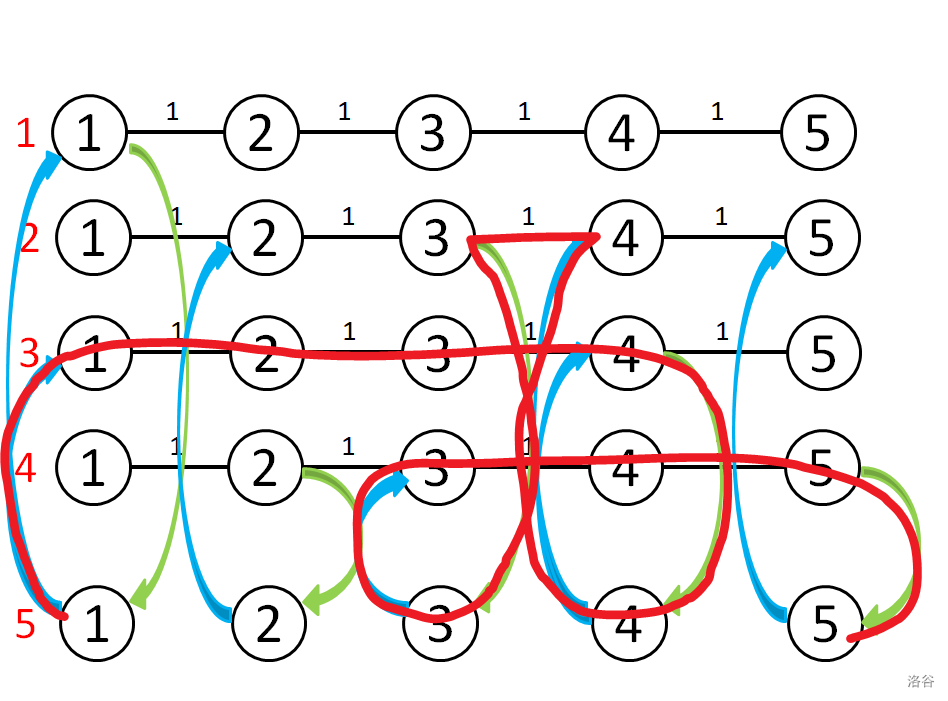
注意边权只有

0,1

，使用双端队列 bfs 比 dij 更快。

CPP

#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e6+10;
int n,k;
int b[maxn];
struct edge{
    int v,w;
};
vector<edge> e[maxn];
vector<int> c[maxn];
int dis[maxn];
deque<int> q;
inline void bfs(int s) {
    memset(dis,0x3f,sizeof(dis));
    dis[s] = 0;
    q.push_front(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop_front();
        for (auto i : e[u]) {
            int v = i.v,w = i.w;
            if (dis[v] != 0x3f3f3f3f) continue;
            if (w == 0) {
                dis[v] = dis[u];
                q.push_front(v);
            }else if(w == 1) {
                dis[v] = dis[u]+1;
                q.push_back(v);
            }
        }
    }
    if (dis[k*n+n] != 0x3f3f3f3f) cout << dis[k*n+n] << '\n';
    else cout << -1 << '\n';
}
int main() {
#ifdef LOCAL
    freopen("D:/codes/exe/a.in","r",stdin);
    freopen("D:/codes/exe/a.out","w",stdout);
#endif
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> b[i];
        e[(b[i]-1)*n+i].push_back({k*n+i,0});
        c[b[i]].push_back(i);
    }
    for (int i = 1; i <= k; i++) {
        for (int j = 1; j <= k; j++) {
            char x;
            cin >> x;
            if (x == '1') {
                for (auto v : c[i]) {
                    e[k*n+v].push_back({(j-1)*n+v,0});
                }
            }
        }
    }
    for (int i = 0; i < k; i++) {
        for (int j = 1; j < n; j++) {
            e[i*n+j].push_back({i*n+j+1,1});
            e[i*n+j+1].push_back({i*n+j,1});
        }
    }
    bfs(k*n+1);
    return 0;
}

差分约束

对于

n

元一次不等式，其每个式子的一般形式都形如：

a_x-a_y\le b

状物，简单转化形式之后即可以变为

a_x\le a_y+b

，和最短路最终形式的

dis_u+w\ge dis_v

很像，所以我们仿照最短路连边，建立超级源点跑 SPFA 后得到的值即为一组解，如果有负环则无解。

如果要求最终解最小需要跑最长路，反之亦然。

上述结论的证明

最小最大其实等价，我们这里考虑最短路为什么是最大解。

考虑所有式子形如：

dis_1+w_1\ge dis_2\\ dis_2+w_2\ge dis_3\\ dis_3+w_3\ge dis_4\\ \vdots\\ dis_{n-1}+w_w\ge dis_n

将上式求和可得

dis_1+W\ge dis_n

。

W

即为

1\to n

的任一路径。

我们现在需要最大化

a_n

，考虑

a_1+W

最小值为多少，显然就是

1\to n

的最短路。

所以我们得到的

dis_n

就是

a_n

的最大值。

见到一些二元不等关系可以向差分约束考虑。

例题：

小 K 的农场板子。
工程规划板子。
[HNOI2005] 狡猾的商人板子。
[USACO05DEC] Layout G 其实还是板子，不过需要注意 SPFA 的起点问题。判断有无解需要建超级源点，但是求 $dis_n-dis_1$ 最大值依旧需要从 $1$ 开始跑最长路。
[SCOI2011] 糖果需要动脑子的差分约束。

[SCOI2011] 糖果

等于号可以看成双向

0

边，大于小于号可以通过加减

1

变成大于等于小于等于号，跑 SPFA 最长路即可，然而数据范围不允许我们跑 SPFA。

但是发现

1,3,5

条件的边是可以缩点的，因为有等号所以一个强连通分量的点值一定相等，所以缩点后缩连

2,4

条件的边，如果还是一个 DAG 说明有解，topo dp 求最长路即可。否则出现环，那我们在环上反复刷可以无限增大最长路，所以无解。

[1007] 倍杀测量者相当综合的题目。

[1007] 倍杀测量者

不好想。

原题大概就是给你一系列不等式形如：

\begin{aligned} x_a\ge x_b(k_a-T)\\ x_a(k_a+T)\ge x_b \end{aligned}

给定

x_i,k_i

，求出最大的

T

使得不等式组无解。

第一步转化就不很好想，不等式组可以考虑差分约束，但乘法是没办法用最短路刻画的，不过上面只有简单的乘法，乘法可以转化为加法么？

可以的，我们取对数即可，上述两个式子即形如：

\begin{aligned} \log x_a\ge \log x_b+\log (k_a-T)\\ \log x_a+\log (k_a+T)\ge \log x_b \end{aligned}

这下子就是我们常见的形式了，可以建模。然后我们考虑怎么求最小的

T

。发现

T

有单调性，假如有

x

使得当前无解，则

\le x

的也一定无解，所以直接二分

T

，然后建图跑 SPFA 判有没有负环即可。

CPP

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3+20;
const double eps = 1e-6;
int n,s,t;
inline void read(int &x) {
    x=0;int f=1;char ch=getchar();
    while (ch<'0'||ch>'9') {
        if (ch=='-') f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9') {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    x*=f;
}
struct edge{
    int to;double w;int op;
};
vector<edge> e[maxn];
double dis[maxn];bool f[maxn];int cnt[maxn];
queue<int> q;
inline bool spfa(double t) {
    for (int i = 0; i <= n; ++i) dis[i] = -2e9,f[i] = false,cnt[i] = 0;
    q={};
    f[0] = true,dis[0] = 0;
    q.push(0);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        f[u] = false;
        for (auto i : e[u]) {
            int v = i.to;
            double w = i.w;
            if (i.op == 1) {
                w = log2(w-t);
            }else if (i.op == 2) {
                w = -log2(w+t);
            }
            if (dis[v] < dis[u] + w) {
                dis[v] = dis[u] + w;
                cnt[v] = cnt[u] + 1;
                if (cnt[v] > n) return true;
                if (!f[u]) {
                    q.push(v);
                    f[v] = true;
                }
            }
        }
    }
    return false;
}
int main() {
#ifdef LOCAL
    freopen("E:/codes/exe/a.in","r",stdin);
    freopen("E:/codes/exe/a.out","w",stdout);
#endif
    read(n),read(s),read(t);
    for (int i = 1; i <= n; i++) e[0].push_back({i,0,3});
    double l = 0,r = 2e9;
    for (int i = 1; i <= s; i++) {
        int o,a,b,k;
        read(o),read(a),read(b),read(k);
        if (o == 1) r = min((double)k,r);
        e[b].push_back({a,(double)k,o});
    }
    for (int i = 1; i <= t; i++) {
        int x,y;
        read(x),read(y);
        e[0].push_back({x,log2(y),3});
        e[x].push_back({0,-log2(y),3});
    }
    if (!spfa(0)) {
        puts("-1");return 0;
    }
    while (r-l >= eps) {
        double mid = (l + r) / 2;
        if (spfa(mid)) {
            l = mid;
        }else{
            r = mid;
        }
    }
    printf("%.10f",l);
    return 0;
}

Floyd

Floyd 求全源最短路本质上是一种 dp，通过枚举中转点来更新任意两点间的关系，所以利用这一点我们可以做很多事，动态维护加点全源最短路、连通性（传递闭包）等等。

例题：

道路重建
灾后重建以上两题都是板子，都应用了 floyd 的 dp 本质，所以我们可以动态的更新两点最短路（连通性）等等。
[USACO08JAN] Cow Contest S 二元关系常见的思路是图论建模，这个二元关系是有传递性的，所以我们可以通过 floyd 来进行维护。
[KOI 2025 #2] 通行费为了把 $1$ 变成 $0$ ，倒序跑 floyd 即可， $O(n^2m)$ 容易做到。仔细研究后可以发现，我们实际上是在用 $0$ 边合并连通块，一旦添加 $n-1$ 条有效的 $0$ 边则所有点两两之间最短路都为 $0$ （此时有效的 $0$ 边是全图的生成树），所以此时就不用再跑了，复杂度 $O(n^3)$ 。
[NOIP 2016 提高组] 换教室这题不给思路了，因为还涉及期望概率知识，比较综合的题目留给大家思考。
最小密度路径破坏最短路性质的除法很讨厌，我们不妨把它记到状态里从而保留最短路性质。

这样 $f_{i,j,k}=\min(f_{i,p,cnt}+f_{p,j,k-cnt},f_{i,j,k})$ ，但这个式子暴力做是 $O(n^5)$ 的，过不了。

不过我们认真思考可以发现，我们不需要枚举 $cnt$ ，因为这个决策会被 $f_{i,j,k}=\min(f_{i,pre_j,k-1}+f_{pre_j,j,1},f_{i,j,k})$ 覆盖（ $pre_j$ 表示 $i\to j$ 经过 $k$ 条边的路径上 $j$ 的前驱），所以我们就不需要枚举了。

没听懂？你在下面还会看到这道题的另一种解法。
[USACO09DEC] Cow Toll Paths G 我们只需要路径点权最大值，直接 floyd 不好做，因为你找不到路径点权最大值。

但是我们 floyd 是一点点往最短路加点，所以我们把节点按从小到大排序，这样我们保证每一次转移时路径点权最大值一定为 $i,j,k$ 中的一个，贡献就可以计算了。

同余最短路

和差分约束类似，最短路

dis_u+w\ge dis_v

的式子形式可以用在很多地方。

比如我们现在有一个方程

ax+by+cz=d

，

a,b,c\ge0

，求有多少个

d\in[0,V]

里的整数满足方程。

我们设

f(i)

表示满足

ax+by\equiv i\pmod c

的最小

ax+by

，容易发现，

f(i)

加上若干个

c

都可以满足该式子，我们只要计算

f(i)

有多少个倍数小于等于

V

即可，并且因为我们按余数分了类，一定不会计算重复。

如何计算

f(i)

？发现其满足如下式子：

\begin{aligned} f(i)+a\ge f((i+a)\bmod c)\\ f(i)+b\ge f((i+b)\bmod c) \end{aligned}

这个形式已经不用我再多说了，直接建图，显然

f(0)=0

，直接从

0

开始跑最短路即可求出

f(i)

。

模板：跳楼机

~~没有其他题目因为我再也没遇到过。~~

CPP

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int maxn = 1e5+30;
ll h,x,y,z;
vector<pair<int,ll>> e[maxn];
ll dis[maxn];bool f[maxn];
struct node{
    int p;ll w;
    bool operator < (const node &y) const {
        return w > y.w;
    }
};
priority_queue<node> q;
inline void dijkstra() {
    for (int i = 0; i < x; i++) dis[i] = LONG_LONG_MAX;
    memset(f,0,sizeof(f));
    dis[0] = 0;
    q.push({0,0ll});
    while (!q.empty()) {
        node t = q.top();
        q.pop();
        if (f[t.p]) continue;
        f[t.p] = true;
        for (auto i : e[t.p]) {
            ll v = i.first,w = i.second;
            if (dis[v] > dis[t.p] + w) {
                dis[v] = dis[t.p] + w;
                q.push({(int)v,dis[v]});
            }
        }
    }
}
int main() {
#ifdef LOCAL
    freopen("E:/codes/exe/a.in","r",stdin);
    freopen("E:/codes/exe/a.out","w",stdout);
#endif
    cin >> h >> x >> y >> z;
    --h;
    if (x > y) swap(x,y);
    if (y > z) swap(y,z);
    if (x > y) swap(x,y);
    assert(x<=y&&y<=z);
    for (int i = 0; i < x; i++) {
        e[i].push_back({(i+y)%x,y});
        e[i].push_back({(i+z)%x,z});
    }
    dijkstra();
    ll ans = 0;
    for (int i = 0; i < x; i++) {
        if (h >= dis[i]) ans += (h-dis[i])/x+1;
    }
    cout << ans << '\n';
    return 0;
}

和其他算法的配合

这里默认你会下面的算法，所以不对算法做介绍，也不做详细的思路讲解，就当作相关题目吧。

分数规划

[USACO07DEC] Sightseeing Cows G
[USACO19DEC] Milk Pumping G ~~好像不是分数规划。不管了反正题目不错做就行了。~~
最小密度路径我又回来了，仔细思考贡献和 01 分数规划形式一样，那我们二分做就行。

DS 优化建边

[CF786B] Legacy 线段树优化建图后最短路板子。
[XR-1] 逛森林无脑树剖线段树优化建边，时间复杂度 $O(n\log ^3 n)$ 显然不可行。正解并不好写，最短路里的重边不影响答案的（废话），所以这种可重复贡献你想到什么？
[JOIST 2023] 护照 / Passport 认真分析车站的可达性性质，同时一定记住最短路可以拼接。

其他算法杂项

[2025牛客暑期多校训练营2] H.Highway Upgrade/高速公路升级付费题目，如果你能看到的话可以看看。最短路可以拼接，永远不要忘了。最后想想你最优解的形式是什么可以怎么求。
[NOI2018] 归程知名卡 SPFA 题目。想想一个点可以步行到达的前提是什么？这个东西是不是能用个啥维护？

最短路树的性质

不给题解思路，给了好像就没啥意思了。

建模

不给思路，理由同上。

浅谈最短路常见应用

文章操作

板子