专栏文章

题解：P1919 【模板】高精度乘法 | A*B Problem 升级版

SSunrise_beforeglow
P1919题解参与者 9已保存评论 13

文章操作

快速查看文章及其快照的属性，并进行相关操作。

当前评论
12 条
当前快照
1 份
快照标识符
@mip6rygt
此快照首次捕获于
2025/12/03 07:05
3 个月前
此快照最后确认于
2025/12/03 07:05
3 个月前
查看原文

了解 FFT

由于本人是 xxs，数学学的不多，还请多多谅解。

前情提要

我们都知道，高中数学有一个叫做复数的东西。
虚数单位 ii 其实就是用来表示 x2=−1x^2=-1 的根。
为什么一定要弄一个这个东西呢，因为我们知道平方具有非负性，但虚数不一样，i2=−1i^2=-1，也就是 i=−1i=\sqrt{-1}。
那么复数，其实就是 a+bia+bi 的形式，其中 a,b∈Ra,b\in \mathbb{R}。
然后这个东西的加减乘除并不复杂，它也满足结合律，所以可以直接使用乘法、加法结合律计算，比如 (a+bi)(c+di)=ac+i2bd+i(ad+bc)=ac−bd+i(ad+bc)(a+bi)(c+di)=ac+i^2bd+i(ad+bc)=ac-bd+i(ad+bc)。
这个复数在编程中可以手写，也可以使用 STL 中的 complex 项。
这里我放上自己手写的：
CPP
struct node
{
    double x,y;
    node operator +(const node &g)const{return {g.x+x,g.y+y};}
    node operator -(const node &g)const{return {x-g.x,y-g.y};}
    node operator *(const node &g)const{return {g.x*x-g.y*y,g.x*y+g.y*x};}
};
那么我们其实可以将它一一映射到平面直角坐标系上，其中 a+bia+bi 在坐标系上可以唯一表示为点 (a,b)(a,b)。
我们再在坐标系上画出一个单位圆，它的方程为 (x−0)2+(y−0)2=1(x-0)^2+(y-0)^2=1，意思是所有 (x,y)(x,y) 满足与 (0,0)(0,0) 距离为 11 的点。
那么了解 FFT 之前，我们需要知道 nn 次单位根，我们定义 ωn1\omega_n^1 为方程 xn=1x^n=1 的根。
那么所有的根分别为 ωn0,ωn1⋯ωnn−1\omega_n^0,\omega_n^1\cdots \omega_{n}^{n-1}。
这几个数的复数表示分别为 1,cos⁡(2πn)+isin⁡(2πn)⋯cos⁡((n−1)2πn)+isin⁡((n−1)2πn)1,\cos(\dfrac{2\pi}{n})+i\sin(\dfrac{2\pi}{n})\cdots \cos((n-1)\dfrac{2\pi}{n})+i\sin((n-1)\dfrac{2\pi}{n})，也就是把单位圆平均分成 nn 份。
大概的示意图就是这样：
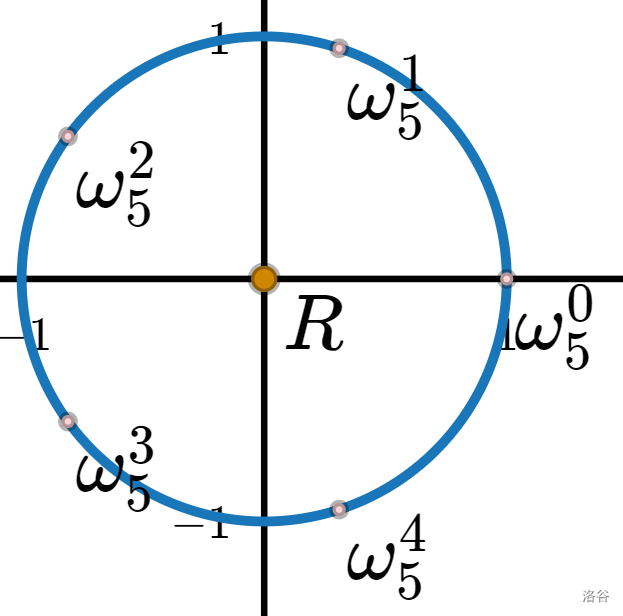
我知道你们有很多疑问，让我们一个个解决。
为了方便，令 α=2πn\alpha=\dfrac{2\pi}{n}。
首先我们需要知道单位圆的参数方程：
{x=cos⁡αy=sin⁡α\begin{cases} x=\cos\alpha\\ y=\sin\alpha \end{cases}
这个很好证，把这个带入单位圆的方程即可，意思是从 xx 轴开始，在单位圆上逆时针转 α\alpha 度。
所以这 nn 个根都在单位圆上。
接下来，我们需要知道，当我们已经定义 wn1=cos⁡α+isin⁡αw_n^1=\cos\alpha +i\sin \alpha 时，为什么 wnx=cos⁡xα+isin⁡xαw_n^x=\cos x\alpha+i\sin x\alpha。
我们可以使用归纳法证明：
  • 当 x=1x=1 时，显然成立。
  • 假设 x=k−1x=k-1 时成立，那么 x=kx=k 时。
wnk=wnk−1×wn1=(cos⁡(k−1)α+isin⁡(k−1)α)(cos⁡α+isin⁡α)w_n^k=w_n^{k-1}\times w_n^1=(\cos(k-1)\alpha+i\sin(k-1)\alpha)(\cos \alpha +i\sin \alpha)
=cos⁡kα+isin⁡kα=\cos k\alpha+i\sin k\alpha
所以，(wni)n=wnni=cos⁡2πi+isin⁡2πi=1(w_n^i)^n=w_n^{ni}=\cos2\pi i+i\sin2\pi i=1。
于是 wn0,wn1⋯wnn−1w_n^0,w_n^1\cdots w_n^{n-1} 为方程 xn=1x^n=1 的 nn 个复数根。
于是，从几何意义上看，我们知道了 ω2nk=−ω2nk+n\omega_{2n}^k=-\omega_{2n}^{k+n}。
我们还要了解多项式。
什么是多项式，我们定义一个 nn 次多项式 f(x)=an−1xn−1⋯a0x0=∑i=0n−1aixif(x)=a_{n-1}x^{n-1}\cdots a_0x_0=\sum\limits_{i=0}^{n-1}a_ix^i。
那么求 f(x)f(x) 的值，就是把 xx 代入这个多项式。
我们也可以使用 (x0,y0)⋯(xn−1,yn−1)(x_0,y_0)\cdots (x_{n-1},y_{n-1}) 这 nn 个点来唯一确定这个多项式，毕竟这 nn 个方程可以唯一确定这 nn 个系数。

正片开始

FFT，其实就是把系数表示法转换为点值表示法，再转换为系数表示法，进而加速多项式运算的过程。

FFT 正变换

我们可以做如下变换：
∑i=0n−1aixi=∑i=0n2−1a2ix2i+x∑i=0n2−1a2ix2i\sum_{i=0}^{n-1}a_ix^i=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}x^{2i}+x\sum_{i=0}^{\frac{n}{2}-1}a_{2i}x^{2i}
然后我们令 F(x)=∑i=0n2−1a2ix2i,G(x)=∑i=0n2−1a2ix2iF(x)=\sum\limits_{i=0}^{\frac{n}{2}-1}a_{2i}x^{2i},G(x)=\sum\limits_{i=0}^{\frac{n}{2}-1}a_{2i}x^{2i} 不难发现它们均为偶函数。
所以 f(ωnk)=F(ωnk)+ωnkG(ωnk)f(\omega_n^k)=F(\omega_n^k)+\omega_n^kG(\omega_n^k)。
f(ωnk+n2)=F(ωnk)−ωnkG(ωnk)f(\omega_n^{k+\frac{n}{2}})=F(\omega_n^k)-\omega_n^kG(\omega_n^k)。
也就是说，我们只要递归求解 F(ωnk)F(\omega_n^k) 与 G(ωnk)G(\omega_n^k) 的值，就可以知道 f(ωnk)f(\omega_n^k) 与 f(ωnk+n2)f(\omega_n^{k+\frac{n}{2}}) 的值。将它转化为点值表示法。
那么时间复杂度是多少，我们发现，一共会递归 log⁡2n\log_2n 层，每层需要花 O(n)O(n) 的代价合并，所以总时间复杂度 O(nlog⁡2n)O(n\log_2n)。
然后我们发现由于总是出现 n2\dfrac{n}{2} 所以我们不妨把 nn 直接补成二的若干次方的形式。
然后我们如果要求 f(x)g(x)f(x)g(x) 的点值表示法，我们可以求出 f(ωni)f(\omega_n^i) 和 g(ωni)g(\omega_{n}^i) 表示的值，那么 f(x)g(x)f(x)g(x) 在 ωni\omega_{n}^i 对应的值为 f(ωni)g(ωni)f(\omega_n^i)g(\omega_{n}^i)。

FFT 逆变换

假设一个多项式 h(x)=∑i=0n−1aixih(x)=\sum\limits_{i=0}^{n-1}a_ix^i，现在我们已经知道了它的点值表示法 (ωn0,h(ωn0))⋯(ωnn−1,h(ωnn−1))(\omega_{n}^0,h(\omega_{n}^0))\cdots (\omega_{n}^{n-1},h(\omega_{n}^{n-1}))。
现在我们需要根据点值表示法反推系数表示法。
我们干一个很匪夷所思的事情。
我们把它的点值表示法看成系数表示法。
也就是定义 H(x)=∑i=0n−1xi(∑j=0n−1ajωnij)H(x)=\sum\limits_{i=0}^{n-1}x^i(\sum\limits_{j=0}^{n-1}a_j\omega_n^{ij})。
然后我们以 H(x)H(x) 做一次 FFT，只不过这一次单位根要换成 ωn−k\omega_n^{-k}。
那么接下来我们推一下 H(ωn−k)H(\omega_n^{-k})。
H(ωn−k)=∑i=0n−1ωn−ik(∑j=0n−1ajωnij)H(\omega_n^{-k})=\sum\limits_{i=0}^{n-1}\omega_n^{-ik}(\sum\limits_{j=0}^{n-1}a_j\omega_n^{ij})
=∑i=0n−1(∑j=0n−1ajωnijωn−ik)=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j\omega_n^{ij}\omega_n^{-ik})
=∑i=0n−1(ak+∑j=0,j≠kn−1ajωni(j−k))=\sum\limits_{i=0}^{n-1}(a_k+\sum\limits_{j=0,j\neq k}^{n-1}a_j\omega_n^{i(j-k)})
=nak+∑j=0,j≠kn−1ωnj−kaj∑i=0n−1ωni=na_k+\sum_{j=0,j\neq k}^{n-1}\omega_n^{j-k}a_j\sum_{i=0}^{n-1}\omega_{n}^i
又 ∑i=0n−1ωni=ωnn−ωn0ωn1−1=0\sum\limits_{i=0}^{n-1}\omega_n^i=\dfrac{\omega_n^n-\omega_n^0}{\omega_n^1-1}=0。
所以原式等于 nakna_k。
所以做一次 FFT 之后，把得到的系数除以 nn 即可，时间复杂度 O(nlog⁡2n)O(n\log_2n)。
CPP
//这里node是我自己写的一个复数项
void FFT(node y[],int x,int type)//系数，长度，正变换或逆变换
{
    if(x==1)return;//当只剩常数项，直接返回
    node u[x/2+1],v[x/2+1];//为了节省空间，保证每一层空间都是O(n)复杂度
    for(int i=0;i<x;i+=2)u[i/2]=y[i],v[i/2]=y[i+1];//装填系数
    FFT(u,x/2,type);
    FFT(v,x/2,type);
    node w={cos(2*PI*type/x),sin(2*PI*type/x)},W={1,0};//预处理单位根
    //W其实就是单位根的i次方
    for(int i=0;i<x/2;i++)
    {
        y[i]=u[i]+W*v[i];
        y[i+x/2]=u[i]-W*v[i];
        W=W*w;//每次让W乘上一个单位根，使次数+1
    }
}
空间复杂度 O(nlog⁡2n)O(n\log_2n)。
不过这个东西可以 AC 另一道模板题。

我们继续提高难度

我们发现，递归 FFT 的缺点就是常数太大。
递归的常数过于大了。
那有没有什么办法，使得我们不需要递归呢？
有的兄弟有的。这时候就要讲一下蝶形算法优化。
我们假设函数 f(n,a)f(n,a) 表示编号为 aa 的数最后经过 FFT 之后会变到哪里。
  1. 如果 a≡1(mod2)a\equiv 1\pmod 2。那么偶数项都会排到前面，所以 f(n,a)=2n−1+f(n2,⌊a2⌋)f(n,a)=2^{n-1}+f(\dfrac{n}{2},\lfloor\dfrac{a}{2}\rfloor)。
  2. 如果 2∣a2\mid a，那么它会排到前半列，所以 f(n,a)=f(n2，a2)f(n,a)=f(\dfrac{n}{2}，\dfrac{a}{2})。
设 n=2kn=2^k。
我们发现，如果把它看成二进制有 kk 位的数，那么如果这个数最低位有一，那么最后的顺序的最高位就有一。
这不是把这个二进制数直接翻转的结果吗！
比如我们举个栗子。
ω80,ω81,ω82,ω83,ω84,ω85,ω86,ω87\omega_8^0,\omega_8^1,\omega_8^2,\omega_8^3,\omega_8^4,\omega_8^5,\omega_8^6,\omega_8^7
变换一次：ω80,ω82,ω84,ω86∣ω81,ω83,ω85,ω87\omega_8^0,\omega_8^2,\omega_8^4,\omega_8^6|\omega_8^1,\omega_8^3,\omega_8^5,\omega_8^7。
变换两次：ω80,ω84∣ω82,ω86∣ω81,ω85∣ω83,ω87\omega_8^0,\omega_8^4|\omega_8^2,\omega_8^6|\omega_8^1,\omega_8^5|\omega_8^3,\omega_8^7。
变换最终结果：ω80∣ω84∣ω82∣ω86∣ω81∣ω85∣ω83∣ω87\omega_8^0|\omega_8^4|\omega_8^2|\omega_8^6|\omega_8^1|\omega_8^5|\omega_8^3|\omega_8^7。
只看次数：(000)2,(100)2,(010)2,(110)2,(001)2,(101)2,(011)2,(111)2(000)_2,(100)_2,(010)_2,(110)_2,(001)_2,(101)_2,(011)_2,(111)_2。
最终顺序：(000)2,(001)2,(010)2,(011)2,(100)2,(101)2,(110)2,(111)2(000)_2,(001)_2,(010)_2,(011)_2,(100)_2,(101)_2,(110)_2,(111)_2。
如何求解一个数翻转二进制位得到的数？
设它为 resires_i，那么 resi=resi÷2÷2+[2∤i]×2n−1res_i=res_{i\div 2}\div 2+[2\nmid i]\times 2^{n-1}。
什么意思？[2∤i][2\nmid i] 是指当 ii 为奇数时返回 11，否则返回 00。所以 [2∤i]×2n−1[2\nmid i]\times 2^{n-1} 就代表翻转之后 ii 的最高位。
resi÷2res_{i\div 2} 意思就是把 ii 的最低位去掉，然后翻转。但我们想要的是最高位空出来，所以再除以 22。
CPP
for(int i=0;i<x;i++)
{
    res[i]=res[i/2]/2;
    if(i&1)res[i]|=(x/2);
    if(i<res[i])swap(y[i],y[res[i]]);
}
那么为什么只有当 i<resii<res_i 的时候才会交换呢？
因为 resires_i 翻转之后是 ii，你要是 i>resii>res_i 的时候再交换一遍，那不换回去了吗？
于是我们就有了以下非递归版 FFT。
CPP
void FFT(node y[],int x,int type)
{
    for(int i=0;i<x;i++)
    {
        res[i]=res[i/2]/2;
        if(i&1)res[i]|=(x/2);
        if(i<res[i])swap(y[i],y[res[i]]);
    }
    for(int g=2;g<=x;g*=2)//枚举分割的区间长度
    {
        node w={cos(PI*2/g),type*sin(PI*2/g)};
        //这里利用三角函数的cos(-x)=cos(x),sin(-x)=-sin(x)
        for(int i=0;i<x;i+=g)//每次向前跳一个区间
        {
            node o={1,0};
            for(int j=i;j<i+g/2;j++,o=o*w)//用上一层的点值答案推这一层的点值
            {
                node l=y[j],r=y[j+g/2];
                //由于y[j],y[j+g/2]推的刚好是这一层的y[j],y[j+g/2]，所以可以优化空间
                y[j]=l+o*r;
                y[j+g/2]=l-o*r;
            }
        }
    }
    if(type==-1)//处理逆变换
    {
        for(int i=0;i<x;i++)
        {
            y[i].x/=x;
            y[i].y/=x;
        }
   }
}
两个大整数相乘可以看成两个系数为 10k10^k 的多项式相乘。
于是此题思路显而易见。

复杂度分析

我们发现，第一层循环花费 log⁡2n\log_2n 的时间。
第二三层循环相当于把整个序列遍历了一遍。
所以总时间复杂度 O(nlog⁡2n)O(n\log_2n)。
空间复杂度由于我们一直在用一个数组求解，所以总空间复杂度 O(n)O(n)。

code

CPP
#include <bits/stdc++.h>
using namespace std;
int n,m,res[3000005],len;
string u,v;
struct node
{
    double x,y;
    node operator +(const node &g)const{return {g.x+x,g.y+y};}
    node operator -(const node &g)const{return {x-g.x,y-g.y};}
    node operator *(const node &g)const{return {g.x*x-g.y*y,g.x*y+g.y*x};}
};
node a[3000005],b[3000005];
double PI=3.1415926535;
void FFT(node y[],int x,int type)
{
    for(int i=0;i<x;i++)
    {
        res[i]=res[i/2]/2;
        if(i&1)res[i]|=(x/2);
        if(i<res[i])swap(y[i],y[res[i]]);
    }
    for(int g=2;g<=x;g*=2)
    {
        node w={cos(PI*2/g),type*sin(PI*2/g)};
        for(int i=0;i<x;i+=g)
        {
            node o={1,0};
            for(int j=i;j<i+g/2;j++,o=o*w)
            {
                node l=y[j],r=y[j+g/2];
                y[j]=l+o*r;
                y[j+g/2]=l-o*r;
            }
        }
    }
    if(type==-1)
    {
        for(int i=0;i<x;i++)
        {
            y[i].x/=x;
            y[i].y/=x;
        }
   }
} 
int main()
{
    cin>>u>>v;
    n=u.size(),m=v.size();
    for(int i=n-1;i>=0;i--)a[n-1-i].x=u[i]-'0';
    for(int i=m-1;i>=0;i--)b[m-1-i].x=v[i]-'0';
    len=1;
    while(len<n+m)len*=2;
    FFT(a,len,1);
    FFT(b,len,1);
    for(int i=0;i<len;i++)a[i]=a[i]*b[i];
    FFT(a,len,-1);
    for(int i=0;i<len;i++)
    {
        int u=a[i].x+0.5;
        a[i+1].x+=u/10;
    }
    while((int)(a[len].x+0.5)<=0)len--;
    if(len==0)
    {
        cout<<0;
        return 0;
    }
    for(int i=len;i>=0;i--)
    {
        int u=a[i].x+0.5;
        cout<<u%10;
    }
    return 0;
}

几道例题

都是模板题：
【模板】高精度乘法 | A*B Problem 升级版。
【模板】多项式乘法（FFT）。

后记

感谢同学 _FastFT2013的文章赞助：link。麻烦关注他谢谢。

评论

共 13 条评论，欢迎与作者交流。

正在加载评论...