专栏文章
杂题选讲 做题记录
个人记录参与者 1已保存评论 0
文章操作
快速查看文章及其快照的属性,并进行相关操作。
- 当前评论
- 0 条
- 当前快照
- 1 份
- 快照标识符
- @minmnl63
- 此快照首次捕获于
- 2025/12/02 04:54 3 个月前
- 此快照最后确认于
- 2025/12/02 04:54 3 个月前
题目标题后不带任何符号的说明此题是完全独立思考通过。
题目标题后带 * 的说明此题是在获得提示后通过。
题目标题后带 ** 的说明此题是在观看题解后通过。
2025.10.10 杂题选讲
1. AT_joisc2018_c Tents**
可以注意到,若 有帐篷的话,若这一行和这一列都有另外一个则无解;若这一行或这一列有另一个,则该帐篷只有一种方向;否则方向有四种可能。
于是考虑设 表示有 行 列的答案。
现在考虑新加入第 行:
-
若加入这一行没有帐篷,则有转移 。
-
若加入这一行有一个帐篷,且该帐篷所在列没有帐篷,那么该帐篷所在列作为新的一列加入,则有 。
-
若加入这一行有一个帐篷,且该帐篷所在列有一个另外的帐篷,则考虑将另外的这个帐篷视为新的一行加入,则有转移:。
-
若加入这一行有两个帐篷,则有转移:。
综上时间复杂度 。
2. P10744 Modulo Permutations
注意到 后面接什么都可以,也就是填入两个序列。直接 dp 即可。
时间复杂度 。
3. P9461 众数 II
考虑 什么时候能替代 作为答案。发现所涉及的所有块的 ,并且最左边的块必须取 开头,最右边的块必须取 结尾。
直接列式子求就行了。
时间复杂度 。
4. P7457 The Bridge on the River Kawaii
发现 很小,这下直接枚举 即可。然后就是一个线段树分治+可撤销并查集即可。
时间复杂度 。
不过 大一点好像可以直接整体二分,可以做到 。
5. P5871 Inversion*
bro 你怎么绿了。
注意到一个极长单调下降子序列为一个完全图,那么该子序列里必须取刚好一个点。那么一个合法方案就是一个极长单调上升子序列。
于是直接 dp。
时间复杂度 。
6. P3363 Cool loves jiaoyi**
唉唉双指针还是不熟。
最小极差问题考虑双指针。判断合法就直接用树剖维护最大经过点的次数即可。
时间复杂度 。
7. P4350 Export Estimate
本题一大难点是读懂题。
发现对 操作时,其他所有点的度数都不会变,也就是原本度数为 的点操作完后仍然为 。所以最终的操作次数为图中度数为 的点的个数,但是有一种特殊情况就是整个连通块是一个单环,此时最终会剩一个点,用并查集特判一下。
剩余边数也跟成功操作次数有关,直接算出来即可。
时间复杂度 ,瓶颈在排序。
8. P7220 [JOISC 2020] 掃除**
顶级数据结构题。
做法比较多,这里只讲一种。
每个点 可以投射到斜面,得到一个线段 。
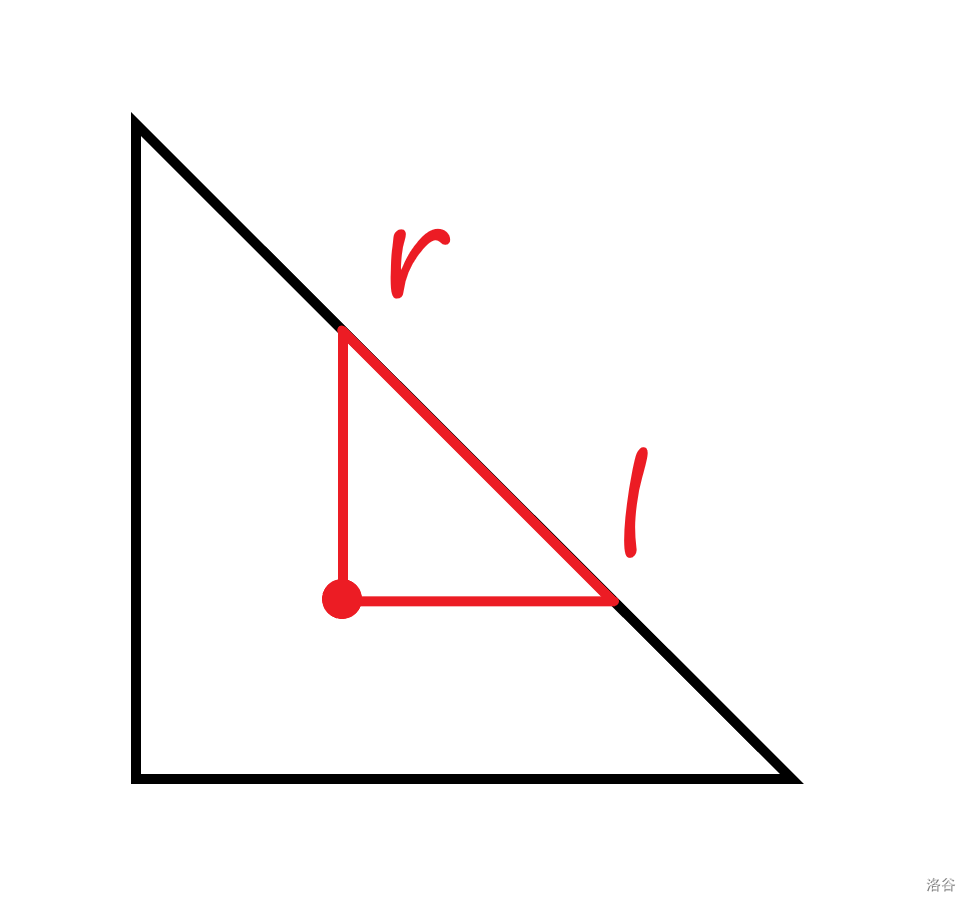 (图片来源 KobeBeanBryantCox 的题解,侵删)
(图片来源 KobeBeanBryantCox 的题解,侵删)那么每一次纵向操作 都是让所有满足 线段 执行 。
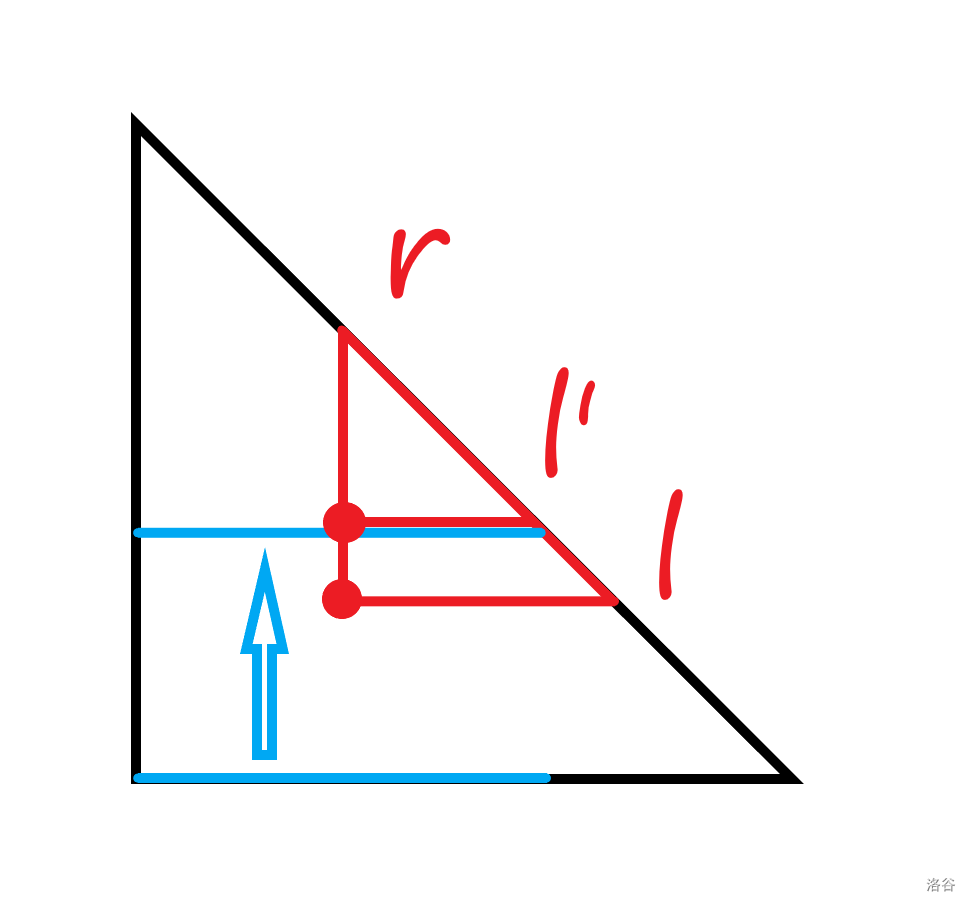
同理,每一次横向操作 都是让所有满足 的线段执行 。
那么如何维护这个操作呢?
考虑对于动态开点线段树上每一个点建一个容器。把每一个线段 放在满足 的深度最浅的节点上。
对整棵树执行 时,
- 若 ,则直接将该节点存的的所有线段的右端点 的全部赋值成 。
- 若 ,则将所有 的线段取出,暴力修改这些线段的右端点,然后暴力往下递归查找这个新线段该放到哪个节点上。因为树深度为 ,所以每个节点最多进行 次该操作。
执行 时同理。
于是考虑每个节点上用平衡树维护。此时发现每个线段的 可以分开存。因为需要,我们每个节点开两棵平衡树,一棵以 升序排序,一棵以 升序排序,同时还需支持区间赋值操作。这里直接用 fhq-treap 即可。那么暴力取出节点时,还需同时取出另一棵树上的对应节点。
那么总时间复杂度 ,支持在线。
9. P7324 表达式求值**
发现
? 是两边任取一边。首先根据序列构建出二叉树。然后直接 dp。
考虑对于每一个数 ,求出最终计算结果等于它的方案数。设 为当前节点为 ,且结果 小于/等于/大于 的方案数。
则当 的运算符为
> 时,则有:则当 的运算符为
< 时,则有:如果是
? 则把上面两种情况加起来。这样做是 。无法通过。
发现 很小,所以考虑 的做法。对于一个 ,设满足 的 集合 ,那么我们根据这个,同样列出 表示“小”的集合为 的方案数。
这样预处理的时间复杂度为 。
然后对于每一个 ,求出满足 的 构成的集合 ,求出 即为方案数。
这样做可能会被卡常,实际上只用记 表示 小于/大于等于 的方案数,然后再容斥一下即可。
时间复杂度 。
10. P7294 Minimum Cost Paths P*
设 为走到 的最小代价。
注意到 。
记录 。
那么 。而 。
只要维护出 即可,并支持整体加一个公差为 的数组,以及区间取 (但这里是单增的,所以可以改为区间赋值)。
不知道能不能用线段树,应该挺复杂的。
这里我用的二分+栈。栈里存的是取 时的断点。每一次取 可以根据当前时间戳和该断点的时间戳求出该点在此时的值,如果大于 则直接弹出,否则保留并对后面这个部分进行二分。
而 只需在同时维护一个前缀和即可快速计算。
时间复杂度 。
提交记录,最优解第一页!
相关推荐
评论
共 0 条评论,欢迎与作者交流。
正在加载评论...