题解：P9864 [POI 2021/2022 R2] age

Solution

直接根据原题意做是困难的，我们需要将其简化。

发现可以考虑哪些边只用走一次。考虑将关键点之间一一断开，每个关键点把自己的块走完。转化一下，就是：每个关键点向外延伸一条路径，路径不能相交，求最大路径长度和，最终答案就是

2(n-k)-M

，

M

是最大路径长度和。

考虑 dp。对于一个点是否出现在路径中，一共有

4

种状态：

作为一个单点（非关键点），不出现在任何路径中；
作为路径中的一个点，这条路径从子树中延伸过来，但这条路径还没有包含关键点；
作为路径中的一个点，这条路径从子树中延伸过来，这条路径已经包含关键点；
作为路径中的一个点，这条路径已经形成，即它从一棵子树中延伸过来，又从另一棵子树中走出去。

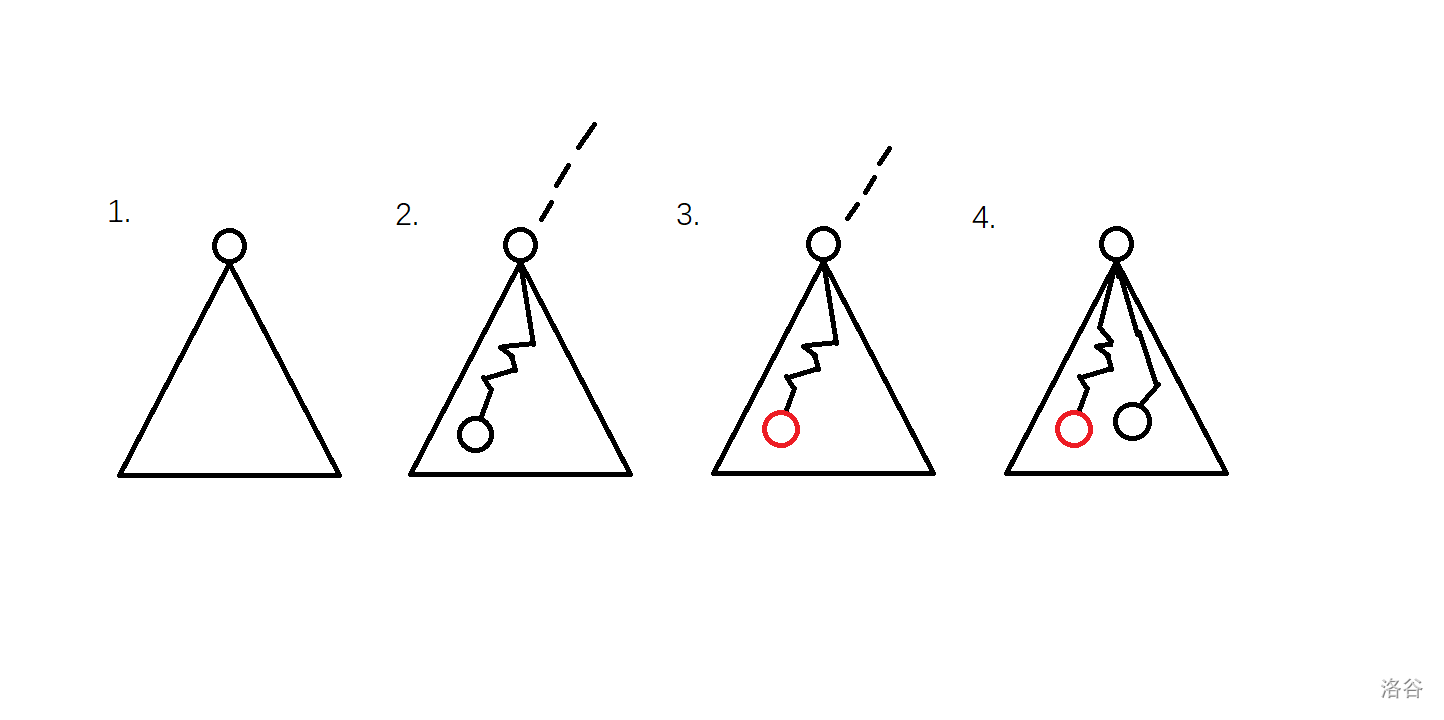
（三角形代表子树，红点为关键点，黑点为非关键点）

设计状态

f_{u,0/1/2/3}

表示在以点

u

为根节点的子树中，点

u

分别为

4

种状态时，关键点能延伸出的路径长度最大值。转移是显然的，枚举子树的时候根据情况转移即可。情况

4

根据情况

2,3

转移过来。细节可参考代码。

Code

CPP

#include<bits/stdc++.h>
using namespace std;
const int N = 500005;
int n,k,book[N],f[N][4];
vector<int>vec[N];
void dfs(int u,int fa)
{
	if (!book[u]) f[u][0] = f[u][1] = 0;
	else f[u][2] = f[u][3] = 0;
	for (int i: vec[u])
	{
		if (i == fa) continue;
		dfs(i,u);
		if (!book[u])
		{
			int mx = max(f[i][0],f[i][3]);
			f[u][3] = max({f[u][1]+f[i][2]+1,f[u][2]+f[i][1]+1,f[u][0]+f[i][2]+1,f[u][3]+mx});
			f[u][1] = max(f[u][0]+f[i][1]+1,f[u][1]+mx);
			f[u][2] = max(f[u][0]+f[i][2]+1,f[u][2]+mx);
			f[u][0] += max(0,mx);
		}
		else
		{
			f[u][3] = max(f[u][2]+f[i][1]+1,f[u][3]+max(f[i][0],f[i][3]));
			f[u][2] += max(f[i][0],f[i][3]);
		}
	//	cout << u << ' ' << f[u][3]+max(f[i][0],f[i][3]) << '\n';
	}
}
signed main()
{
	ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> k;
	for (int i = 1; i <= k; i++)
	{
		int a;
		cin >> a;
		book[a] = 1;
	}
	for (int i = 1; i < n; i++)
	{
		int u,v;
		cin >> u >> v;
		vec[u].push_back(v);
		vec[v].push_back(u);
	}
	memset(f,-0x3f,sizeof f);
	dfs(1,1);
	cout << (n-k)*2-max({f[1][0],f[1][2],f[1][3],0});
	return 0;
}

题解：P9864 [POI 2021/2022 R2] age

文章操作

Solution

Code

相关推荐

评论

题解：P9864 [POI 2021/2022 R2] age